
V idealiziranem modelu protitočnega toplotnega izmenjevalca se toplota prenaša iz vode v notranji cevi (na shemi teče v levo) v vodo v zunanji cevi. Tak sistem omogoči, da se v okolico izgubi veliko manj toplote kot bi se sicer.

Radi bi ugotovili kako se temperatura spreminja vzdolž notranje ali zunanje cevi. Ker voda v notranji cevi oddaja toploto po vsej dolžini, se ji temperatura spreminja, zaradi temperaturne razlike pa tudi toplotni tok. Ker se temperatura spreminja tudi po dolžini zunanje cevi, enačbe seveda še zdaleč niso linearne, zato bomo cev v mislih razrezali na zelo majhne odseke in opazovali, kaj se dogaja s toploto na posameznem odseku cevi.
Najprej napišemo enačbo za toplotni tok na dolžini x:
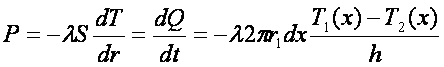
tu je T1 temperatura v notranji cevi, T2 pa v zunanji. Debelino stene predstavlja h. Zaradi tanke stene in lažjega računanja bomo predpostavili, da se površina prevajanja z debelino ne spreminja. Omeniti še velja, da λ predstavlja toplotno prevodnost snovi, iz katere je cev, r1 pa je polmer notranje cevi.
Majhno spremembo toplote bi lahko zapisali kot:
![]() ,
,
spremembo mase pa
![]() ,
,
tu je ρ gostota vode, v hitrost, indeks ena pa se nanaša na notranjo cev. Analogno enačbo bi lahko pisali za zunanjo cev, le da bi kot indeks uporabili 2. Kombinacijo zgornjih treh enačb predstavlja enačba
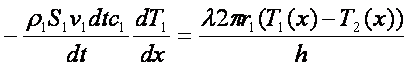
Zaradi ogromnega števila konstant v enačbi, si v želji po večji preglednosti enačbo poenostavimo v toliko, da vse nespremenljive količine označimo s črko k:
![]()
Črtica nad T1 pomeni, da gre za odvod ![]() .
.
Osnovna predpostavka naše izpeljave bo, upoštevši zakon o ohranitvi energije, da notranjo cev zapusti prav toliko toplote kot je pride v zunanjo. To zapišemo tako:
![]()
Da omogočimo kombiniranje obeh osnovnih enačb, moramo v drugi pridelati odvod, zato jo delimo z dx:
![]()
Kot prej pišemo tudi zdaj zmnožek konstant s črko k:
![]()
pri čemer je ![]() . Enačbi povežemo med sabo in dobimo:
. Enačbi povežemo med sabo in dobimo:
![]()
To je zapletena zveza, ki povezuje prvi in drugi odvod obeh temperatur. Zaradi lažjega reševanja bomo definirali novo količino z. Še malo potelovadimo:
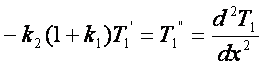
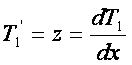
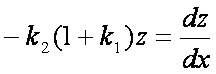
Zdaj je že vse nared za integriranje:
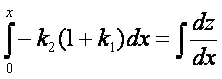
![]()
Ker ne poznamo mej integrala na desni strani enačbe, bomo izračunali nedoločni integral, konstanto c pa določili na koncu iz robnih pogojev. To pomeni, da bomo v končno enačbo vstavili podatke, ki jih poznamo in izračunali neznano količino.
Formula za z bi se po novem glasila:
![]() ,
,
oziroma
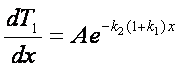
Za ta integral poznamo vse meje, zato ni težko izračunati končno odvisnost:
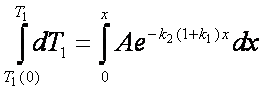
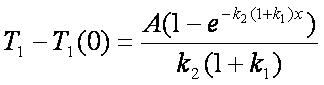
To je končna zveza med temperaturo v notranjem delu cevi in razdaljo. Čudna eksponentna odvisnost nam pravi, da stvari še daleč niso tako enostavne. Zaradi obilice približkov v izpeljavi (voda se po nekem preseku enako hitro segreva, toplotni tok je pravokoten na cev, popolna izolacija cevi,…) je vprašanje pod kakšnimi pogoji bi jo sploh lahko preverili v praksi.