Teoretično ozadje (enačbe potrebne za izračun):

Enačba parabole:

Y = k

Enačba parabole, kot bi bil npr. žleb, kjer bi se zaradi pospeška gibala kroglica. V našem primeru se giblje zračni mehurček v vodi.

Wp= m g y = m g k

F = = -m g k 2 x iz tega sledi:

m a = m g k 2 x ---> a = g k 2 x

Izračun koeficienta ukrivljenosti cevke:

y = k vstaviš točke merjene cevke.

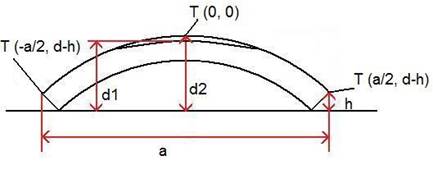
K = a je dolžina cevke, d je višina cevke in h višina do roba cevke, k je seveda koeficient ukrivljenosti cevke.

a = 101,4mm

h = 22,7mm

d = 36mm

S koeficientom ukrivljenosti smo nato računali pospešek:

a = 2 g k x

kjer je a centripetalni pospešek, g gravitacijski pospešek, k koeficient ukrivljenosti cevke in x odmik mehurčka pri iskanem pospešku.

Za preverjanje rezultatov smo izračunali še radialni pospešek iz hitrosti vrtenja in poznanega radija:

a = r kjer je a centripetalni pospešek, kotna hitrost in r radij merilca pospeška.

Kotne hitrosti s katerimi smo delali, so bile: γ= , γ= , γ= ;

Iz katerih smo dobili naslednje radialne pospeške: a₁=0,387, a₂=1,648, a₃=3,06