TEORIJA

Natega je postopek, pri katerem s cevjo prečrpavamo tekočino iz višje ležeče posode v nižjo ležečo posodo. Deluje na osnovi tega, da je v cevi neprekinjen stolpec tekočine, ki sega od ene posode do druge, skupaj pa ga držijo sile med delci tekočine. Tekočino v smeri nižje posode požene teža, ni potrebno nobeno dodatno poganjanje. Nujno pa je, da je izstopna odprtina cevi nižje od gladine vode v prvotnem zbiralniku.

Viri poročajo [1], da so natego uporabljali že stari Egipčani. Glede na to bi si mislili, da je natega zelo preprost pojav, ki bi ga vsak poučeni človek znal razložiti, kljub temu pa je še marsikje mogoče najti nasprotujoče si razlage njenega delovanja. Primeri takih razlag so navedeni v članku S. W. Hughesa [2], kjer so med drugim obravnavane tudi take, ki natego pojasnjujejo s tlačno razliko.

Natančen opis delovanja natege je lahko precej zapleten, ob predpostavki, da imamo opravka z idealnimi tekočinami pa jo lahko dokaj dobro opišemo z Bernoullijevo enačbo. Pri tej gre za pojav ohranitve mehanske energije, ki velja le, kadar tok ni turbulenten in tekočina ni niti stisljiva niti viskozna.

Za poljubno točko vzdolž takega toka velja Bernoullijeva enačba, pri kateri je p tlak, 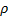gostota tekočine, g težni pospešek, h višina, 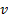hitrost tekočine:

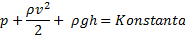
Z njo povežemo poljubni dve točki v toku, pri tem pa nam ni potrebno upoštevati same poti, ki jo tok med tema točkama opiše.

Najvišja možna višina najvišje točke cevi natege

Tudi v idealnih pogojih natega ne more delovati, če je kateri del cevi previsoko. Najvišjo višino, preko katere še lahko črpa, lahko izračunamo tako, da izračunamo višino, pri kateri je tlak v tekočini enak 0 - tukaj bi se tekočina gotovo uparila, stolpec tekočine pa pretrgal. Označimo: 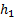iskana višina najvišjega dela cevi, 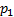tlak na višini 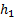in 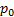zunanji tlak. V splošnem lahko dve točki vzdolž cevi povežemo z Bernoullijevo enačbo (količine enako označene kot prej, le z indeksoma 1 in 0 ločene za posamezni točki):

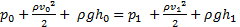
S količinami z indeksom 0 označimo točko na gladini posode, iz katere črpamo, z indeksom 1 pa količine točke v najvišjem delu cevi. Predpostavimo, da črpamo iz velikega rezervoarja, v katerem se gladina zanemarljivo počasi giblje (začetna hitrost je 0), višino pa postavimo na 0 pri gladini tega rezervoarja. Na najvišji točki zanemarimo hitrost vode. Tlak 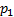je po naši predpostavki enak nič.

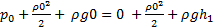
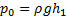
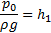
Tako smo dobili najvišjo možno višino nad gladino višjega rezervoarja, preko katere natega še lahko črpa (idealno) tekočino. Če vstavimo v prejšnjo formulo zunanji tlak (100 kPa) in gostoto (1 kg/L) vode dobimo najvišjo višino približno 10 m. Rezultat potrjuje tudi Wikipedija [1].

Pravzaprav je možno, da natega deluje tudi preko večje višine od izračunane. To je posledica pojava, ki ga imenujemo kohezija [3] – zaradi vezi med molekulami lahko voda prenese tudi tlake manjše od 0. To pomeni, da jo lahko do določene mere tudi raztegujemo in bo še vedno ostala v kapljevinasti obliki. Negativni tlak, ki ga voda še prenese je med drugim odvisen tudi od širine cevi, po kateri se voda pretaka.

Pri našem poskusu smo uporabljali dokaj velike preseke cevi, zato ta pojav verjetno ne bi bil opazen. Precej pomemben pa je pri manjših presekih, na primer pri žilah dreves. Kohezija vode pravzaprav omogoča drevesom, da dosežejo višino nekaj deset metrov in več, voda pa se po njih pretaka le s pasivnim transportom.

Hitrost iztekanja v odvisnosti od višinske razlike

Zanimiv podatek je hitrost tekočine, ko izteka iz cevi. Izpeljava enačbe za idealne tekočine je sledeča, izenačimo Bernoullijevi enačbi za točko na gladini rezervoarja iz katerega črpamo (indeksi 0), ter ob ustju cevi, kjer tekočina izteka (indeksi 1):

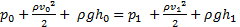
Vzemimo ničlo višine ob gladini rezervoarja ter višino ustja cevi, pri katerem tekočina izteka, za negativno. Spet predpostavimo, da je hitrost tekočine ob gladini zanemarljiva. Obe točki sta pri zunanjem tlaku in imata zato enaka tlaka.

Iz tega sledi:

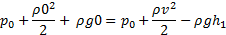
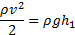
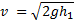
Realna tekočina

Za realne tekočine je Bernoullijeva enačba dobra le za oceno. Najprej je treba vedeti, ali je tok v cevi laminaren ali turbulenten. Za to obstaja kriterij, ki se imenuje Reynoldsovo število, kjer je v hitrost tekočine, d premer cevi, 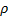gostota tekočine, 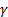gama viskoznost tekočine.

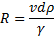
Če je Reynoldsovo število večje od 3000, potem je tok turbulenten, če je manjše od 2000 pa laminaren [4]. Med 3000 in 2000 pa običajno ne vemo, kar je potrebno ugotoviti s poskusi. Za boljši približek je treba upoštevati še stiskanje vode, ki je posledica sprememb tlaka v cevi, … Več popravkov kot upoštevamo, bolj točen rezultat dobimo.

Popravki za turbulentni tok

Če imamo v cevi turbulentne tokove in želimo izračunati hitrost vode, moramo upoštevati naslednji popravek. Izgube zaradi turbulentnega toka lahko predstavimo z namišljenim zmanjšanjem višinske razlike h, ki poganja natego, za 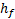[5].

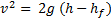
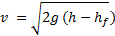
Pri tem lahko zmanjšanje višinske razlike 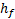izračunamo z Darcyjevo enačbo [5]:

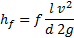
Kjer je f koeficient trenja tekočine s steno cevi, l dolžina cevi, v hitrost tekočine v cevi, d premer cevi, g težni pospešek. Iz Blasiusove empirične enačbe [5] lahko dobimo f:

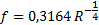
ki pa velja samo, če je Reynoldsovo število med 3000 in 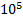10na5 .

Če Darcyjevo enačbo vstavimo v popravljeno enačbo za hitrost dobimo:

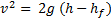
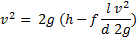
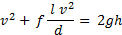
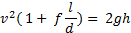
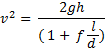
Obstajajo tudi aproksimacije, ki opišejo izgube zaradi oblike cevi - motenj, kot so na primer ostri zavoji, stiki različnih cevi ipd. - pri čemer si pomagamo s tabelami. Pripišemo jim še dodatno zmanjšanje višinske razlike, ki poganja natego, 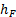hff . To kar dodatno prištejemo zmanjšanju te količine zaradi popravkov za turbulentni tok [5]. Vsaki motnji moramo empirično določiti brezdimenzijski koeficient k:

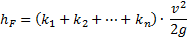
Kakor pri popravku za turbulentni tok, vstavimo to v popravljeno enačbo za hitrost iztekanja, ki izgube predstavi z namišljenim zmanjšanjem višinske razlike. Sledeča enačba sedaj upošteva tako izgube zaradi turbulentnega toka, kot tudi zaradi motenj v obliki cevi (oznake količin so nespremenjene):

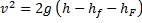
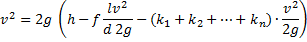
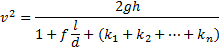
Korenimo to enačbo, pomnožimo jo še s presekom cevi S in dobimo izraz za volumski pretok :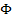

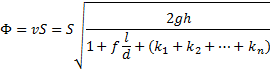
Predpostavimo, da je vseh motenj v cevi N in so vse enake oblike (npr. N zaporednih zavojev enakega premera). Vsem motnjam pripišimo enak koeficient k:

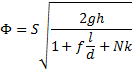
Ravnokar dobljeno zvezo smo skušali preveriti s poskusom, v razdelku Meritve smo zato meritvam prilagajali sledečo funkcijo s parametroma C in k:

Na vrh strani