Nevidna steklenica
Odvisnost ugasnitve sveče od pretoka zraka
Jakob Jerič, Mihael Haule, Vid Karčnik, Samo Bergant
Mentorica: doc. dr. Andreja Šarlah
Projektna naloga
Gorečo svečo postavite za steklenico. Če pihate v steklenico z nasprotne strani, sveča lahko ugasne, kot bi vmes ne bi bilo steklenice. Raziščite, od česa in kako je odvisen uspeh pihanja, ter razložite pojav. Predlagano razlago testirajte z dodatnimi poskusi.
S poskusi, opravljenimi pri predmetu Projektno delo II, smo poskušali razložiti, kakšen vpliv ima ovira na pogasitev sveče, ter kako se na splošno zrak giblje okoli preprostih ovir. Gre za opazovalni poskus, ki vrne pretežno kvalitativne rezultate. V primerjavo z meritvami pa smo naredili tudi simulacijo, ki lepše prikaže dogajanje med delom poskusa, ki se ukvarja s tokom zraka.
Opis poskusa
Oprema
Tekom izvajanja poskusov smo uporabljali dva valja. Večji valj s premerom , smo uporabljali v vseh treh poskusih. Manjši valj s premerom , pa smo uporabljali zgolj v drugem poskusu. Za izvor vetra smo uporabili ventilator, ki je ustvarjal hitrosti vetra pred valjem. Za zajemanje hitrosti vetra smo uporabljali anemometer.
Prvi poskus
Ventilator, pokončen valj in svečo smo postavili na isto os. Prižgali smo svečo, nato pa še ventilator in le tega začeli počasi približevati valju. Ko je sveče ugasnila, smo zabeležili razdalje ventilator-valj in valj-sveča in pri isti postavitvi izmerili hitrost zraka na mestu plamena v smeri vzdolžne osi . Vsako postavitev smo ponovili trikrat. Opazili smo, da je pri večji oddaljenosti sveče od valja, razdalja ventilator-valj manjša, hitrost zraka na mestu ugaslega plamena pa višja. To nas je presenetilo, ker smo pričakovali, da bo ta hitrost konstantna, zato smo posvetili celoten projekt k odkrivanju, zakaj se to zgodi. Merjenje hitrosti vetra vzdolž osi, pri postavitvi, pri kateri je ugasnila sveča
Merjenje hitrosti vetra vzdolž osi, pri postavitvi, pri kateri je ugasnila sveča
Drugi poskus
Da bi boljše razumeli prejšnjo odvisnost, smo želeli odkriti, kakšne so tokovnice zraka za valjem. Prva ideja je bila, da posnamemo, kako se majhni delci premikajo zaradi vetra. Najprej smo ustvarili vodno paro tik za ventilatorjem, vendar je nismo mogli ustvariti dovolj, da bi jasno videli tokovnice. Nato smo dodali laser in ga usmerili prečno na os, na drugo stran zračnega toka pa postavili črno pobarvan karton, da bi povečali kontrast. Hitro smo ugotovili, da še vedno nimamo dovolj pare in naše kamere nimajo dovolj dobre resolucije, da bi lahko posnele posamezne tokovnice. Tretjič smo poskusili z magnezijevim oksidom, toda delci so bili pretežki, da bi jih veter, ki ga je ustvaril naš ventilator, lahko dovolj premikal.
Odločili smo se, da izmerimo komponente hitrosti v smeri osi in pravokotno na os , tako da dobimo skalarno polje hitrosti in približek tokovnic. Skalarno in ne vektorsko polje pa zato, ker je naš anemometer lahko meril le velikost hitrosti glede na usmerjenost. Ugotovili smo, da so komponente enake na mestih, prezrcaljenih preko osi .
Poskus z zajemanjem tokovnic s pomočjo pareTretji poskus
Ponovili smo prvi poskus, toda tokrat, smo merili hitrosti v smeri osi in , nad svečko na oddaljenost ventilatorja, pri kateri je sveča ugasnila. Zanimalo nas je, ali je za prvotno opažene spremembe hitrosti na osi, pri katerih sveča ugasne, odgovorna sprememba hitrosti na osi. Prav tako pa nas je zanimalo če in kako se spreminja "skupna" hitrost .
Analiza poskusa
Zaradi preprostih in nenatančnih meritev je za nas pomembna predvsem kvalitativna slika dogajanja, saj lahko tako grobo ocenimo, kaj bi lahko pričakovali v podobnih poskusih.
Prvi poskus
Na začetku smo želeli videti pri kateri razdalji in hitrosti sveča ugasne, če ni ovire med ventilatorjem in svečo. Tabela 1 prikazuje štiri meritve razdalj in ustreznih hitrosti, pri katerih sveča ugasne. Relativna napaka obeh meritev je reda velikosti . Napaka pri prikazuje spremembo hitrosti med zajemanjem ene meritve, pa je bila konstantna med zajemanjem meritve. Napaka pri pa je zaradi uporabe merilnega traka.
| Tabela 1: Hitrosti, pri katerih ugasne svečka brez valja |
|---|
| | |
|---|
| | |
| | |
| | |
| | |
 Tloris prvega poskusa brez valja
Tloris prvega poskusa brez valjaKot povedano v opisu poskusov, smo pri prvem merjenju merili le komponente hitrosti .
Zanimala nas je odvisnost razdalje ventilator-valj () glede na razdaljo valj-sveča (), ko je ventilator na razdalji, pri kateri sveča ugasne. Kot oviro smo uporabili večji steklen valj. Večji kot je , večji je . Več o te odvisnosti ne moremo povedati, saj imamo premalo meritev s preveliko negotovostjo, da bi lahko naredili uporabno napoved. Odvistnost prikazuje graf 1.
Pri merjenju smo prav tako opazili spreminjanje , pri kateri je sveča ugasnila, v odvisnosti od razdalje , ki je predstavljena na grafu 2. Različne hitrosti so nas presenetile, saj smo intuitivno pričakovali, da bo sveča ugasnila pri enakem hlajenju in posledično pri enaki hitrosti. Ker je bil dotok zraka in s tem kisika zadosten, sveča pa še ni bila močno rabljena in naj bi torej imela še dovolj goriva, smo si razložili, da je za pogasitev pri različnih hitrostih kriva konvekcija. Da bi preverili, če je ta razlaga pravilna, smo z nadaljnimi poskusi želeli natančneje izmeriti dejanske velikosti hitrosti toka zraka nad stenjem sveče. Tloris prvega poskusa z valjem
Tloris prvega poskusa z valjem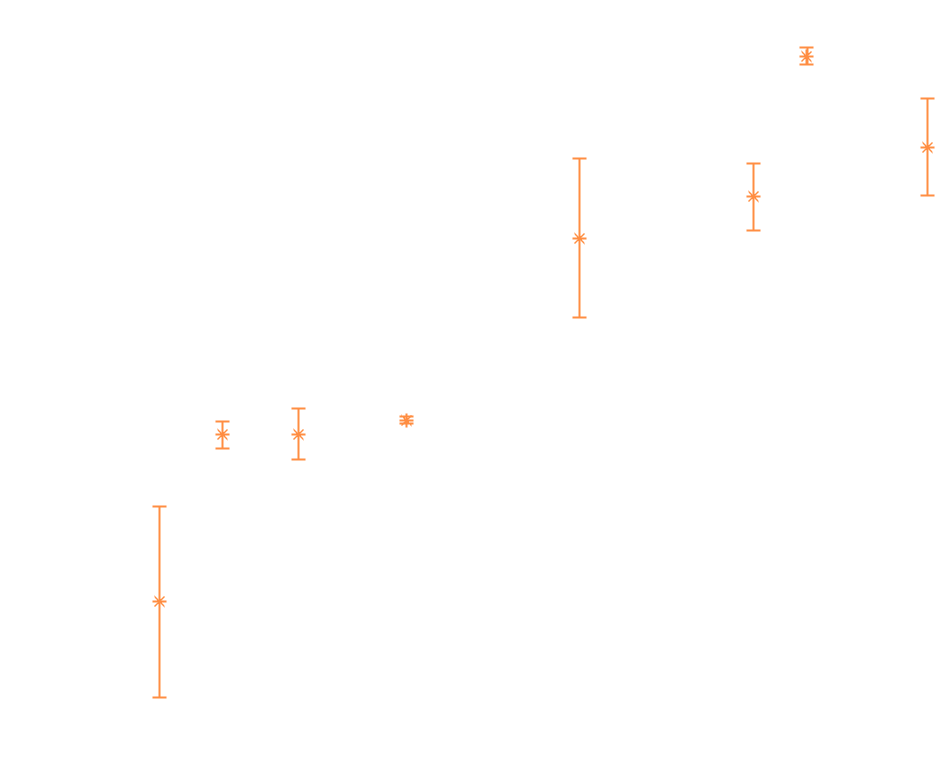 Graf 1
Graf 1 Graf 2
Graf 2
Drugi poskus
Zanimalo nas je, kakšen je hitrostni profil zraka za oviro. Iz polja 1 razberemo, da najverjetneje obstajajo vrtnci okoli točke , ker so tam večje od . Do vrtincev pride, ker poskuša zrak zaobjeti oviro, česar pa zaradi visokega Reynoldsovega števila ne naredi laminarno temveč turbulentno. Pri našem poskusu je namreč Reynoldsovo število približno . Razlog, da ne moremo biti prepričani o obstoju vrtincev pa je, da anemometer poda skalarno vrednost in posledično ne vemo smeri hitrosti. Na srečo lahko sklepamo vsaj iz usmeritve anemometra, če predvsem zajema tokove v smeri ali osi. Vidimo, da so hitrosti simetrične preko osi. Prav tako lahko iz polja 1 vidimo, da v splošnem hitrosti padajo z oddaljenostjo od ovire. Do tega pride, zaradi viskoznosti, ki je disipativna sila, zračni tok izgublja energijo. Tik za oviro hitrost zraka močno pade. Ker je tam posledično tlak nižji, se tokovnice začnejo ukrivljati navznoter in za oviro dobimo vrtince. Iz polja 1 in polja 2 opazimo, da v nasprotju z manjšanjem , se povečuje. To opažanje nam je dalo idejo, da se iz prvega poskusa spreminja, ker se hkrati spreminja obratno. Iz polja 3, kjer je skalarna vrednost vidimo, da se manj spreminja kot v odvisnosti od razdalje od valja, kar najverjetneje pomeni, da je naša razlaga, o spremembi pri prvem poskusu zaradi konvekcije, vsaj delna razlaga. Tloris drugega poskusa
Tloris drugega poskusa
Tudi za manjši valj dobimo podobne, a zaradi majhne ovire manj očitne rezultate. Predstavljeni so v polju 4, 5, 6. Rezultati so takšni tudi zato, ker so razmiki med točkami, v katere smo postavili anemometer, relativno na velikost ovire večji, kot pri prvi meritvi. Posledično dobimo manjšo delitev pomerjenega prostora. Da ima ovira manjši prečni presek, lahko vidimo iz polja 5, saj tokovnice lažje pridejo tik za njo in je prečna hitrost zato že takoj po valju visoka. Poleg tega je hitrostna luknja za oviro manj široka, kot pri večjem valju.
Tretji poskus
Da bi testirali razlago iz 1. poskusa, da je vzrok za spremembo konvekcija, smo dodali meritve hitrosti tudi po osi . To še vedno ne da zelo natančnega rezultata. Tudi te meritve, predstavljene na grafu 3, kažejo na rast hitrosti, potrebne za pogasitev plamena pri oddaljenosti sveče od valja. Glede na majhno število izmerkov in njihovo nenatančnost pa to težko vzamemo za dejstvo. Na grafu 4 se vidi, da so meritve hitrosti in , pri katerih ugasne sveča, drugačne kot hitrosti na polju 1, 2 v istih točkah. Vzrok za to razliko mora biti premikanje ventilatorja in sama prisotnost sveče, ker sta to edini razliki v izvajanju drugega in tretjega poskusa. Poleg tega nismo uspeli dovolj natančno upoštevati dejstva, da daljši čas hlajenja in različne hitrosti premikanja izvora ter s tem začetne hitrosti vetra, prav tako botruje k drugačnemu hlajenju goriva.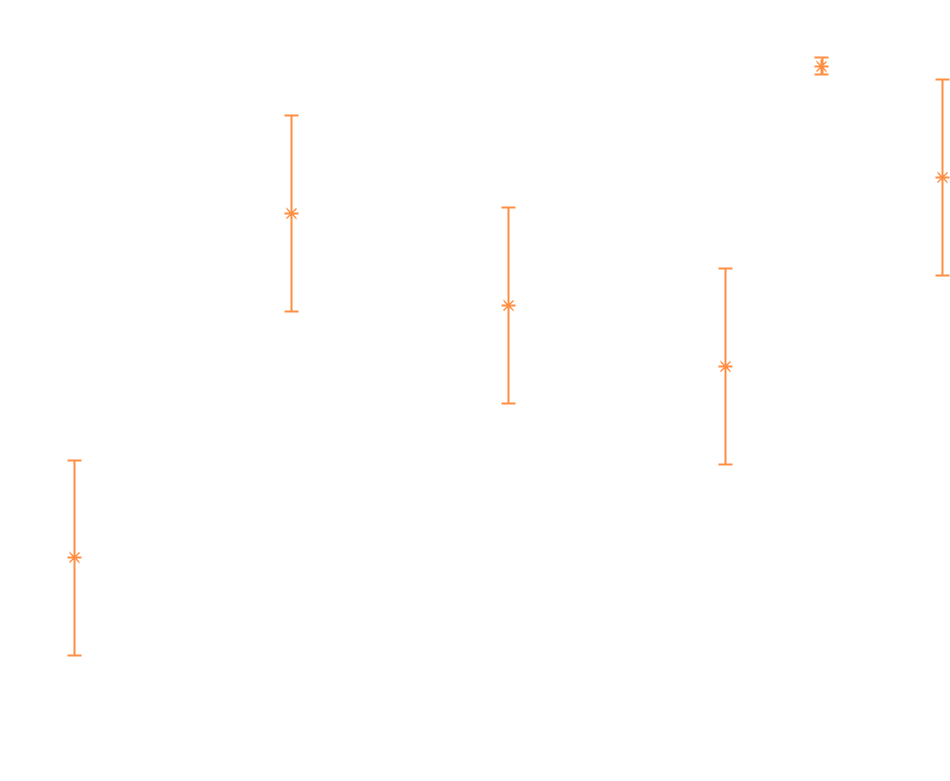 Graf 3
Graf 3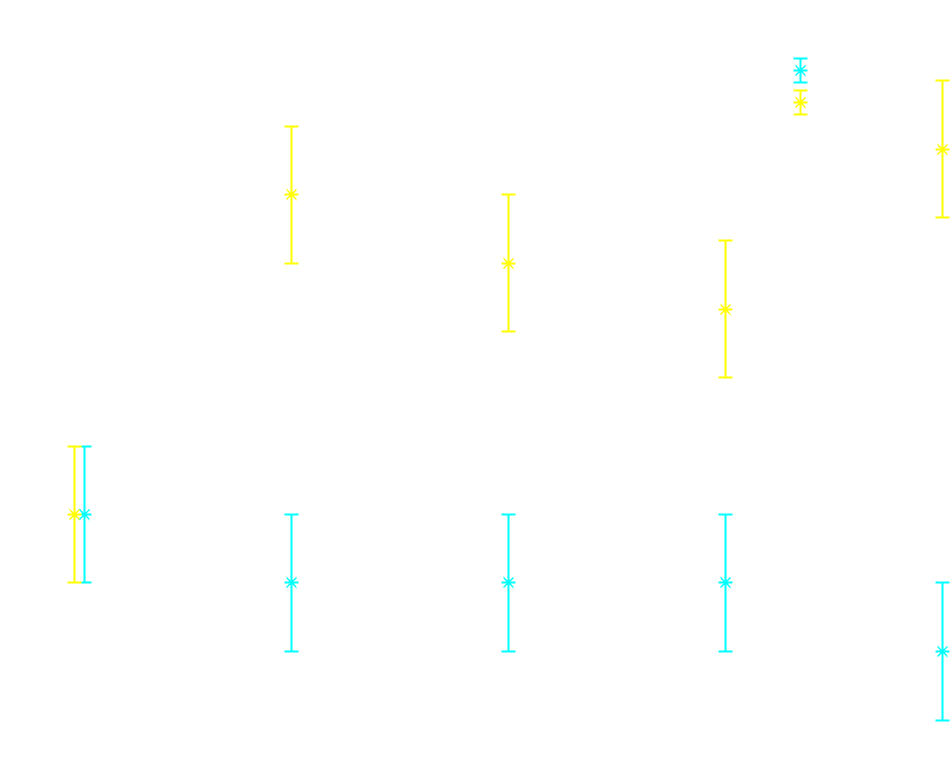 Graf 4
Graf 4
Negotovosti in izboljšave
V vseh treh poskusih smo pri meritvah naleteli na težave, ki so nam zaradi negotovosti meritev onemogočile, da bi lahko nalogo obravnavali kvantitativno, kot smo si želeli. Nekatere negotovosti izhajajo že iz same narave našega projekta. Namreč pri merjenju turbulentnega toka ne moremo pričakovati konstantne velikosti posameznih komponent hitrosti. Za izboljšavo slednjega, bi lahko hitrost vetra merili z boljšim merilnikom. Če bi merilnik lahko povezali z računalnikom in na različnih mestih merili v odvisnosti od časa, bi dobili podatke, ki bi jih lažje primerjali s simulacijo, prav tako pa bi se znebili negotovosti, ki je izvirala iz dinamične narave našega projekta, ker se hitrost nepredvidljivo spreminja v odvisnosti od časa. Lahko pa bi opravljali poskus pri večjih hitrostih, ker bi tako relativna napaka meritev bila manjša.
Pod naključne napake pa bi lahko uvrstili temperaturo prostora v katerem smo delali. Poskuse smo izvajali v razponu štirih tednov in pred in po sončnemu zahodu, kjer so bile temperature različne, kar je zagotovo prispevalo k dinamiki tokov in izmerjenim hitrostim vetra. Pri prvem in tretjem poskusu, pa ima temperatura vpliv tudi na ugašanje sveče, ker pri ohlajujočem vremenu nastaja vedno večja temperaturna razlika med zrakom in plamenom zaradi katerega plamen izgublja več toplote, kar pa pomeni, da jo veter »lažje« in prej ugasne. To negotovost bi težko nevtralizirali, saj je v šolskem prostoru skoraj nemogoče vzdrževati konstantno temperaturo, lahko pa bi ob izvajanju poskusa zraven tudi merili temperaturo in bi tako imeli boljši pregled o vplivu temperature na naše meritve.
Kot pa smo že omenili, bi h kakovostnejšim podatkom, ki bi jih lahko primerjali s simulacijo ali pa za boljši »fit« grafov zagotovo doprineslo večje število meritev.
Theory
Combustion theory can suggest a reason why we might have noticed the variation in the velocity at which the candle is extinguished.
Candle Working Principle
Candles are typically made of petroleum-derived paraffin wax with 20-30 carbon atoms and use a wick made of cotton to transport the wax by capillary action to the flame zone.[1],[2] The wax is not ignitable as a liquid and solid, as shown in video 1. However, Faraday's well-known lectures on candles[3] suggest that wax vapor is ignitable and is thus the fuel for the combustion reaction in the candle. In this demonstration, the candle reaches steady-state combustion and is then quenched. The vapor, which emanates from the top of the wick, can then be lit so the flame travels along the gas down to the wick tip, where it reignites the candle. This demonstration is reproduced in video 2 and also suggests that the liquid wax pooled at the bottom of the wick is transported by capillary action to the top, where the vapor origin appears.Video 1: No ignititon of solid and liquid waxVideo 2: Reignition of candle using gaseous wax
Laminar Diffusion Flames
The features of a candle flame and its extinction are described by diffusion combustion. The candle wax vapor and the oxygen react at their interface, where the reaction is limited by the rate of diffusion of these mixtures or their chemical reaction rate.[4] The Damköhler number is crucial to studying these flames because it encodes whether the dominant factor in the combustion is the flow rate or the chemical reaction rate. When the Damköhler number is large, the flame surface can consume as much fuel and oxidizer as it is provided. However, at a smaller Damköhler number, the heat of the flame is convected away, reducing the reaction rate. Fendell[5] found a relation between the Damköhler number and the maximum temperature achieved by the flame under some conditions.[6] This phase plot is reproduced below. Qualitative steady state phase plot reproduced from Fendell showing the turning point where the system state jumps down to the frozen branch, and where the unstable region is denoted with a dotted line
Qualitative steady state phase plot reproduced from Fendell showing the turning point where the system state jumps down to the frozen branch, and where the unstable region is denoted with a dotted line
The image shows an upper branch, a lower branch and an unstable region in between. As the Damköhler number decreases from , so does the temperature, causing not all the reactants to burn. The phase plot shows this as a system traveling along the upper branch towards the right. If the Damköhler number decreases enough, the resulting lower temperature is fed back into the reaction rate, which will also be lower until the flame is unable to sustain itself and the flame is quenched. The turning point in the phase plot where the upper branch approaches the unstable region and then jumps down to the lower branch where the temperature is too low to produce a flame, encodes this phenomenon. The Damköhler number at this turning point is the extinction parameter that we can use to think about what conditions cause the different extinction velocities we observed experimentally.
Turbulent Diffusion Mixing
The flow pattern formed by a system is crucial to estimating the amount of flow that is used in the Damköhler number. Adding a cylinder to the system perturbs the flow, resulting in different flow patterns that depend on the Reynolds number . This number represents the ratio between the convective inertial term, , and the dissipative term, , in the Navier-Stokes equation.[7] When the dissipative term is large, the system tends to be steady with minimal mixing and eddies because perturbations are quickly smeared into molecular motion due to the dominating viscosity; however, at high Reynolds numbers, the perturbations can develop into large, almost chaotic velocity gradients that can create more mixing. To demonstrate the difference in flow at different Reynolds numbers, we wrote a fully coupled P2-P1 finite element solver with an implicit backward difference second-order time scheme[8] for incompressible Navier-Stokes whose code is available here. The images below show a relatively low Reynolds number flow around a cylindrical obstacle, which is the steady state that is eventually reached. The videos, however, show the effect of a higher Reynolds number flow that never becomes steady and contains mixing eddies. This Reynolds number is still not high enough to show any chaotic behavior or the true behavior in our experiment which, given the nonlinearity of the Navier-Stokes equations, could also look qualitatively different than this simulation. This is difficult to compute on a consumer device because the grid steps time steps required to simulate this scale as . This does, however, give us a feel for the behavior as the Reynolds number increases. As discussed before, it is reasonable to expect even greater vorticity and mixing in our experiment due to its higher Reynolds number.
In our experiment without the cylinder, the velocity at which the candle was extinguished was higher than the velocities measured in the experiment with the cylinder, where the flow was perturbed. The onset of turbulence in the perturbed flow could explain the different extinction velocities. Turbulent eddies that form in the flow field increase the rate of mixing of the reactants which, at high enough rates begins to dominate over the finite rate chemical reactions. This in turn decreases the Damköhler number and can thus cause flame extinction due to excessive rates of diffusive heat loss.[9] While the convective flow required to blow out the candle in the more turbulent experiment was lower, the increase in the diffusive flow rate due to the turbulence still allowed the overall flow rate to increase enough to reach the extinction Damköhler number.
However, due to discrepancies between our heatmap velocities and the extinguishing velocities in the same positions, as well as our limited ability to isolate the direction of flow, we were not able to draw any meaningful conclusions about why the extinguishing velocity was changing behind the cylinder. This may be due to turbulent eddies but we are unable to confirm their magnitude and thus how the extinguishing velocity might be related.
Images of steady flow at equilibrium and Videos 3: Unsteady flow at References
[1] Hamins, A. (2005). Characterization of candle flames. Journal of Fire Protection Engineering, 15(4), 265-285. https://doi.org/10.1177/1042391505053163
[2] Takahashi, F. (2009). Candle and Jet Diffusion Flames: Mechanisms of Combustion under Gravity and Microgravity Conditions. In Combustion Phenomena: Selected Mechanisms of Flame Formation, Propagation, and Extinction (pp. 170-178). essay, CRC Press.
[3] Faraday, M., Biederstedt, R. F., & Davenport, D. A. (1992). A transcription of Michael Faraday's lecture notes for his course of six elementary lectures on chemistry adapted to a juvenile audience: Presented at the Royal Institution of Great Britain, during the Christmas season of 1827. Princeton, NJ: Woodrow Wilson National Fellowship Foundation.
[4] Williams, F. A. (1985). Combustion Theory: The Fundametal Theory of Chemically Reacting Flow Systems. Addison-Wesley.
[5] Fendell, F. E. (1965). Ignition and extinction in combustion of initially unmixed reactants. Journal of Fluid Mechanics, 21(02), 281. https://doi.org/10.1017/s0022112065000186
[6] Law, C. K. (2006). Combustion Physics. Cambridge University Press.
[7] Reddy, J. N., & Gartling, D. K. (2010). The Finite Element Method in Heat Transfer and Fluid Dynamics. Boca Raton, FL: CRC Press.
[8] Quarteroni, A. (2014). Numerical Models for Differential Problems. Milan u.a.: Springer.
[9] Lignell, D. O., Chen, J. H., & Schmutz, H. A. (2011). Effects of Damköhler Number on Flame Extinction and Reignition in Turbulent Non-Premixed Flames using DNS. Combustion and Flame, 158(5), 949-963. https://doi.org/10.1016/j.combustflame.2010.10.027