Uvod

Če vzamemo dve vrvi in dva konca na isti strani fiksiramo, potem pa na druga dva konca obesimo utež in ju začnemo vrteti okrog osi, ki je vzporedna z vrvema, potem opazimo, da če konec izpustimo, se vrvi vrneta nazaj v prvotno lego in okrog nje nihata (to vidimo v videu 1). Namen te naloge je določiti lastnosti tovrstne "vrvne vzmeti". V okviru te naloge smo se odločili, da bomo poiskali, kako je navor te vzmeti odvisen od lastnosti vrvne vzmeti (njenega preseka, vrste materijala, s kolikšno silo je napeta in gostote navojev na dolžinsko enoto pri začetku meriritve), saj ga je lahko izmeriti in nato primerjati kako se spreminja z lastnostmi vzmeti. Ker za navadno torzisko vzmet velja sledeča enačba: $$M = D \theta$$ pri čemer je \(D\) torzijski koeficient in \(\theta\) kot zasuka izven ravnovesne lege. Nas zanima kakšna je odvisnost navora M od kota zasuka \(\theta\), zato bomo poizkusili najti funkcijo, da bo veljalo: $$ M = f(\theta)$$ pri čemer je \(\theta\) kot zasuka izven ravnovesne lege. Koeficienti v tej funkciji bodo odvisni od lastnosti vzmeti, saj če zamenjamo vrv, bomo pri istem zasuku izven ravnovesne lege dobili drugačen navor. Zato bomo raje kot navor primerjali koeficiente dobljene funkcije in kako se ti z spremembo lastnosti vzmeti spreminjajo. Tako bomo lahko na dober način opisali lastnosti vrvne vzmeti. Navor pa lahko zapišemo tudi kot: $$M = J \alpha$$ Pri čemer je \(J\) vztrajnostni moment telesa, \(\alpha\) kotni pospešek telesa, \(M\) zunanji navor. Sedaj pa lahko napišemo enačbo: $$f(\theta) = J \alpha(\theta) $$ \(\alpha\) se da izmeriti z optičnimi vrati, \(J\) pa lahko izračunamo, tako da premerimo in stehtamo utež. Z prirejanjem funkcij na izmerjene podatke in primerjanjem le teh, bomo lahko določili odvisnosti koeficientov od lastnosti vzmeti.

Zasnova eksperimenta

Za izvedbo projekta smo uporabili naslednje pripomočke:

1. tehnica,

2. dve stojali,

3. prižemo z okroglo luknjo,

4. rdečo pleteno vrv,

5. tanko belo elastično vrv,

6. debelo belo elastično vrv,

7. debelo belo pleteno vrv,

8. optična vrata,

9. ošpičeno palico,

10. lab pro vmesnik,

11. računalnik

slika 1: tehnica	slika 2: lab pro vmesnik	slika 3: računalnik

Na statično železno palico smo pritrdili prižemo, na katero smo pritrdili vrv in z vrvjo naredili zaključeno zanko (2 vzporedni vrvi). Vozel te zanke smo namestili na prižemo, da ne bi motil meritve. Na konec vrvi smo obesili utež, na katero smo nalepili 8 tankih lahkih lesenih palčk v radialni smeri glede na utež (slika 5). Namen le teh je bil prekinitev svetlobnega žarka v optičnih vratih, ki so nemenjena temu, da merijo število vrtljajev v odvisnosti od časa (sliko 5). Vsaka taka prekinitev je predstavljala absoluten zasuk uteži in vrvi za \(45^{\circ}\), vendar optična vrata ne morejo določiti smeri vrtenja. Tako imamo efektivno 2 vrvi, ki se spiralno prepletata in lahko merimo, za koliko se zavrtita iz ravnovesne lege in časovno odvisnost teh odmikov. Pri tem smo predpostavili:

1. da je naša utež narejena iz valjastih vzmeti (dejansko imajo malo zarezo in niso popolnoma valjaste),

2. vrvi so neraztegljive,

3. palčke, ki smo jih nalepili so lahke in ne prispevajo k vztrajnostnemu momentu,

4. dve sosednji palčki sta pod kotom \(45^{\circ}\) (njihova debelina je 0),

5. os vrtenja je pri miru (naša se je minimalno vrtela),

6. os, na kateri so uteži, ne prispeva vztrajnostnega momenta,

7. koeficienti funkcije \(f\left(\theta \right)\) so za pol nihaja konstantni,

8. frekvenca nihanja se med polovico nihaja ne spreminja.

slika 4: eksperiment	slika 5: optična vrata in utež

slika 6: nastavek z luknjo za vrvi	video 1: video poskusa	slika 7: vrvi

Podatke o stanju optičnih vrat smo zbirali s programom logger pro ter jih nato obdelali v pythonu. V okviru eksperimenta smo testirali 4 različne vrvi; dve od teh sta bili iz elastičnega materijala (te smo deformirali do točke, kjer se vrv ni več raztegovala), preostale vrvi so bile iz neraztegljivega materijala. Vrvi smo oštevilčili z 1 (rdeča pletena vrv)(te nismo uporabili, saj je po parih meritvah imela ravnovesno lego pri nekje okoli 30 navojih), 2 (tanka elastična bela vrv), 3 (debela elastična bela vrv) in 4 (pletena bela debela vrv). V enakem vrstem redu so razvrščene od vrha navzdol na sliki 7. Kotni pospešek obešene uteži smo merili pri različnih parametrih (različni dolžini vzmeti, različnem številu navojev na začetku meritve, različnem preseku vrvi in različni obešeni masi (napetosti vzmeti) ter različnih vrveh).

Teoretično ozadje

Torzijsko nihanje je vrsta nihanja, pri katerem se objekt vrti okoli svoje osi in pri čemer se kot vrtenja \(\theta\) s časom \(t\) spreminja. Lahko si ga predstavljamo kot rotacijski ekvivalent linearnega nihanja (npr. uteži na vzmet). Namesto premikanja gor in dol se objekt vrti levo in desno. Opis s diferencialno enačbo. Rotacijsko gibanje okoli osi opisujemo z kotom vrtenja \(\theta\) in kotnim pospeškom \(\alpha\). Kotni pospešek je drugi odvod kota vrtenja po času:

$$\alpha = \frac{d^2 \theta}{dt^2}$$

Vztrajnostni moment \(J\) telesa predstavlja vztrajnost telesa pri spremembi vrtilnega stanja. Za vsako telo ga lahko izračunamo po sledeči enačbi: $$ J = \int{r^2dm} $$ Pri čemer je \(dm\) košček mase telesa, \(r\) pa razdalija med koščkom mase \(dm\) in osjo vrtenja. Torzija je vrsta deformacije, ki jo povzroča sukanje okoli osi. Torzijski koeficient \(D\) vzmeti opisuje njeno odpornost proti zasuku izven ravnovesne lege. Če ni zunanjih navorov, je navor okoli osi vrtenja enak navoru zaradi torzije vzmeti. Matematično lahko to izrazimo z enačbo:

$$J \alpha = -D \theta$$

Negativnen znak na desni strani pomeni, da je navor vzmeti nasproten smeri vrtenja (za nas bo pomembna samo velikost navora, zato bomo minus izpustili).

Rešitev enačbe in pomembni parametri

$$\theta \left(t\right) = A \sin(\omega t + \phi)$$

Pri čemu so:

• \(A\) amplituda nihanja (maksimalni kot odklona),

• \(\omega\) kotna hitrost nihanja (frekvenca v radianih na sekundo), ki jo določimo s:

$$\omega = \sqrt{\frac{D}{J}}$$,

• \(\phi\) faza nihanja (odklon od ravnovesnega stanja pri začetnem času).

Obdobje nihanja \(T\) je čas, ki ga potrebuje objekt, da se iz danega položaja vrne v isti položaj, in se izračuna kot:

$$T = \frac{2\pi}{\omega}$$

Frekvenca nihanja \(\nu\) predstavlja število nihajev na enoto časa in jo izračunamo kot:

$$\nu = \frac{\omega}{2\pi}$$

Navor torzijskega nihala

Velikost navora je odvisna od kota zasuka nihajnega telesa (θ) in torzijskega koeficienta vzmeti (D) in jo opisuje naslednja enačba:

$$M = D \theta$$

Vztrajnostni moment valja okoli njegove osi vrtenja je odvisen od mase \(m\) valja in njegovega polmera \(r\). Ker so bile naše uteži valjaste, je to edina formula, ki smo jo potrebovali. Izračuna se s spodnjo formulo:

$$J = \frac{1}{2} m r^2$$

Dušenje nihanja

V resničnem svetu torzijska nihanja niso popolna in energija nihanja se sčasoma izgubi zaradi trenja ali drugih dejavnikov. To upoštevamo z uvedbo dušilnega člena v enačbo gibanja. S tem dobimo bolj splošno obliko enačbe:

$$J \alpha + b \omega + D \theta = 0$$

Pri čemer je b koeficient dušenja, ki je sorazmeren hitrosti izgubljanja energije. Višja kot je vrednost koeficienta dušenja, hitreje nihanje pojenja. V primeru majhnega dušenja lahko enačbo poenostavimo in ohranimo prej predstavljeno rešitev.

Analiza podatkov

Grafe smo narisali v pythonu. Ker je vztrajnostni moment aditivna količina smo najprej izračunali vztrajnostini moment posameznim valjastih uteži in jih potem sešteli. Enačba za vztrajnostni moment enega valja je:

$$J = \frac{1}{2} m r^2$$

$$J_{n} = \frac{1}{2} m_{n} + 2r_{n}$$

Pri čimer je \(m_{n}\) relativna negotovost izmerjene mase in \(r_{n}\) relativna negotovost izmerjenega r

Nato smo sešteli vse te vztrajnostne momente in dobili, da je vztrajnostni moment celotne uteži:

$$J = \sum{J_i}$$

$$J_{an} = \sum{J_{ani}}$$

$$J_{n} = \frac{J_{an}}{J}$$

Pri čimer je \(J_{an}\) absolutna negotovost količine, \(J_{n}\) relativna negotovost količine. Vztrajnostni moment celotne uteži je:

$$J_1 = 2,76 \times 10^{-4} (1 \pm 0,033) kg/m^2$$

Vztrajnostni moment brez dveh 50 gramskih uteži:

$$J_2 = 2,15 \times 10^{-4} (1 \pm 0,034) kg/m²$$

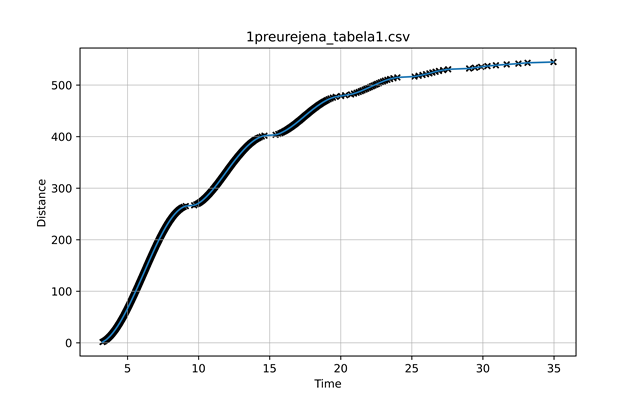
Sledeči grafi prikazujejo kot, kotno hitrost in kotni pospešek v odvisnosti od časa. Ker z našo opremo nismo mogli ločiti, ali se vrti naša utež v desno ali v levo, smo lahko le seštevali absolutne vrednosti zasukov. Za vsako prekinitev v optičnih vratih smo prišteli \(45^{\circ}\) celotnemu zasuku, kot je prikazano na grafu.

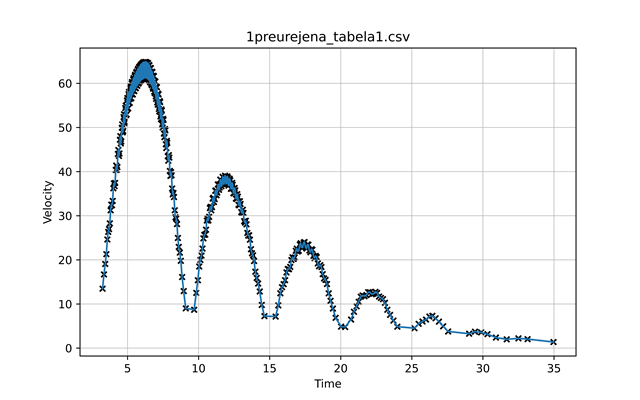
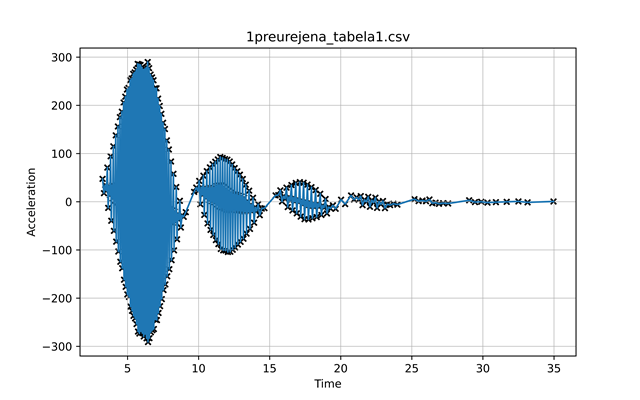
graf 1: kot v odvisnosti od časa	graf 2: kotna hitrost v odvisnosti od časa	graf 3: pospešek v odvisnosti od časa

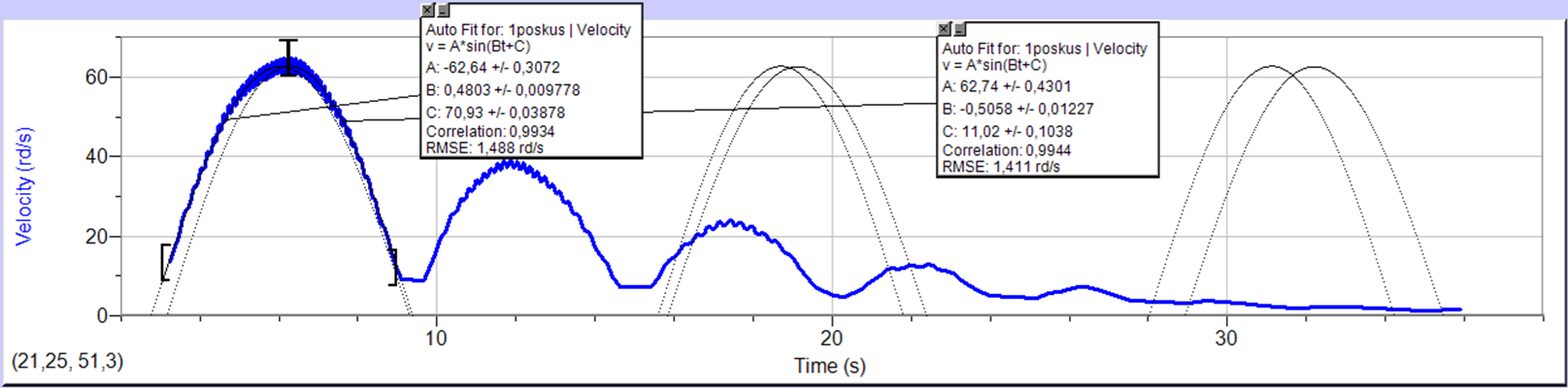
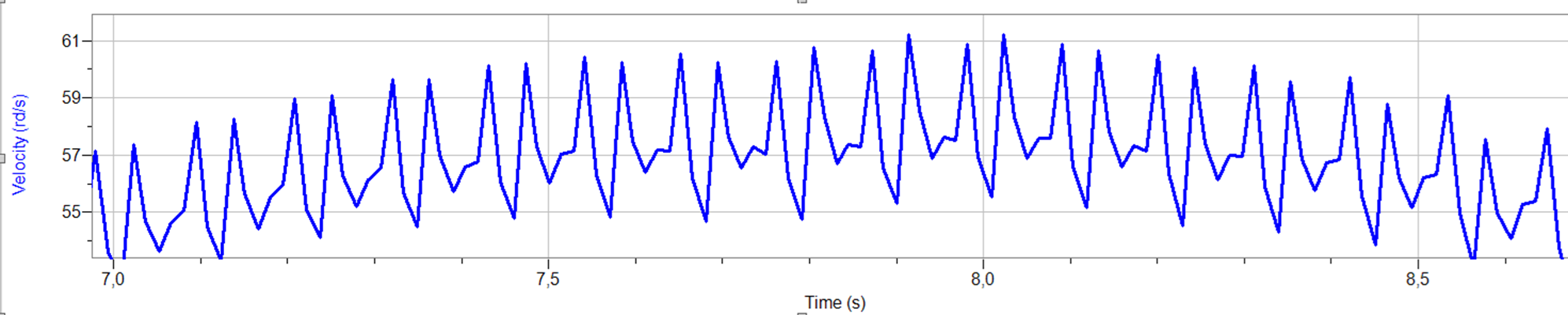
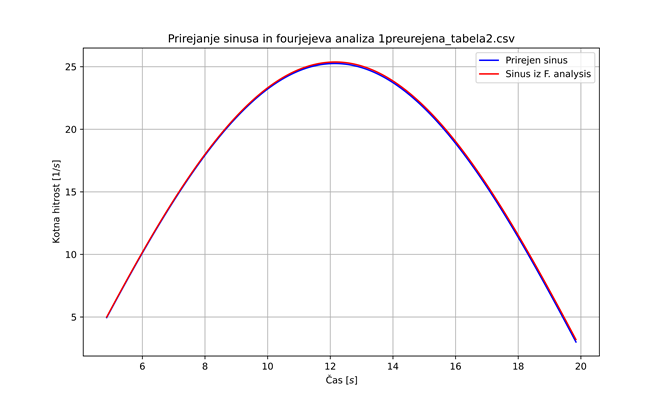
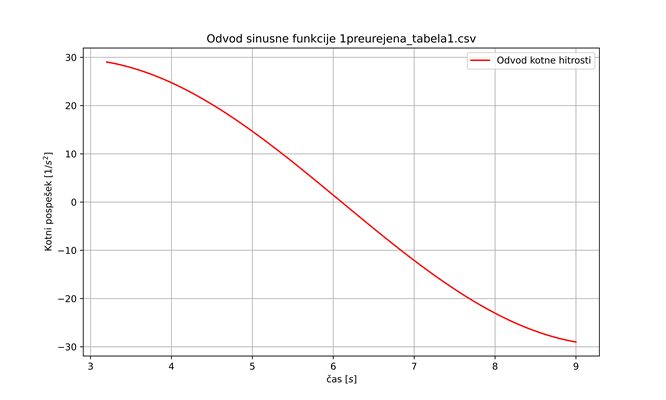
Iz grafa 2 je razvidno tudi, da je nihanje uteži na naši vrvni vzmeti dušeno, ampak to nas pri določanju torzijskega koeficienta ne zanima. Ker razmiki med robovi palčk niso bili enaki, smo dobili nažagan graf kotne hitrosti (primer graf 2 in graf 5); enkrat je razdalja med palčkama manjša od \(45^{\circ}\) in je zato čas med tem, ko vsaka prekine manjši, kot bi bil, če bi bili točno \(45^{\circ}\) narazen, tako vzamemo manjši čas, kot ga utež v resnici rabi za zasuk \(45^{\circ}\). Zato dobimo večjo kotno hitrost na tem intervalu. V nasprotnem primeru, če sta palčki več kot \(45^{\circ}\) narazen, dobimo obraten efekt. Kotna hitrost na intervalu je manj kot je v resnici. Ker nobena roba palčk nista za \(45^{\circ}\) narazen, kot smo predpostavili, imamo na vsaki meritvi enega od teh dveh efektov. Posledica je nazobčen graf kotne hitrosti ter nerealen graf kotnega pospeška (primer graf 3). Da bi se prepričali, če je to res vzrok, bi lahko na utež dali eno samo palčko in točno določili kot med njenima krajiščema. Prav tako se iz grafa 4 vidi, da je frekvenca grafa sinusa prirejenega na del grafa, ki predstavlja navijanje in na del grafa, ki predstavlja odvijanje različna. To je verjetno posledica tega, da vrv zdrsi pri odvijanju, saj sila lepenja med navoji ni dovolj velika, posledično se zato vrv odvrti hitreje. To bi lahko preverili tako, da bi vrv namočili v olje in s tem zmanjšali koeficient trenja. Če je naša hipoteza pravilna, bi bila pri vrvi, namočeni v olje, razlika še večja. Mi smo predpostavili, da je v prvem približku enaka (iz grafa 4 se vidi, da je negotovost majhna in jo lahko zanemarimo). Da bi se znebili šuma, smo naredili fourierjevo analizo (primer graf 6). Izločili smo frekvence, ki so glede na frekvenco nihanja uteži, te smo ocenili iz grafov kotnih hitrosti (primer graf 2), zelo visoke. Temu grafu smo priredili sinusno funkcijo \(a\sin(\omega t + \varphi)\) (primer graf 6). Tako prirejena sinusna funkcija se je skoraj popolnoma prilegala grafu po fourierjevi analizi. Prirejeno sinusno funkcijo smo odvajali in dobili graf kotnega pospeška (primer graf 7). Ker ima vsak pol nihaj (na grafu en hrib) drugačno frekvenco, smo to naredili za vsak pol nihaj posebaj (razvidno iz grafa 2 in 4).

graf 4: prirejen graf sinusa za navijanje in odvijanje	graf 5: primer "nažagane sinus krivulje"

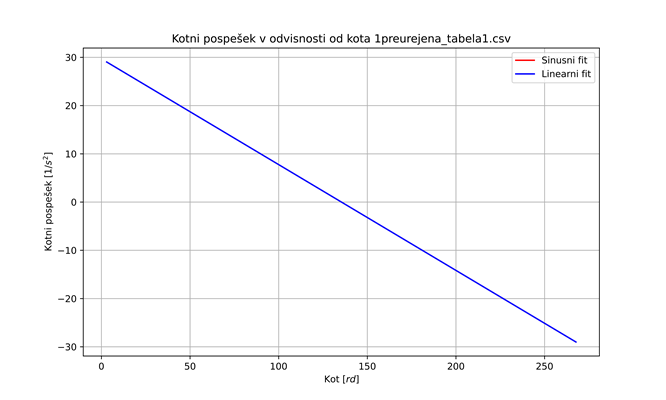
graf 6: kotna hitrost po fourierjevi analizi in nanjo prirejena sinusna funkcija	graf 7: odvod prirejene sinusne funkcije	graf 8: kotni pospešek v odvisnosti od kota zasuka (prirejena linearna funkcija)

Enako smo naredili za vse grafe. Iz vsakega grafa pospeškov smo vzeli kotni pospešek pri vsakem izmerjenem kotu, se pravi dva kotna pospeška sta izmerjena pri zasukih, ki se razlikujeta za π/8. Nato smo naredili grafe kotnega pospeška v odvisnosti od kota zasuka (primer graf 8). Na njega smo priredili več različnih funkcij in se je izkazalo, da se najbolje prilega linearna funkcija (graf 8). Za tak pristop smo se odločili, ker je bilo iz grafa kotne hitrosti lažje določiti začetek in konec polovice nihaja, kot pa iz grafa kota. Ker je kotni pospešek v odvisnosti od kota linearna funkcija, velja naslednja zveza:

$$\alpha =k\theta$$

$$ M = f(\theta) = J \alpha(\theta)$$

Če je kotni pospešek linearna funkcija, bo potem tudi navor, saj, da ga izračunamo le pomnožimo kotni pospešek z vztrajnostnim momentom.

$$M = D\theta$$

$$J\alpha = D\theta$$

$$\alpha = \frac{D}{J} \theta$$

Pri čemer je k koeficient prirejene premice, \(J\) vztrajnostni moment uteži in \(D\) torzijski koeficient.

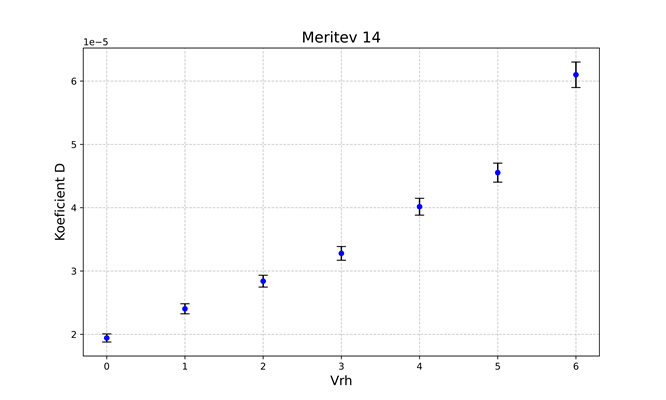
Ko smo zgornjo enačbo uporabili za vsak hrib posebej smo dobili \(D\) za vsak posamičen hrib. Iz rezultatov je vidno, da ima vsak naslednji hrib večji \(D\) (graf 9).

slika 8: tabela podatkov

graf 9: primer grafa \(D\) v odvisnosti na kateri polperiodi je bil izmerjen

Pri meritvah največjo negotovost doprinese vztrajnostni moment. Ker smo merili z optičnimi vrati, imajo naše meritve časov zamemarljive inštrumentalne negotovosti. Nažaganost kotne hitrosti v našem primeru ni smiselno vzeti kot inštrumentalno negotovost, saj ko naredimo fourierjevo transformacijo in odstranimo zelo visoke frekvence, je dobljen graf skoraj sinusna funkcija (graf 6). Takšen graf ni več nažagan, zato ima zanemarljivo negotovost. Tega smo pa uporabljali pri računanju. V okviru te naloge smo naredili premalo meritev, da bi lahko izračunali slučajne negotovosti. Koeficient \(k\) je tudi imel zanemarljivo negotovost, saj se prirejena linearna funkcija skoraj popolnoma prilega na graf \(\alpha(\theta)\). Mi smo uporabili pravilo najšibkejšega člena, se pravi negotovost našega končnega rezultata je največja relativna negotovost količine v izračunu (to je bila relativna negotovost vztrajnostnega momenta).

Iz tabele se ne da veliko sklepati, saj imamo premalo meritev, če spremenimo le en parameter. Narediti bi jih morali več in potem bi lahko prirejali funkcije (na dve točki namreč lahko priredimo različne funkcije in dobimo popolno prilegnje) $$ D = f(p)$$ pri čimer je p poljubna lastnost vrvne vzmeti. Vseeno smo lahko ugotovili naslednje:

1. iz \(D\)-jev različnih hribov je razvidno, da je pri vsakem naslednjem hribu navor pri istem kotu zasuka izven ravnovesne lege večji, primer graf 9. To je posledica raznih notranjih torzij vrvi (vrv se ne obnaša kot žica, ta se po torziji, če ni presežena meja prožnosti vrne v ravnovesno stanje, pri vrvi se pa med torzijo nekaj zgodi, ki poveča \(D\)).

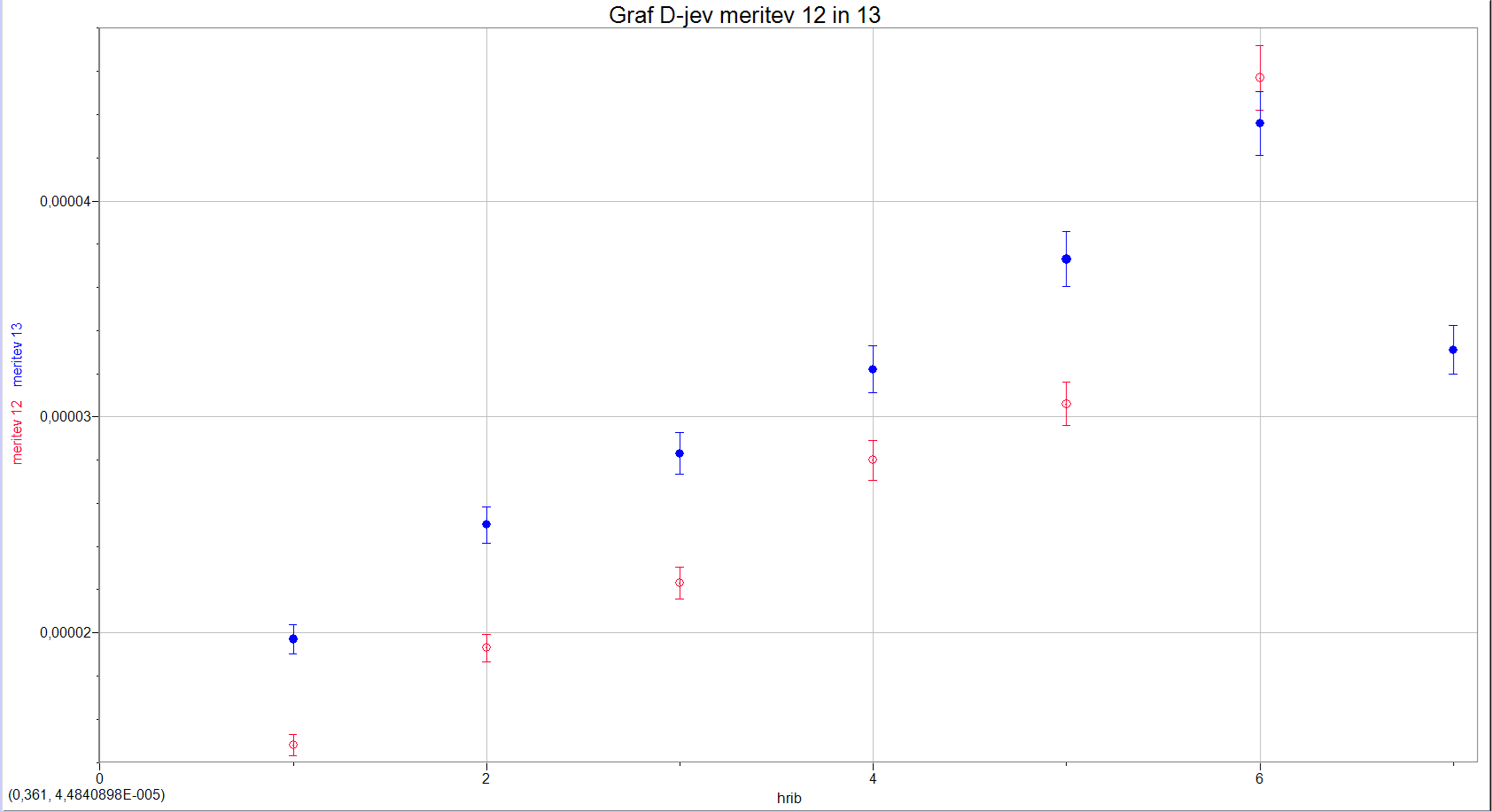
2. napetost vrvne vzmeti vpliva na \(D\). To vidimo, če v tabeli pogledamo dvanajsto in trinajsto meritev (graf 13), kjer spremenimo samo maso uteži in se koeficient \(D\) poveča kot posledica.

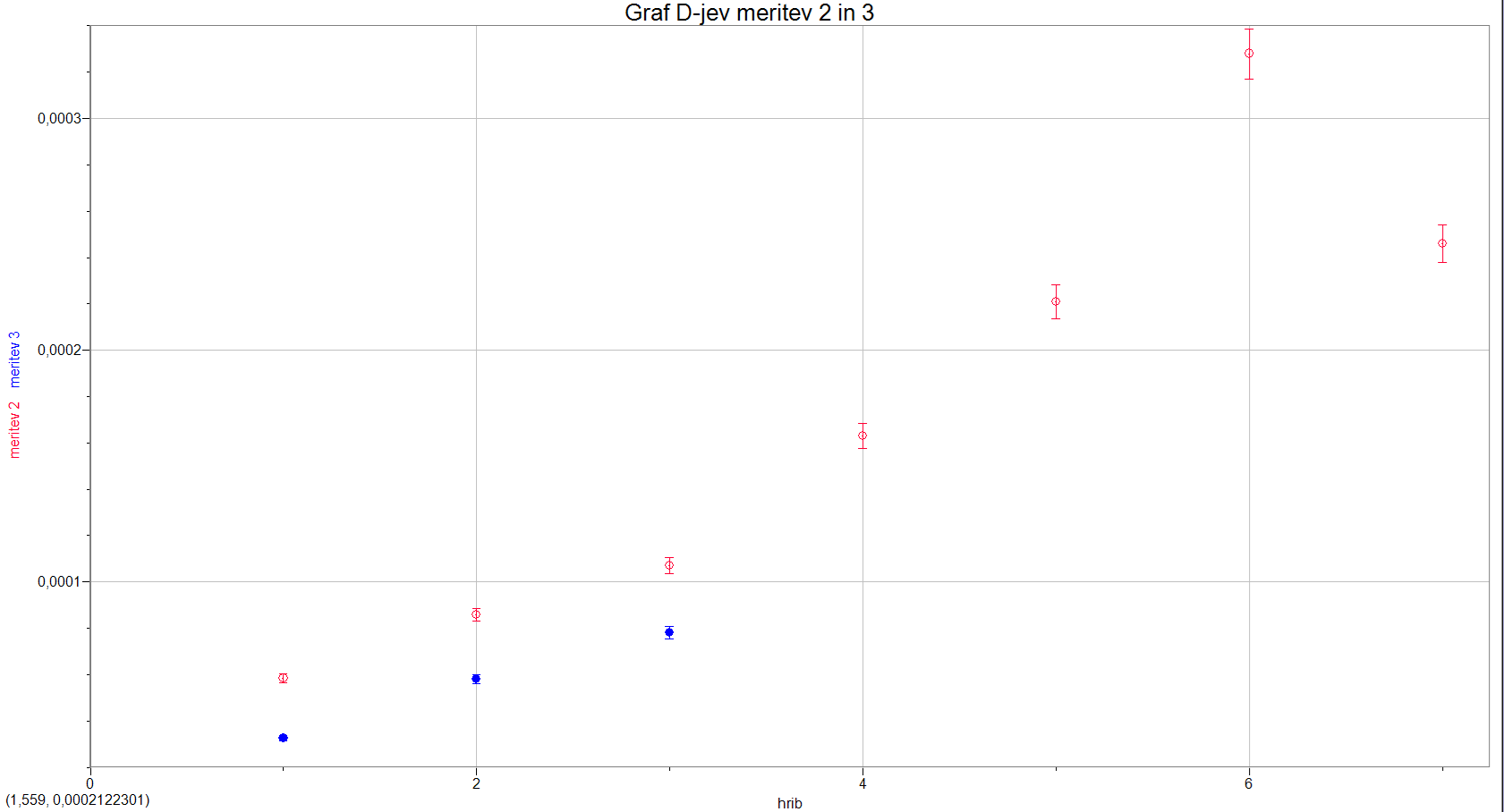
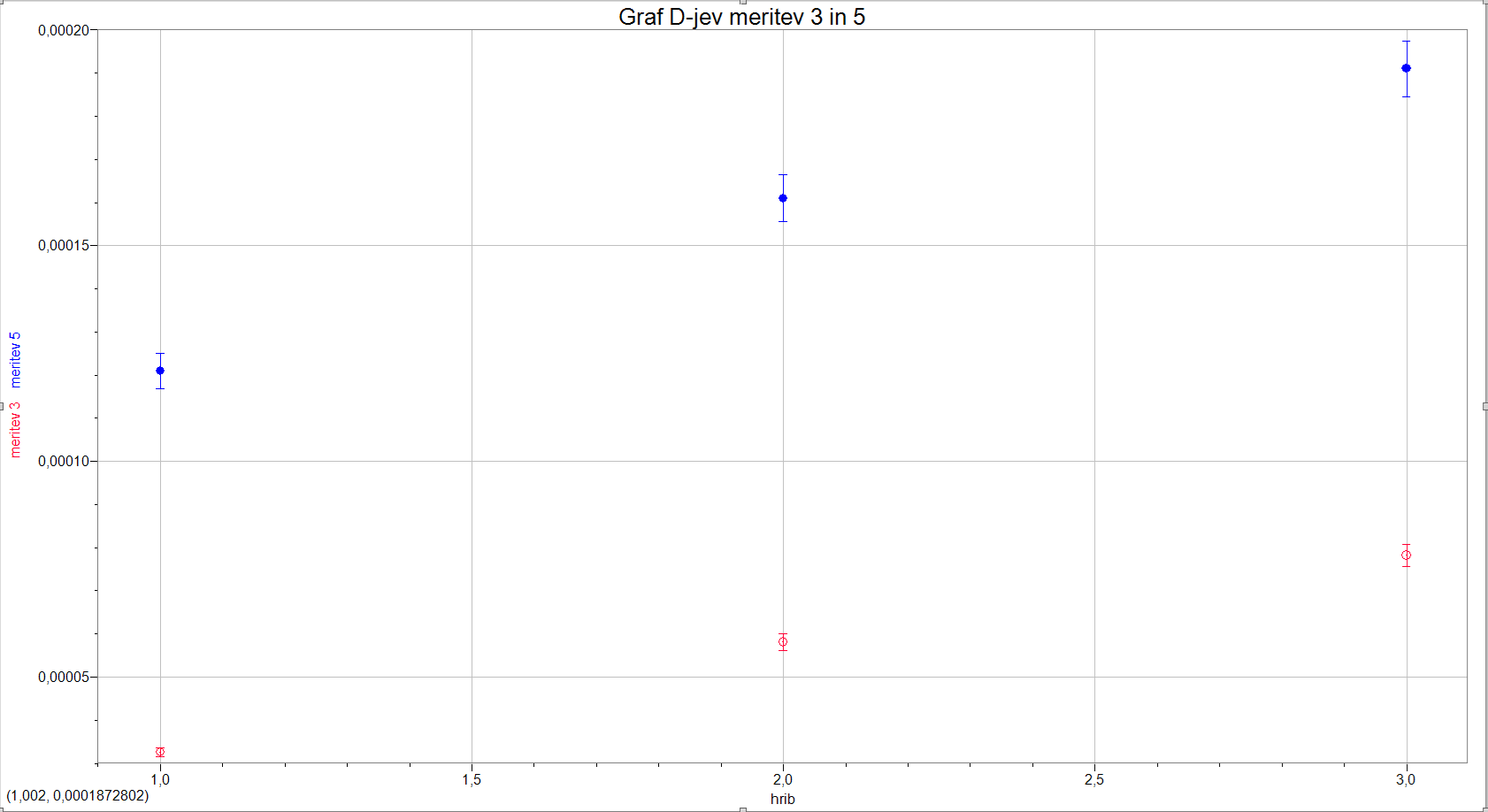
3. koeficient \(D\) ni odvisen od gostote navojev pri začetku meritve, ampak je odvisnost bolj temeljna, namreč je odvisen od dolžine vzmeti po neki funkciji in od števila navojev pri začetku meritve po drugi. To lahko vidimo, če pogledamo tretjo in peto meritev (graf 12) (gostota navojev se podvoji \(D\) naraste za štirikrat) ter drugo in tretjo meritev (graf 11) (tukaj se gostota navojev poveča za 2 krat in \(D\) se tudi poveča za 2 krat. Pri obeh meritvah spreminjamo le dolžino vzmeti in število navojev na začetku).

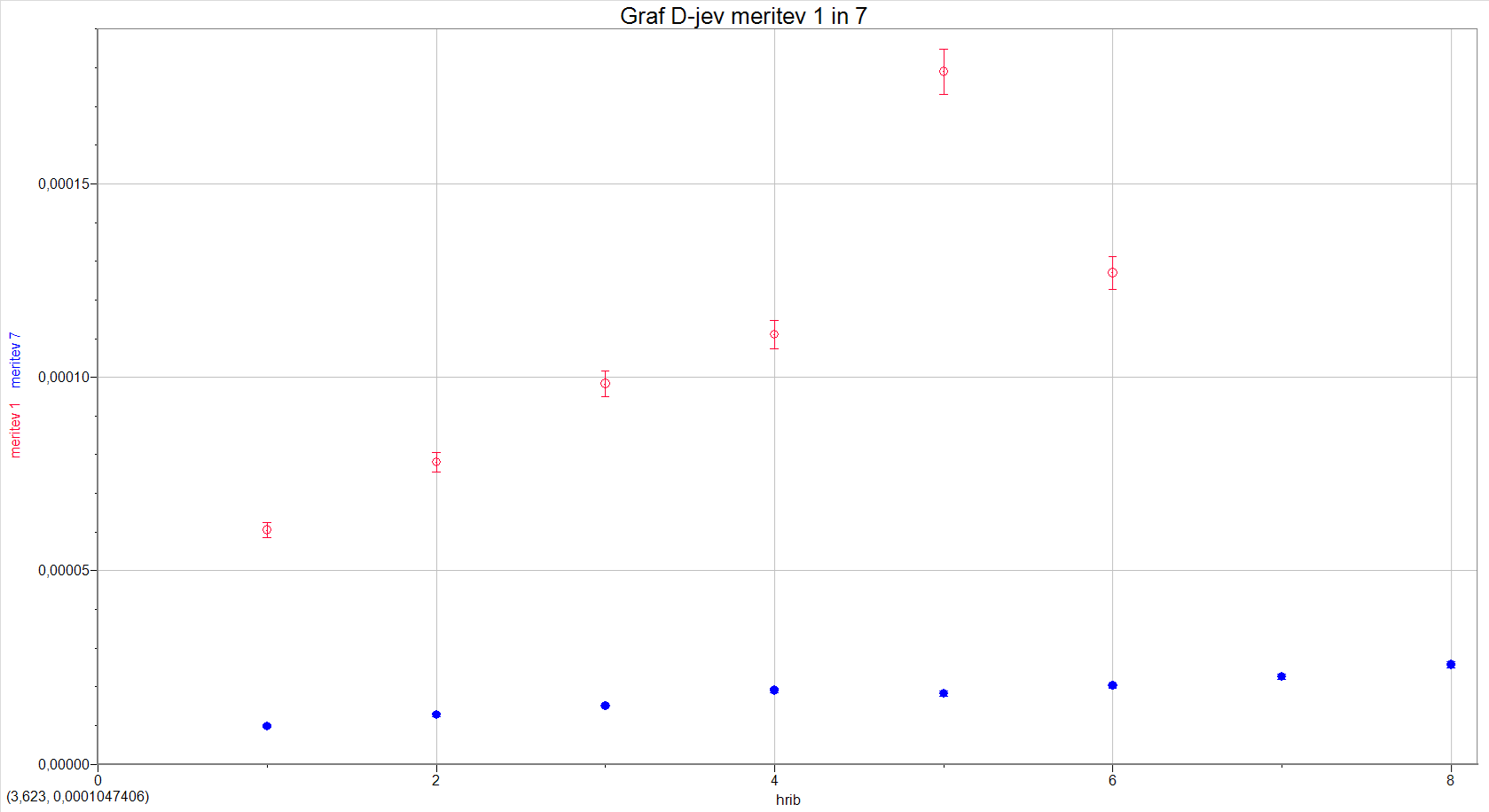
4. koeficient \(D\) je odvisen od preseka vrvi to je vidno iz prve in sedme meritve (graf 10) ti dve nista dovolj, da bi določili pravo odvisnost.

5. Za navijanje in odvijanje ne moremo prirediti istega sinusa, tako se prej odvije vzmet kot navije. To bi lahko pojasnili tako, da sila lepenja ni dovolj velika in vrv zdrsi in se tako prej odvije, saj se to ne more zgoditi, ko se navija.

graf 10: \(D\) 1. in 7. meritve v odvisnosti od števila hriba	graf 11: \(D\) 2. in 3. meritve v odvisnosti od števila hriba

graf 12: \(D\) 3. in 5. meritve v odvisnosti od števila hriba	graf 13: \(D\) 12. in 13. meritve v odvisnosti od števila hriba

Zaradi preglednosti vseh slik in grafov ni na spletni strani, te se lahko naloži preko spodnjih linkov:

ostale tabele in grafi

legenda csv tabel

V datoteki tabela z info.xlsx so zapisani kater csv tabela ustreza kateri realni meritvi.

Zaključek

Zaradi pomanjkanja meritev nam ni uspelo določiti odvisnosti \(D\)-ja od lastnosti vrvne vzmeti. Vselej nam je uspelo ugotoviti od česa je torzijski koeficient sploh odvisen. \(M\) je odvisen od napetosti vrvne vzmeti, njene dolžine, kota zasuka izven ravnovesne lege, preseka vrvne vzmeti, števila navojev pri začetku meritve ter tipa vrvi, iz katerega je narejena vrvna vzmet. Njegove odvisnosti od vrste materijala nam ni uspelo določiti, saj smo imeli premalo meritev. Naše meritve so dokaj natančne, D-je smo lahko določili na manj kot 4 procente natančno. Parametre smo določili tudi z veliko natančnostjo, razen preseka, saj je tega bilo težko natančno izmeriti, ker je bila vrv stisljiva ter zelo tanka.

Izboljšave

Meritve

Za boljši rezultat bi lahko na utež nalepili dolge igle oz. tanke lahke kovinske palčke. Problem smo imeli tudi z nihanjem uteži, v ta namen, bi utež enako obesili, ampak bi spodaj dodali še en ležaj, ki bi onemogočil, da bi utež prosto nihala. To isto težavo bi lahko popravili, če bi imeli dvojna optična vrata in bi jemali povprečne vrednosti časov za isti odmik. V okviru tega projekta nismo uporabljali vrvi debelejših od 2 cm, saj bi za vrvi debelejše od 5 cm potrebovali že nekaj deset kilogramske uteži in zelo dolge vrvi (tako bi dobili potrebne meritve za določitev \(D(S)\)). Problem smo imeli tudi z vrtenjem osi, na katero smo dajali uteži in neenakomernimi utežmi, kar je našim meritvam dalo večjo negotovost. Narediti bi morali več meritev, da bi imeli dovolj točk za prirejanje grafov \(D(p)\). Prav tako bi morali dati samo eno palčko na utež in izmeriti kot med njenima stranema. Tako se bi znebili periodično nažaganega sinusa.

Izbira vrvi

Med poskusom smo ugotovili, da vzmet deluje najbolje, če je narejena iz prožne in ne pletene vrvi. Tanka pletena vrv se nam je namreč ob obešanju uteži začela navijati (po nekajkratni uporabi je bila ravnovesna lega take vzmeti pri 30 navojih), poleg tega se je po več ponovitvah začela cufati.

Viri

slika v glavi: generated with the prompt “slika v stilu impresijonizma” by OpenAI, ChatGPT, 2024 (https://chat.openai.com/chat).

sliak za ozadje : generated with the prompt “slika v stilu impresijonizma” by OpenAI, ChatGPT, 2024 (https://chat.openai.com/chat).

Licenca