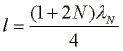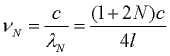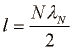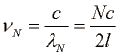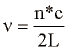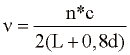ZVOČNO VALOVANJE:
Zvok je longitudinalno valovanje, ki se v splošnem širi v treh razsežnostih. Pri longitudinalnem valovanju delci nihajo vzdolž smeri širjenja in s tem nastajajo zgoščine in razredčine v zraku.
Spreminjanje tlaka pri valovanju:
Zvočne valove opišemo s premikom u vsakega majhnega delčka zraka, s tlakom (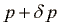 ) in z gostoto (
) in z gostoto (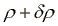 ). Z
). Z 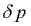 in
in 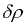 so označeni odmiki od pripadajoče ravnovesne vrednosti. Ker so amplitude zvočnih valov mnogo manjši od valovne dolžine, lahko
so označeni odmiki od pripadajoče ravnovesne vrednosti. Ker so amplitude zvočnih valov mnogo manjši od valovne dolžine, lahko 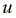 ,
, 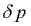 ,
, 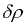 uporabimo kot diferenciale.
uporabimo kot diferenciale.
Diferencialna enačba ki povezuje te količine je: 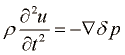
velja še kontinuetna enačba: 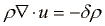
in enačba stanja v diferencialni obliki z adiabatično stislivostjo: 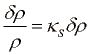
Iz teh treh enačb lahko izločimo 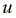 in
in 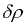 , da dobimo valovno enačbo za
, da dobimo valovno enačbo za 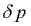 in hitrost zvoka:
in hitrost zvoka:
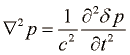
Bolj enostavno lahko napišemo odvisnost tlaka sinusnega valovanja, ki potuje v smeri osi x kot funkcijo kraja in časa:
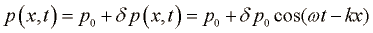
Kjer je p0 tlak v zraku ko ni valovanja. Amplituda nihanja tlaka 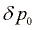 in amplituda odmika
in amplituda odmika 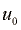 sta sorazmerni:
sta sorazmerni:
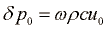
Hitrost zvoka v plinih je definirana kot:
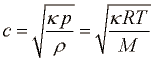
In je odvisna od vrste plina(M) in od temperature (T). Hitrost zvoka je istega velikostnega reda, kot povprečna hitrost molekul.
Valovanje v eni razsežnosti:
Valovna enačba zvoka za sinusno motnjo v eni dimenziji, v poljubni točki:
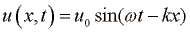
kjer je 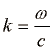 valovno število.
valovno število.
Odmik u, ki je funkcija kraja in časa, ima pri sinusnem valovanju dve periodi: krajevno in časovno. Na danem mestu odmik sinusno niha z nihajnim časom 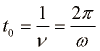 . Če gledamo trenutno sliko valovanja opazimo krajevno periodo ali valovno dolžino λ, pri čemer velja
. Če gledamo trenutno sliko valovanja opazimo krajevno periodo ali valovno dolžino λ, pri čemer velja 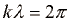 . Sinus je namreč periodična funkcija s periodo 2π. Upoštevajmo še zvezo
. Sinus je namreč periodična funkcija s periodo 2π. Upoštevajmo še zvezo 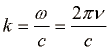 pa dobimo zvezo med frekvenco in valovno dolžino:
pa dobimo zvezo med frekvenco in valovno dolžino: 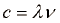 .
.
Stoječe valovanje:
Stoječe valovanje nastane, ko se srečata dve sinusni valovanji z enako frekvenco in amplitudo, ki potujeta v nasprotnih smereh:
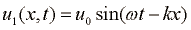
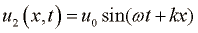
Na mestih kjer se valovanji srečata, je skupni odmik enak vsoti odmikov in tako dobimo stoječe valovanje:
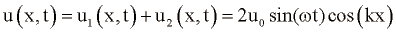
Pri stoječem valovanju imamo mesta, kjer je odmik u vseskozi enak nič 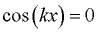 . Imenujemo jih vozli. Mesta, kjer je amplituda nihanja odmika največja
. Imenujemo jih vozli. Mesta, kjer je amplituda nihanja odmika največja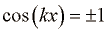 imenujemo hrbti. Razdalja med sosednjima vozloma je enaka razdalji med sosednjima hrbtoma stoječega valovanja. Enaka je
imenujemo hrbti. Razdalja med sosednjima vozloma je enaka razdalji med sosednjima hrbtoma stoječega valovanja. Enaka je 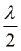
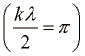
Stoječe valovanje srečamo pri strunah in piščalih.
Energijski tok:
Gostoto zvočnega energijskega toka j v akustiki imenujemo jakost zvoka. Pogosto jo izražamo v decibelih (dB) definiranih kot 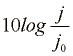 Tu je jakost zvoka j0 = 10-12 W/m2 približno enaka najmanjši jakosti zvoka, ki jo zazna uho pri frekvenci okrog 1kHz, ko je najbolj občutjivo. Nič decibelom ustreza jakost zvoka j = j0 = 10-12 W/m2, meji bolečine - 120 dB pa j = 1W/m2.
Tu je jakost zvoka j0 = 10-12 W/m2 približno enaka najmanjši jakosti zvoka, ki jo zazna uho pri frekvenci okrog 1kHz, ko je najbolj občutjivo. Nič decibelom ustreza jakost zvoka j = j0 = 10-12 W/m2, meji bolečine - 120 dB pa j = 1W/m2.
Gostoto zvočnega energijskega toka dobimo z enačbo: 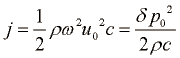
Če izmerimo amplitudo tlaka, lahko obrnemo enačbo in ven dobimo amplitudo odmika delcev: 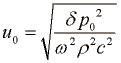 .
.
VALOVANJE V CEVI:
Obnašanje zvoka v cevi močno zavisi od dolžine cevi, njenega prečnega preseka, nepravilnostih na notranji strani cevi in robnih pogojev. V omejenem prostoru končnega volumna so možne proste oscilacije samo pri točno določenih frekvencah (lastnih frekvencah), načine nihanja pa imenujemo lastna nihanja.
Zaprta cev (na eni strani):
Dolžina cevi je enaka: 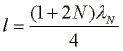
kjer so N števila (N = 0, 1, 2, ...)
To valovanje ima frekvence:
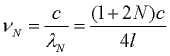
|
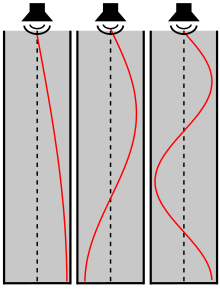
Prve tri resonance v zaprti cevi. Rdeča črta predstavlja amplitudo tlaka, tam kjer se rdeča črta dotika simetrale cevi (črtkana črta) je amplituda enaka nič. Tam kjer se dotika stene cevi, je pa maksimalna. (pri zvočniku je cev odprta) |
Odprta cev (na obeh straneh):
Dolžina cevi je enaka: 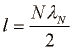
Kjer so N števila (N = 1, 2, 3, ...)
To valovanje ima frekvence:
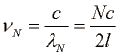 |
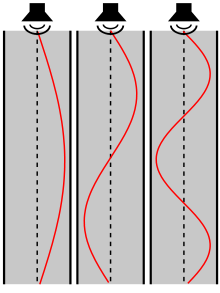
Prve tri resonance v odprti cevi. Rdeča črta predstavlja amplitudo tlaka, tam kjer se rdeča črta dotika simetrale cevi (črtkana črta) je amplituda enaka nič. Tam kjer se dotika stene cevi, je pa maksimalna. (pri zvočniku je cev odprta). |
POPRAVLJENE ENAČBE, KI UPOŠTEVAJO KONCE CEVI:
Odprte okrogle cevi:
Resonanco pri odprtih ceveh opazimo približno pri:
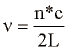
kjer je n naravno število, ki predstavlja število hribov in dolin valovanja, L dolžina cevi in c hitrost zvoka. Natančnejša enačba, ki upošteva popravke na obeh koncih cevi je:
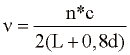
kjer d predstavlja premer cevi. Ta enačba upošteva dejstvo, da točka kjer se zvok odbije na odprtem koncu ni točno na koncu cevi, ampak malce izven cevi. Odbojnost je malo manj kot 1. Odprt konec se ne obnaša kot infinitezimalna akustična impedanca, ampak ima končno velikost, ki je odvisna od premera cevi, valovne dolžine in tipa odbojnih ploskev, ki so mogoče prisotne v bližini konca cevi.
Zaprte okrogle cevi
Zaprta cev bo imela resonance približno pri:
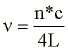
kjer n tokrat predstavlja liho pozitivno število (1,3,5...). Tak tip cevi ima torej osnovno lastno frekvenco za oktavo nižjo (polovica frekvence) kot odprta cev enakih lastnosti. Popravljena enačba ima obliko:
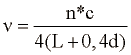
Znani enačbi za resonančne frekvence v cevi zadoščata za okvirno napoved frekvenc.
Natančnejše meritve pokažejo, da se pri določanju le teh za odprto cev splača uporabiti model podaljšane cevi po enačbi
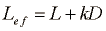
kjer je k približno 0,8. D je pa premer cevi.
Za zaprto cev pa nam zaradi majhnega števila meritev ni uspelo najti izboljšane enačbe, čeprav se je izkazalo, da osnovna ne zadošča.
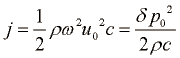
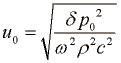 .
.

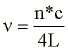
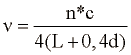
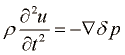
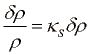
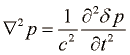
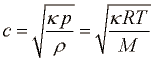
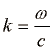 valovno število.
valovno število. 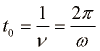 . Če gledamo trenutno sliko valovanja opazimo krajevno periodo ali valovno dolžino λ, pri čemer velja
. Če gledamo trenutno sliko valovanja opazimo krajevno periodo ali valovno dolžino λ, pri čemer velja 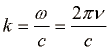 pa dobimo zvezo med frekvenco in valovno dolžino:
pa dobimo zvezo med frekvenco in valovno dolžino: 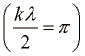
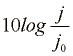 Tu je jakost zvoka j0 = 10-12 W/m2 približno enaka najmanjši jakosti zvoka, ki jo zazna uho pri frekvenci okrog 1kHz, ko je najbolj občutjivo. Nič decibelom ustreza jakost zvoka j = j0 = 10-12 W/m2, meji bolečine - 120 dB pa j = 1W/m2.
Tu je jakost zvoka j0 = 10-12 W/m2 približno enaka najmanjši jakosti zvoka, ki jo zazna uho pri frekvenci okrog 1kHz, ko je najbolj občutjivo. Nič decibelom ustreza jakost zvoka j = j0 = 10-12 W/m2, meji bolečine - 120 dB pa j = 1W/m2.