Meritve in izračuni
Krivinski radij
Prva od količin, ki smo jo izmerili je krivinski radij leče. Dobili smo naslednje rezultate:
| Leča | Radij |
|---|---|
| mala leča | 3,908 cm |
| velika leča | 7,155 cm |
| kondomska leča | 6,2 cm |
Lomni količnik
Ker smo delali z različnimi tekočinami smo morali preveriti lomni količnik za vse. Za zrak smo privzeli, da velja n(zraka)=1. Tako smo lahko merili količnik vode in olja. Zopet smo se poslužili analize fotografij. Na spodnjih dveh slikah vidimo pot laserskega žarka pri prehodu iz zraka v vodo oz. olje:
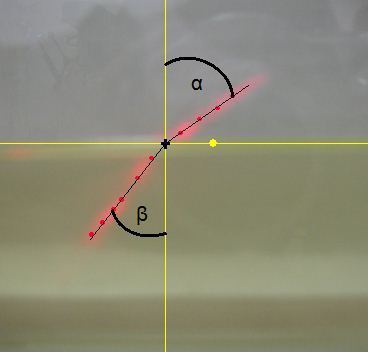
Obdelana fotografija loma na stiku zraka in olja
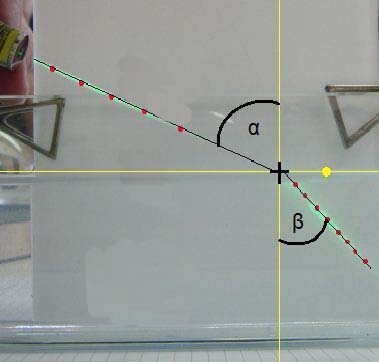
Obdelana fotografija loma na stiku zraka in vode
Naslednja slika pa prikazuje dejansko analizo v programu, ki nam pove, kakšen naklon imata žarka:
Končni izračuni pa so pokazali naslednje:
| Snov | Lomni količnik |
|---|---|
| voda | 1,31 |
| olje | 1,33 |
Rezultati so presenetljivo natančni glede na način merjenja.
Na kazalo
Goriščna razdalja
Najbolj zahtevne meritve so bile meritve goriščne razdalje. Da bi čim bolje preverili za kakšne leče velja enačba leče, smo za vsako lečo izmerili kar se da veliko meritev pri različnih pozicijah leče glede na laserje.
Za preglednejše grafe definirajmo Δg kot odmik laserskega žarka na zaslonu (od gorišča) in Δs kot odmik žarka skozi lečo (od središča).
- Kondomska leča (napolnjena z vodo, f=18,4 cm)
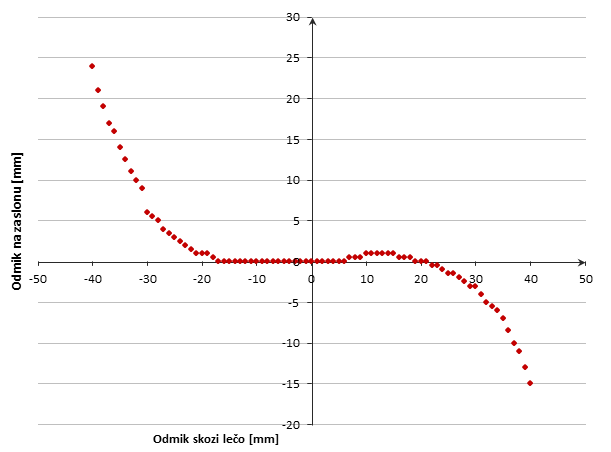
Graf 1: Δg(Δs) za kondomsko lečo.
Komentar: Iz grafa lahko ocenimo, pri katerih odmikih žarka skozi lečo še velja osnovna enačba leče. To se zgodi pri približno 20 mm odmika od središča leče.
- Mala leča (napolnjena z vodo, f=10,8 cm)
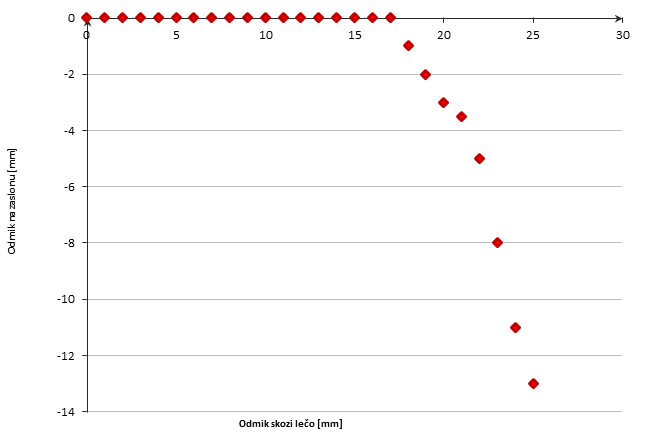
Graf 2: Δg(Δs) za malo lečo napolnjeno z vodo.
Komentar: Osnovna enačba leče preneha veljati pri približno 17 mm odmika od središča leče.
- Mala leča (napolnjena z oljem, f=10,8 cm)
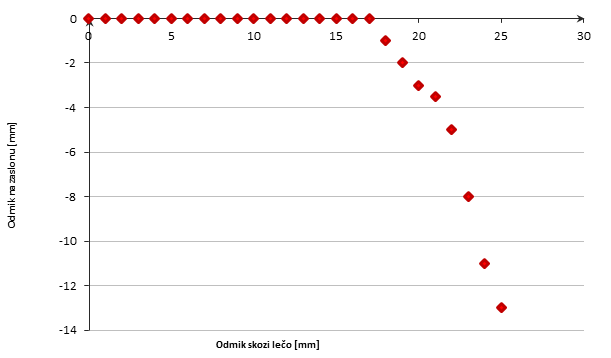
Graf 3: Odmika žarka na zaslonu (od gorišča) v odvisnosti od odmika žarka skozi lečo (od središča) za malo lečo napolnjeno z oljem.
Komentar: Osnovna enačba leče preneha veljati pri približno 17 mm odmika od središča leče.
- Velika leča (napolnjena z vodo, f=20,2 cm)
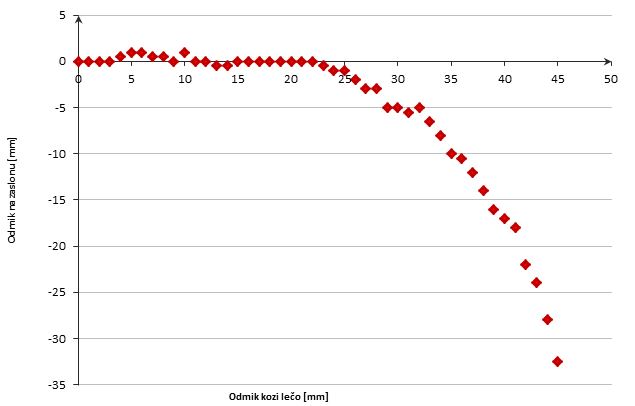
Graf 4: Δg(Δs) za veliko lečo.
Komentar: Osnovna enačba leče preneha veljati pri približno 26 mm odmika od središča leče.
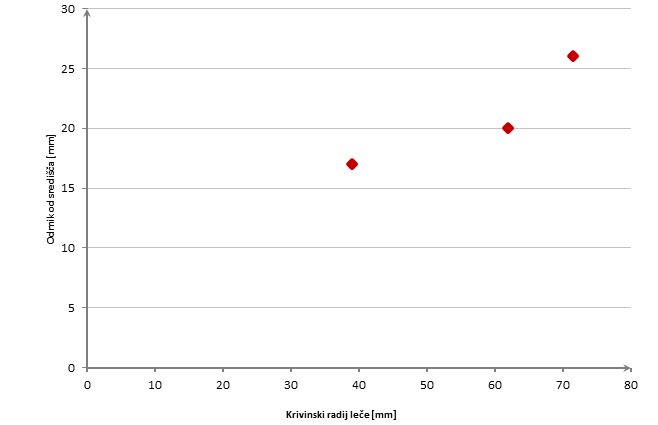
Graf 5: Δs pri katerem še velja enčba leče
Komentar: Iz grafa lahko vidimo, da odmik od središča, pri katerem še velja enačba leče, narašča s krivinskim radijem leče. Večja kot je leča, bolj se lahko odmaknemo od središča leče in še bo veljala enačba leče.
Na kazalo
Preizkus enačbe leče
Ker smo vse podatke izmerili smo se odločili preveriti še, kako goriščna
razdalja izračunana po enačbi leče sovpada z goriščno razdaljo, ki smo jo
določili fizično, z merjenjem oddaljenosti zaslona. Po formuli
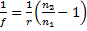smo izračunali goriščne razdalje in dobili
naslednje rezultate:
| Leča | Izmerjena goriščna razdalja [cm] | Izračunana goriščna razdalja [cm] |
|---|---|---|
| Mala leča (voda) | 10,8 | 12,6 |
| Mala leča (olje) | 10,8 | 11,8 |
| Velika leča | 20,2 | 23,1 |
| Kondomska leča | 18,4 | 20,0 |
Izmerjene in izračunane vrednosti zadovoljivo dobro sovpadajo. Absolutna napaka je največ 3 cm, kar približno sovpada z debelino leče in posledično napako goriščne razdalje. Mi smo goriščno razdaljo merili od vrha leče, saj smo s tem odpravili spreminjanje goriščne razdalje zaradi debeline leče (debelino leče smo spreminjali s tem, ko smo določali največjo oddaljenost od središča, pri kateri še velja enačba). Zaradi tega smo izmerili manjšo goriščno razdaljo, kot smo jo izračunali. Izmerjena goriščna razdalja je po naši oceni manjša od izračunane približno za toliko, kot je debelina leče, če za lečo vzamemo tako majhen del polkrožne leče, da se vsi žarki sekajo v gorišču.