Enačba leče

Projektno delo 2011

Kazalo:

• Krivinski radij
• Lom svetlobe
• Leče

Krivinski radij

Krivinski radij se lahko meri na različne načine. Mi smo uporabili dva različna. Za leče, narejene iz napolnjenih plastičnih hemisfer smo uporabili sferometer. To je priprava za merjeje krivinskega radija. Metoda merjenja temelji na meritvi višine krogelne kapice nad trikotnikom, ki ga določajo tri točke površja krogle. Radij tako izračunamo po enačbi:

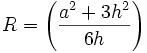
kjer je R krivinski radij, a razdalja med nogicami sferometra in h višina kapice.

Za lečo narejeno iz kondoma pa to ni mogoče, saj je površina preveč upogljiva in mehka. Zato smo se poslužili računalnika. Lečo smo slikali od strani in sliko obdelali v računalniku.

Radij krožnega loka leče dobimo z naslednjo enačbo:

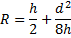
Enačbo dobimo s pomočjo izreka o tetivah, ki pravi, da je produkt dolžin A in B enak produktu dolžin C in D.

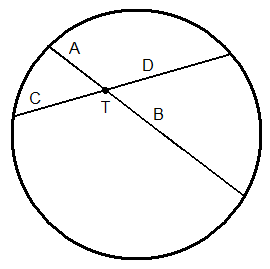
V našem primeru sta tetivi med seboj pravokotni, A je enak h dolžini C in D pa sta enaki polovici dolžine d. Po kratkem računu pridemo do zgornjega izraza.

Podatke smo pridobili z analizo fotografije v programu Logger Pro™. Za merilo smo imeli dolžino l, ki je premer petrijevke, čez katero je bila napeta leča.

Izmerjen premer posodice:	l = 9,1 cm
Pridobljene količine:	d = 8,7 cm h = 1,8 cm
Izračunan krivinski radij:	R = 6,2 cm

Na kazalo

Lom svetlobe

V različnih snoveh potuje svetloba z različnimi hitrostmi. V vakuumu potuje s stalno hitrostjo 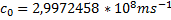, v snovi pa je hitrost svetlobe manjša. Razmerje med hitrostjo širjenja svetlobe v vakumu in v snovi imenujemo lomni količnik snovi.

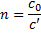
Pri čemer je n lomni količnik določene snovi, c' hitrost svetlobe v snovi in c₀ svetlobna hitrost v vakuumu.

Snov	Lomni količnik
zrak pri standardnih pogojih	1,0003
voda	1,33
steklo	1,5
kamena sol	1,54
ogljikov sulfid	1,62
diamant	2,4

Ker se pri prehodu iz prve snovi v drugo frekvenca ne spremeni, lahko lomni količnik zapišemo tudi kot razmerje valovnih dolžin:

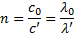
V enačbi λ' predstavlja valovno dolžino svetlobe v snovi, λ₀ pa valovno dolžino svetlobe v vakuumu.

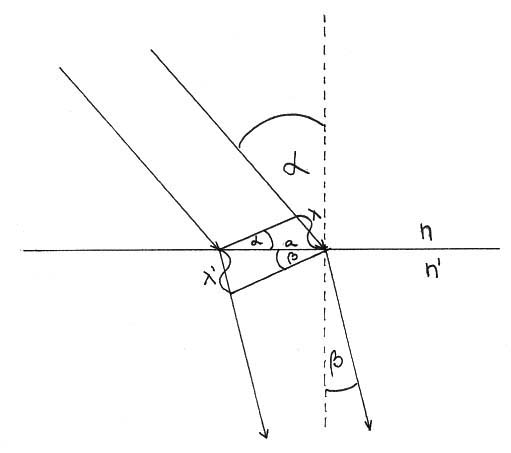
Zaradi različnih hitrosti v snoveh se svetloba pri prehodu iz ene snovi v drugo lomi. Lom je najlažje pokazati z dvema vzporednima žarkoma.

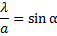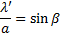Ko enačbi med sabo delimo, dobimo:

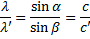
Če ulomek v števcu in imenovalcu množimo s c₀ (svetlobno hitrostjo v vakuumu), ugotovimo, da je razmerje sinusov vpadnega in lomnega kota kar enako razmerju lomnih količnikov snovi.

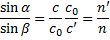
Snov z večjim lomnim koeficientom je optično gostejša (svetloba po njej potuje počasneje), snov z manjšim lomnim koeficientom pa je optično redkejša.

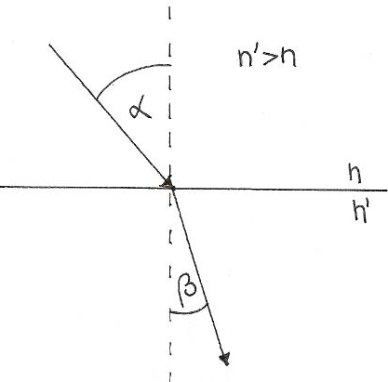
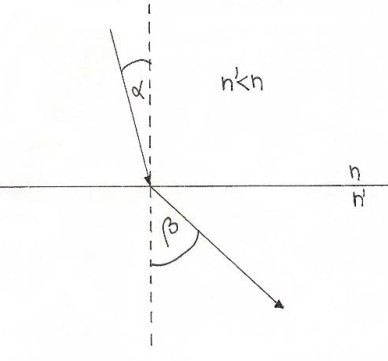
Ko svetloba prehaja v optično gostejšo snov, se žarek lomi proti vpadni pravokotnici, pri prehodu v optično redkejšo snov pa stran od nje.

V našem eksperimentu smo iz sinusov vpadnih kotov izračunali lomna količnika vode in olja.

Na kazalo

Leče

Pri geometrijski optiki zanemarimo uklon, interferenco in podobne svetlobne pojave ter se ukvarjamo samo z lomom in odbojem. V našem primeru smo se ukvarjali samo z lomom svetlobe v leči. Geometrijska optika je dober približek za računanje, kadar so žarki, mejne ploskve in ostale stvari, ki jih opazujemo, veliko večje od valovne dolžine svetlobe in lahko posledično »pozabimo« na uklon in interferenco.

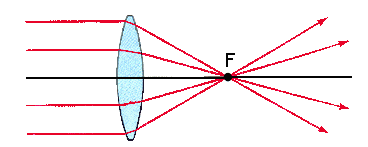
V našem primeru smo delali s krogelnimi, plankonveksnimi lečami. Krogelna plankonveksna leča je priprava iz prozorne snovi, ki ima na eni strani ravno ploskev, na drugi pa krogelno ploskev s krivinskim radiem r. Optično os določata normala na ravno ploskev in krivinsko središče ukrivljene ploskve. Žarek, ki leži v optični osi, pade na obe mejni ploskvi pravokotno in zato ne spremeni svoje smeri, žarki, ki so vzporedni z optično osjo in ležijo blizu nje pa se lomijo tako, da se sekajo vsi v isti točki – gorišču. Mi smo poskušali preveriti, kako blizu je blizu in kdaj spodaj napisana enačba leče velja, kdaj pa začne odstopati.

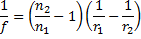
Predstavlja enačbo leče, ki jo bomo poskušali dokazati. V enačbi f predstavlja goriščno razdaljo leče, n₁ je lomni količnik sredstva, ki obdaja lečo, n₂ lomni količnik snovi iz katere je sestavljena leča, r₁ in r₂ pa sta krivinska radija leče. Pri delu s plankonveksnimi lečami se delo malo poenostavi. Krivinski radij ravne ploskve r₂ je neskončen, zato člen 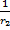izpade iz enačbe.

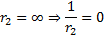
Za plankonveksno lečo velja torej enačba:

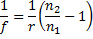
Pri čemer r nadomesti prejšnji r₁ in predstavlja krivinski radij ukrivljene ploskve.

Ker celoten eksperiment temelji na delovanju plankonveksne leče, bomo za lažjo predstavo njeno enačbo izpeljali. Enačba velja za tanke leče, majhne kote in velike krivinske radije.

-->

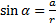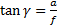
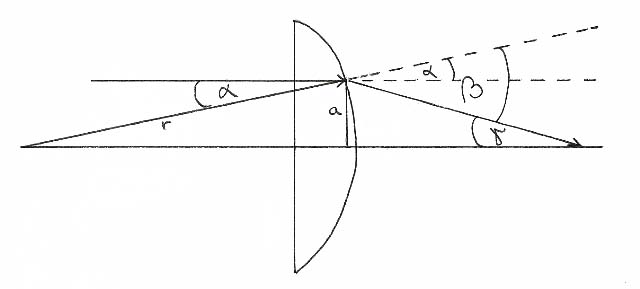
Sinus vpadnega kota α, označenega na skici, lahko izrazimo kot razmerje med oddaljenostjo žarka od optične osi in krivinskim polmerom leče, tangens kota γ, pa kot razmerje med oddaljenostjo žarka od optične osi in goriščno razdaljo leče. Že tukaj smo naredili manjšo napako pri merjenju goriščne razdalje, saj je v enačbi vzeta razdalja merjena od projekcije točke iz katere žarek izhaja iz leče na optično os, do gorišča. Če se omejimo na tanke leče (za katere zgoraj omenjena enačba velja), potem je ta napaka zanemarljiva. Ko enačbi delimo med sabo, dobimo:

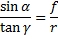
Ker smo se omejili na zelo majhne kote, lahko formuli za sinus in tangens razvijemo po taylorjevi vrsti do prvega člena in dobimo:

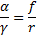
Če natačneje preučimo skico, pridemo do ugotovitve, da je kot γ enak razliki kotov β (kot pod katerim izstopi žarek glede na pravokotnico na lečo skozi točko, kjer je izstopil) in α (vpadni kot).

Ko v prejšnjo enačbo vstavimo γ=β-α in ulomek v števcu in imenovalcu delomo z α, dobimo naslednjo enačbo

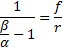
ki jo lahko preoblikujemo v obliko:

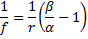
Iz teorije o lomu svetlobe vemo, da je razmerje sinusov vpadnega in lomnega kota enako razmerju lomnih količnikov snovi, kjer se svetloba lomi. Ker smo se omejili na majhne kote, lahko zapišemo kar sin⁡α=α in sin⁡β=β. Tako pridemo do enačbe:

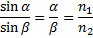
Ko to vstavimo v zgornjo enačbo, dobimo 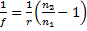, kar je ravno enačba, ki smo jo hoteli dokazati.

Ker smo v enačbi uporabili kar nekaj popravkov in nekaj dejstev zanemarili, bomo z eksperimentom poskušali pokazati, kdaj enačba res velja in kdaj začne odstopati.