Teorija

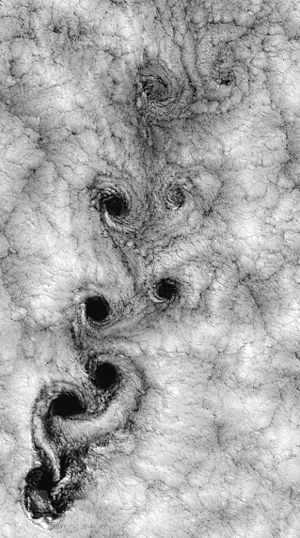
Animacija: von Karmanovi vrtinci

V animaciji so predstavljene tokovnice medija, ki obtekajo cilinder, pri predpostavki, da je medij sestavljen iz delcev. Črte so različno obarvane zaradi boljše preglednosti pojava; zaporedje treh barv predstavlja posamezne tokovne niti. Cilinder v tem primeru miruje, tokovnice pa imajo konstantno hitrost. Dogajanje je ekvivalentno enakomernemu gibanju cilindra.

Če predpostavka drži, se bo po nekem času vzpostavila tokovna turbulenca. Podobno situacijo dobimo, če na drogu visečo zastavo izpostavimo vetru; zaradi asimetrije tokovnic, cilindra in ostalih faktorjev veter palice zastave ne more obtekati simetrično. Zato je že majhna tlačna razlika dovolj, da sistem preide v turbulentno stanje. Vrtinci povzročijo po celotni dolžini cilindra spremembe v porazdelitvi hidrodinamičnega tlaka. Če imamo namesto nepremičnega cilindra lahko vrvico, ta pojav povzroči nihanje same vrvice. Nihanje povzroči zvok, ki ga slišimo pri rezanju zraka. Teorija von Karmanovih vrtincev se uporablja povsod, kjer se objekti premikajo skozi medij (npr: v avtomobilski, letalski, gradbeni industriji itd.).

Kliknite za povečanje slike

1. Turbulenca oblakov pri obtekanju visokega otoka
2. Polna razsežnost Karmanovih vrtincev (pogled iz vesolja)
3. Turbulenca pri mešanju barve z paličico

Spodaj zapisana enačba prikazuje soodvisne parametre, ki določajo lastnosti efekta turbulentnih vrtincev pri obtekanju cilindra.

Frekvenca nihanja ponazarja, s kakšno hitrostjo spreminja smer rezultanta sile hidrostatičnega tlaka. Pri naših meritvah ne bomo opazovali te frekvence, temveč njene posledice, zato enačba predstavlja situacijo pri idealnih pogojih (cilinder, ki ga enakomerno obtekajo tokovne niti). V našem primeru se hitrost spreminja po radiju, saj vrvico vrtimo okoli enega izmed njenih krajišč.

• 
• 
• 

Valovanje vrvice

Posledica von Karmanovih vrtincev je valovanje, ki ima veliko različnih frekvenc in amplitud. Predvsem zaradi različnih amplitud, ki se v tem primeru pojavijo zaradi kotne hitrosti (relativna hitrost glede na medij je odvisna od radija). Vsa ta valovanja interferirajo med sabo v vsiljeno valovanje vrvice. V našem primeru smo vrvico vrteli tako, da smo ji dodali utež na koncu; zato lahko rečemo, da je vrv idealno vpeta. Valovanje vrvice zaradi Karmanovih vrtincev potuje po vrvici, po nekaj trenutkih je na vrvici vzpostavljeno stalno valovanje. Zelo podobno situacijo dobimo pri vsiljenem nihanju vijolinske strune.

Videoposnetek prikazuje vzbujanje valov na struni violine. Z lokom potegnemo po struni; zaradi trenja se struna zagrabi za žico. Ko silo presežemo, struno izgubimo iz prijema loka, da vzvalovi. Frekvenca vzbujanja je zelo visoka in naključna, amplituda pa nizka. Po nekaj trenutkih se zaradi interference valovanje okrepi. Vzpostavi se valovanje z vsiljenimi frekvencami. Ob koncu vsiljenega nihanja se vzpostavijo stoječa valovanja.

Kliknite za prikaz videa...

Po teh enačbah lahko izračunamo glavne lastne frekvence niti. V našem primeru je valovanje sicer vsiljevano, vendar recimo da ni vsiljenega nihanja, to bomo primerjali z eksperimentalnimi podatki in ugotovili kako dobra je ta aproksimacija. Frekvenca zvoka, pri kateri doseže jakost zvoka maksimum, bo morala imeti valovno dolžino dvakrat večjo od same dolžine vrvice (prva lastna frekvenca).

Meritve bi morale potrditi izpeljano formulo iz zgornjih enačb:

Polni postopek izspeljave enačbe za izračun frekvence vrteče vrvice, če ne upoštevamo dušenja in vsiljenega nihanja.

Če rečemo, da je nihanje vsiljevano, moramo upoštevati resonančno krivuljo in njeno enačbo, ki nam bo pomagala pri razlagi eksperimentalnih meritev.

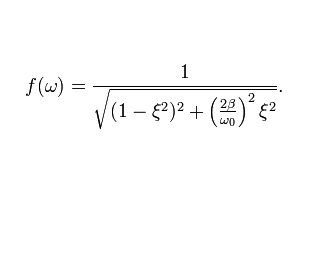
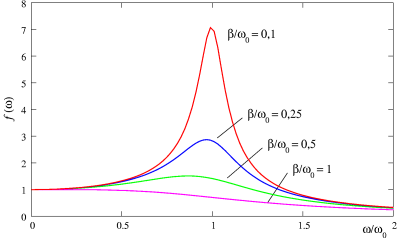
• ξ ... razmerje med vsiljeno in lastno frekvenco, ξ = ω/ω0.
• β ... pa koeficient dušenja.