Uvod v teorijo propagacije zvoka po segretih plasteh zraka
Širjenje zvoka po plinih (sem prištevamo tudi zrak), v okviru termodinamike obravnavamo kot adiabatni proces, saj smatramo spreminjanje razmer v mediju za nadvse hitro, kar nas napelje na misel da ni izmenjave toplote.
Za adiabatni proces velja naslednja zveza med tlakom in prostornino:
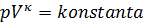
Tu je 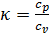
Iz tega pa sledita dve zvezi, ki ju lahko uporabimo za izpeljavo valovne enačbe, za širjenje zvoka v cevi.
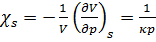
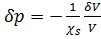
Osnova za izpeljavo valovne enačbe je kot velikokrat, drugi Newtonov zakon, ki ga zapišemo za stebriček zraka v cevi:
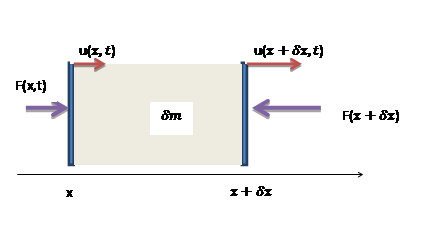
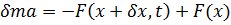
Postopek izpeljave valovne enačbe si lahko v splošnejši obliki ogledamo v vsakem univerzitetnem učbeniku za osnovni kurz klasične fizike, npr.
- David Halliday, Robert Resnick, Jearl Walker: Principles of Physics Extended, Ninth Edition, International Student Version
- Janez Strnad: Fizika 1. Del, Mehanika in Toplota.
Po postopku izpeljave, pridemo do take valovne enačbe:
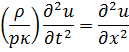
Izraz v oklepaju na levi je recipročna vrednost kvadrata hitrosti širjenja valovanja po plinih.
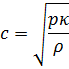
Gostoto izrazimo iz enačbe stanja za idealni plin:
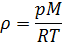
Kjer so M kilomolska masa, p tlak, R Raynoldsova konstanta, T pa temperatura.
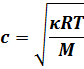
Vidimo, da je hitrost zvoka v idealnem plinu tem večja, čim višja je temperatura tega plina. Za realni plin, kar zrak tudi je, je enačba malce drugačna, a temperatura še vedno ostane v števcu pod korenom. Torej podčrtana ugotovitev še vedno obvelja.
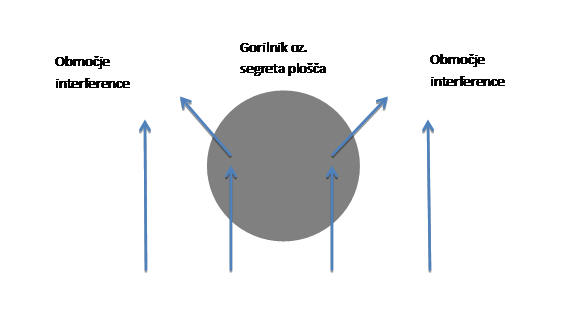
Posledica širjenja zvoka skozi segret zrak je uklon smeri širjenja valovanja. Nad močno segreto ploščo, se vzpostavi gradient temperature, ki kaže proti središču plošče (v to smer temperatura narašča). Ko zvok potuje prek plošče, se v plasteh zraka bliže središču plošče, hitreje širi. Zato se smer valovanja ukloni navzven.
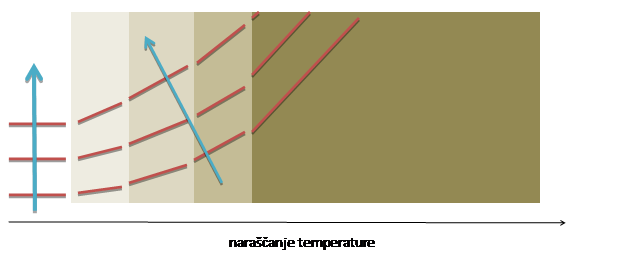
Zgornja shema prikazuje uklon smeri, pri širjenju zvoka na različno segretih plasteh zraka. Ko se dela zvočnega valovanja, ki prehajata preko različnih delov temperaturnega gradienta ponovno srečata, pride do interference, pri čemer dobimo značilne ojačitve, pod določenimi koti.
Pojav nekako oriše spodnja shema: