Uvod	Teorija	Eksperiment	Zaključek

Kapljevina

Kapljevina je zgoraj omejena z gladino, ta se obnaša kot tanka napeta prožna opna, ki lahko prenese manjše sile. Ta lastnost gladine je posledica sil med molekulami, ki sestavljajo kapljevino.

Molekula v površinski plasti kapljevine (z dosegom ) je obdana z manjšim številom molekul kot molekula v notranjosti kapljevine. Zato ima vsaka molekula v površinski plasti kapljevine večjo medmolekularno potencialno energijo kot molekula v njeni notranjosti.

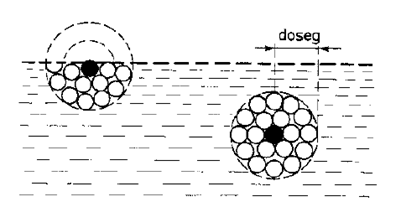
Premik molekule iz notranjosti kapljevine na gladino zato poveča njeno potencialno energijo. Ta prirastek potencialne energije površinskih molekul imenujemo površinska energija kapljevine  in je premo sorazmerna s številom molekul na gladini, to je s površino S gladine:

Sorazmernostni faktor  imenujemo površinska napetost, ki je odvisna od vrste snovi na obeh straneh proste gladine, pa tudi od temperature in primesi na gladini. Njena merska enota je

Površinska napetost kapljevine se z večanjem temperature zmanjšuje, z večanjem površine gladine pa zvišuje. Milo in različni detergenti zmanjšajo površinsko napetost vode, sol pa jo poveča.

Zaradi površinske napetosti se skuša površina gladine (vode, milnice…) čim bolj zmanjšati, saj se s tem najbolj zmanjša površinska potencialna energija. Geometrijsko telo, ki ima ob dani prostornini najmanjšo površino, je krogla. Zato se majhna množina kapljevine oblikuje v kroglo.

Dokaz za trikotnik

Imejmo trikotnik ABC s koti manjšimi od 120°. V tem trikotniku si izberimo poljubno točko in jo imenujmo P. To točko povežimo z oglišči A, B in C.
Naša naloga je poiskati tako točko F, da bo vsota dolžin daljic AF, BF in CF najkrajša.
Sedaj okrog oglišča B v pozitivni smeri zavrtimo trikotnik ABP 60°. Sliki točk A in P označimo s C' in P'.

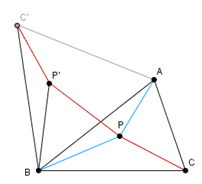
Ker je vrtenje okrog točke togi premik, sta trikotnika ABP in C'BP' skladna. Torej sta daljici C'P' in AP enako dolgi.
Opazimo, da sta rezultat vrtenja tudi enakostranična trikotnika AC'B in PP'B, zato sta tudi daljici P'P in BP enako dolgi.
Ugotovili smo, da velja: |AP| + |BP| + |CP| = |C'P'| + |P'P| + |PC|.

Razdalja, ki jo minimiziramo, je torej enaka dolžini poligonske poti od oglišča C do točke C', lomljene pri P in P'. Takšna pot, ki povezuje točki C in C' preko treh daljic, je najkrajša, če je ravna. To pa bo res le, če bo veljalo:

• kot BPC in kot BPP' tvorita iztegnjeni kot
• kot PP'B in kot C'P'B tvorita iztegnjeni kot

Za Fermatovo točko F mora torej veljati:

• kot BFC = 180° - kot BFF' = 120°
• kot AFB = kot C'F'B = 180°- kot FF'AB= 120°

To pa pomeni, da je Fermatova točka tista točka, iz katere vsako izmed stranic trikotnika ABC vidimo pod kotom 120°.
Opazimo še, da je štirikotnik FAC'B tetiven, saj je vsota nasprotnih kotov tega štirikotnika enaka 180°. Torej mu lahko očrtamo krožnico. Sedaj vemo, da je Fermatova točka presečišče daljice CC' in krožnice, očrtane enakostraničnemu trikotniku nad stranico AB in je s tem enolično določena.

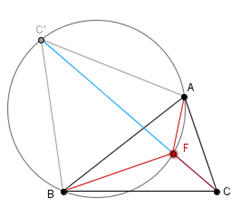
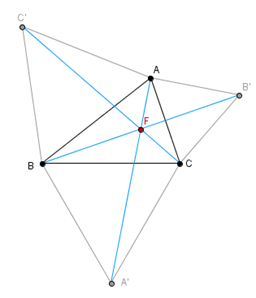
Namesto vrtenja okrog oglišča B bi pravtako lahko vrteli okrog oglišč A in C. Tako bi dobili tri enakostranične trikotnike, nad vsako stranico enega. Tako dobljene daljice AA', BB' in CC' so enako dolge in se sekajo v Fermatovi točki, ki je seveda tudi presečišče krožnic, očrtanih enakostraničnim trikotnikom nad stranicami trikotnika ABC.

V trikotniku s kotom večjim ali enakim 120° je Fermatova točka vrh največjega kota.

Dokaz za kvadrat

Recimo, da imamo podan kvadrat z dolžino 1, milna opna pa zavzame naslednjo obliko, kjer so m, n dolžine označenih razdalj in kot Θ :

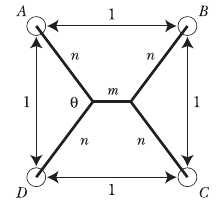
Opomba: n je enak po dolžini 4 odsekom milne opne zaradi simetrije njene oblike, ki jo zasede.
Mi želimo dokazati, da je ta oblika milne opne najkrajša.
Naj bo L celotna dolžina milne opne, torej  . Poiščimo sedaj dolžino n. V ta namen konstruirajmo naslednji pravokotni trikotnik, kjer  sta kateti dolžin  in p, hipotenuza pa je dolžine n:

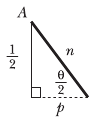
Iz tega pravokotnega trikotnika sledi:     in   .
Iz pitagorovega izreka sledi:     oz.  .
Vstavimo n in dobimo:  , ker je .
Ker je  , je potem  .
Sedaj lahko zapišemo še L:
Da poiščemo kot , ki minimizira L, moramo najprej najti :
 .
Nato poiščemo minimum  , tako da rešimo enačbo   oz.  .

Z malce računanja hitro ugotovimo, da je  .
Tako ugotovimo, da je kot  tisti, pri katerem je razdalja L najmanjša. Tudi pri naših eksperimentih se izkaže, da je kot, ki ga napenja naša milna opna tudi , iz tega torej sledi, da milna opna res zavzame najmanjšo možno razdaljo.

Povzeto po članku A mathematical solution to the motorway problem, napisal ga je Matthew T. Michaelson, v reviji Australian Senior Mathematics Journal 23(2)

Minimalna pot med danimi n točkami

Imejmo v ravnini n točk. Cilj je povezati vse točke z najkrajšo možno potjo, pri tem pa lahko dodamo poljubno točk, če nam to pripomore k zmanjšanju vsote skupnih razdalj. Ta problem je definiral Jacob Steiner, zato se mu tudi reče Steinerjev problem, točke, ki jih dodamo grafu pa Steinerjeve točke.

Kot rezultat zmeraj dobimo drevo, ki mu rečemo tudi Steinerjevo drevo. Za dano množico točk obstaja več Steinerjevih dreves.

Za n=3 Steinerjeva točka sovpada s Fermatovo točko.

Pomembna dejsta o Steinerjevih drevesih:

1.) Vsaka Steinerjeva točka je stopnje 3

• Stopnja točke je število povezav
• Več informacij o tem, kaj je stopnja točke, najdete tukaj.

2.) Kot med daljicami v Steinerjevih točkah je 120°

3.) Za danih n točk je kvečjemu n-2 Steinerjevih točk