Uvod	Teorija	Eksperiment	Zaključek

Kljub začetnim problemom dejanskega namena in razumevanja naloge, smo uspešno preučili vse zahtevane aspekte le-te.
Na izdelani napravi smo preizkusili različne like, kjer smo dobili rezultate, ki se ujemajo s teorijo. Prišli smo do osupljive ugotovitve, da teža ne vpliva na obliko milne opne, saj se le ta po nekaj sekundah vrne v začetni položaj kljub različnim koncentracijam raztopine.
V teoretičnem delu poročila smo eksplicitno dokazali, da milna opna zavzame najmanjšo površino, le za trikotnik in kvadrat. Ob proučevanju problema, smo naleteli na zanimivo teorijo, ki je dejansko teorija našega problema. To so Steinerjeva drevesa. Presenetilo nas je tudi dejstvo o neenoličnosti Steinerjevih dreves, kar lahko vidimo v eksperimentalnem delu za štirikotnik. Tam se milna opna v dveh različnih poskusih napne na dva različna načina, vendar sta obe formaciji Steinerjevi drevesi, torej lahko govorimo o zavzetju lokalnih minimumov.

Za konec si lahko ogledate še slike, ki smo jih obdelali z zastonjskim programom GeoGebra 4.0, kjer smo želeli ugotoviti lastnosti Steinerjevih minimalnih dreves. Stopinje so zaokrožene na eno decimalko.

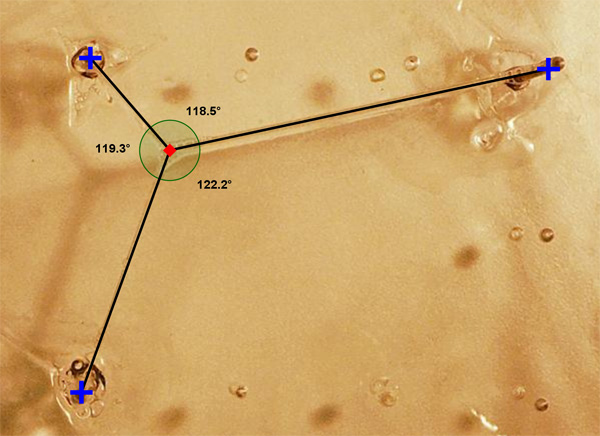
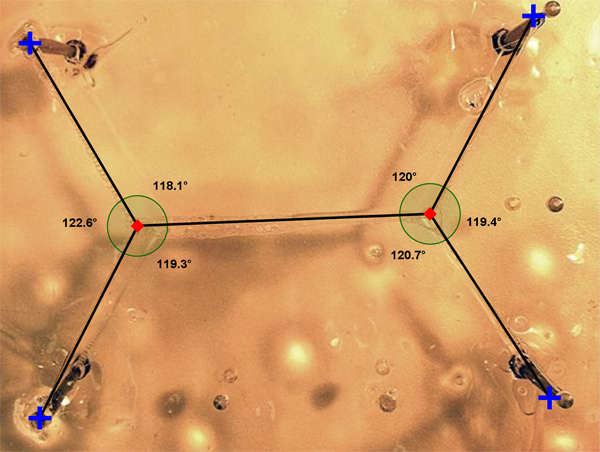
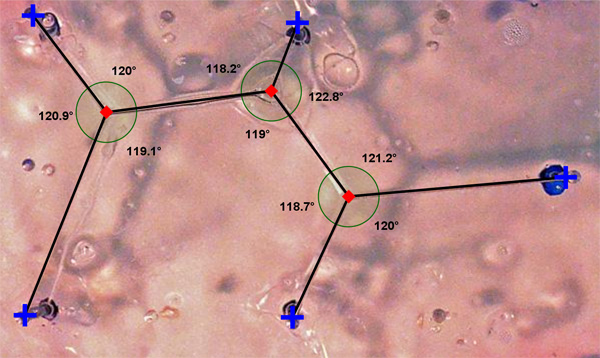
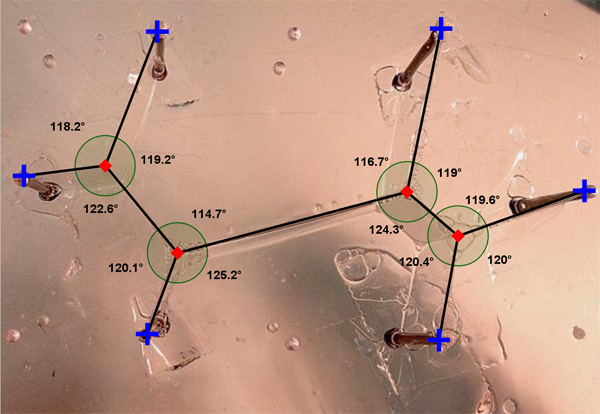
Kot lahko vidimo, res velja, da je vsaka Steinerjeva točka stopnje 3, prav tako vidimo, da so koti med daljicami, ki gredo iz Steinerjevih točk, res 120°. Do minimalnih napak pride zaradi projekcije slike in/ali zaradi nagnjenosti fotoaparata. Prav tako velja tudi trditev (vsaj v naših primerih), da se za N točk v ravnini doda N-2 Steinerjevih točk.

Morda bi koga še zanimalo dinamično raziskovanje Steinerjeve točke na primeru trikotnika, zato smo še naložili na splet en majhen applet. POZOR: za izvajanje appleta potrebujete vtičnik Java v vašem brskalniku. Dobite ga tukaj.

Steinerjeva točka v trikotniku s programom GeoGebra

Možne izboljšave: Problem so nam delali žeblji, ki so padali iz spodnje pleksi plošče, zato smo jih zalepili z lepilnim trakom. Naprava bi bila boljša, če bi žeblji sami stali v plošči, vendar nam je tudi z našo napravo uspelo narediti milne opne.

Viri:

[1] http://en.wikipedia.org/wiki/Steiner_tree_problem

[2] http://www.archive.org/details/RonaldLG1988

[3] http://www.eric.ed.gov/PDFS/EJ867341.pdf

[4] Janez Strnad, FIZIKA, prvi del, DMFA