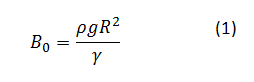
Bondovo število [2] je brezdimenzijska količina, s katero opišemo, kako pomembne so sile površinske napetosti v primerjavi z ostalimi volumskimi silami na telo. To so sile, ki delujejo po celotni prostornini telesa, na primer elektromagnetna sila in sila gravitacije. Nas bo zanimalo, kako pomembna je sila gravitacije. Za Bondovo število velja:
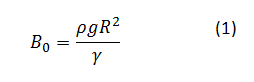
kjer je ρ gostota tekočine, γ površinska napetost, g gravitacijska konstanta in R karakteristična dolžina. Karakteristična dolžina je radij krogle s prostornino enako prostornini naše kapljice. Če je Bondovo število visoko, to pomeni, da ima površinska napetost majhen vpliv na opazovan sistem. Če je B0<1, prevlada vpliv površinske napetosti nad gravitacijo.
Natančen geometrijski opis zamrzovanja kapljice je zelo zapleten, zato se bomo problema lotili s poenostavljenim modelom. Namesto da bi upoštevali realno obliko kapljice, ki zavisi od zunanjih pogojev, bomo predpostavili, da ima kapljica na začetku obliko odrezane krogle. Proces zamrzovanja, premikanje mejne ploskve med trdno in tekočo fazo vode bomo poenostavili tako, da vzamemo, da je mejna ploskev med ledom in vodo ravna in vzporedna s podlago ter da se pri dviganju prilagaja začetni obliki kapljice in se ne širi v radialni smeri. Kotu ϑ na sliki bomo rekli kontaktni kot.
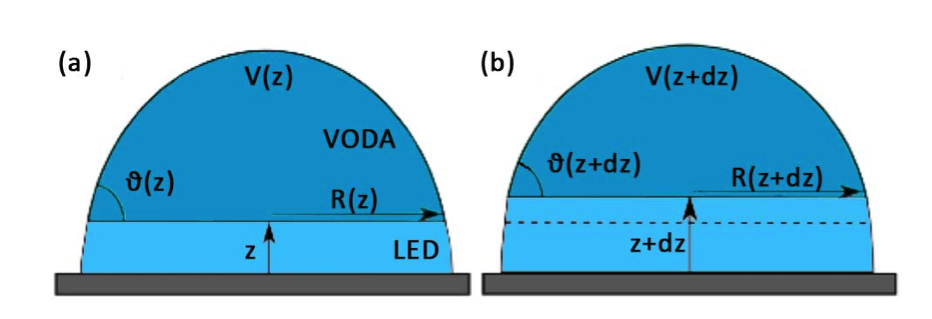
Slika 2: Geometrijski model zmrzovanja vodne kapljice na mrzli podlagi. (a) Privzamemo, da je meja med ledom in vode vodoravna in da ima kapljica na začetku obliko odrezane krogle. Pri tem je R polmer nezmrznjenega dela, V prostornina vode in ϑ kontaktni kot. (b) Predpostavimo, da ledena plast zavzema obliko ledene kapljice.
S pomočjo takega modela dobimo rezultate, ki opišejo pojav singularnosti pri zamrznitvi kapljic. Pokazali bomo, da to velja le za nekatere od tistih tekočin, ki imajo v trdnem stanju manjšo gostoto kot v kapljevinastem. Dobili bomo tudi približno oceno za razmerje gostot trdnega in kapljevinastega stanja za snovi, pri katerih je pojav še opazen. Začetne predpostavke oziroma poenostavitve vplivajo na rezultat v tolikšni meri, da dobimo koničast vrh le za relativno nizka razmerja gostot. Rezultat izključi vodo iz množice tekočin, primernih za ta pojav, kar pa se ne sklada z eksperimentom. Rezultat torej ne bo popolnoma konsistenten z našimi opazovanji, vendar bo kljub vsemu prikazal postopek tvorbe singularnosti in osnovno fizikalno podlago pojava. Glavna prednost poenostavljenega modela je v tem, da je matematično relativno enostaven in v celoti analitično rešljiv.
Model vsebuje tri geometrijske parametre, ki so odvisni od višine mejne plasti med trdnim in kapljevinskim stanjem in jo označimo z z. Radij zgornje ploskve ledenega dela bomo označili z R, prostornino kapljevinastega agregatnega stanja z V in kontaktni kot z ϑ Kapljice bodo, preden zamrznejo, zavzele obliko krogelne kapice. Z izbranimi parametri lahko izračunamo normalizirano prostornino kapljevinaste krogelne kapice nad ledeno plastjo,
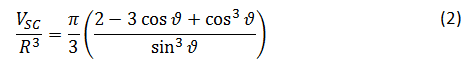
s katero dobimo zvezo med omenjenimi parametri V, R in ϑ. Indeks SC pomeni prostornino krogelne kapice: angleško ”spherical cap”.
Z upoštevanjem predpostavke, da se kapljica med zmrzovanjem ne širi v radialni smeri, dobimo razmerje med kotom ϑ, ter med strmino zaledenelega dela kapljice:
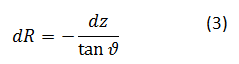
Med procesom zmrzovanja se mora masa vode ohranjati. To pomeni, da se z povečevanjem mase ledu dm=ρsdVs, zmanjšuje masa vode v kapljevinastem stanju dm=-ρldV. Pri tem sta ρs in ρl gostoti vode v trdnem (solid) in kapljevinstem (liquid) agregatnem stanju. Upoštevamo še, kako se s spremembo višine spremeni prostornina ledene plasti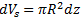 
in dobimo:
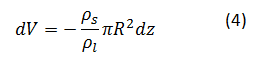
Enačbi (3) in (4) zapišemo kot diferencialni enačbi, s katerima opišemo celoten model:
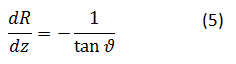
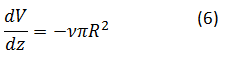
Pri tem smo vpeljali nov parameter ν=ρs⁄ρl, gostotni količnik, ki je enak razmerju gostot vode v trdnem in v kapljevinastem stanju. Z diferenciacijo enačbe (2), ter z upoštevanjem enačb (5) in (6), lahko dobimo nov sistem diferencialnih enačb za R in ϑ:
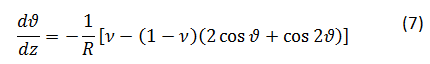
Sitem je za R(ϑ) povsem analitično rešljiv, vendar je proces izpeljave enačbe za splošen gostotni količnik ν nekoliko zapleten. Obravnavali bomo limitno vrednost ν=1, ko sta gostoti trdnega in kapljevinastega agregatnega stanja enaki. Enačbi (7) in (8) lahko potemtakem zapišemo kot
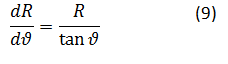
Po integraciji dobimo:
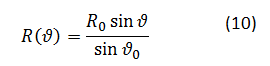
kjer sta R0 in ϑ0 radij ter kontaktni kot na stiku kapljice s podlago pred začetkom zmrzovanja. Rešitev je krogla z radijem R0⁄sin(ϑ0) . Tako rešitev dobimo, ker pri vrednosti ν=1 ne pride do povečanja prostornine kapljice, kar pomeni, da tudi oblika po zamrznitvi ostane enaka.
Enačb (7) in (8) se bom lotili še na drug način. Z numerično integracijo dveh diferencialnih enačb lahko dobimo lep grafičen prikaz predvidene oblike zaledenele kapljice. Pri integraciji si bomo pomagali s programom Mathematica, lahko pa uporabimo katerikoli drug podoben program. Na Sliki 4 sta prikazana dva grafa, ki ustrezata različnim kontaktnim kotom med kapljico in podlago.
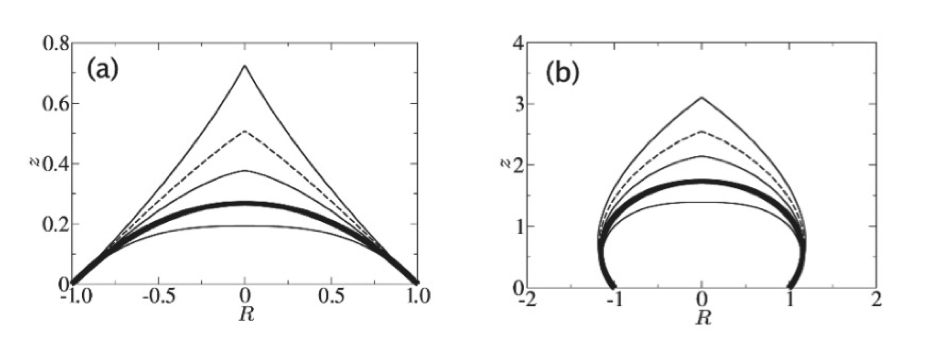
Slika 3: Numerične rešitve modela ledenih kapljic. (a) Hidrofilna površina z začetnim kontaktnim kotom ϑ=30°. (b) Hidrofobna površina z začetnim kontaktnim kotom ϑ=133,5°. Prikazane so krivulje pri različnih gostotnih količnikih, od zgoraj navzdol: ν=0,65, ν=0, 75, ν=0,85, ν=1, ν=1,2, pri začetnem radiju R0=1. Debela polna črta predstavlja kapljico pri ν=1, črtkana črta pa kapljico pri kritični vrednosti gostotnega količnika (ν=3⁄4). Oblike izgledajo nekoliko sploščene zaradi različnih skal na oseh.
Grafa prikazujeta oblike ledenih kapljic za tekočine z različnimi gostotnimi količniki. Najprej si poglejmo primer, ko je gostota snovi v trdnem agregatnem stanju enaka gostoti v kapljevinastem. Gostotni količnik je torej ena, kar je na primeru prikazano z debelo polno črto (Slika 4). Črta se ujema s krožnim odsekom, čeprav na grafu zaradi različne izbire skal, to ni očitno. Rezultat za primer ν=1 se torej ujema z napovedjo, tako kot tudi z analitično rešitvijo. Poglejmo si ostale krivulje. Čim manjši je gostotni količnik, tem bolj špičast je vrh kapljice, ko kapljica v celoti zmrzne. Analitična rešitev pokaže, da obstaja neka kritična vrednost νc, pri kateri je še opazen prelom krivulje in pri katerem je nastalemu stožcu še mogoče določiti kot ob vrhu. Ko omenjamo stožec, govorimo o nastali konici oziroma delu, ki je relativno blizu samega vrha kapljice. To je razvidno iz Slike 5. Pokazali bomo, da je za naš poenostavljen model, kritična vrednost pri νc=3⁄4.
Za količnike, večje od kritične vrednosti je vrh kapljice zaobljen. Čim večji je gostotni količnik, tem bolj je oblika ledene kapljice podobna krogli (ν=1). Okroglina se ohranja tudi za količnike, večje od 1. To pomeni, da ima snov v kapljevinastem agregatnem stanju nekoliko manjšo gostoto kot v trdnem. V tem primeru dobimo kapljico, ki bi se po prehodu v trdno stanje nekoliko sploščila v elipsasto obliko.
Dobljene rešitve sicer spominjajo na rezultate poskusa, vendar hitro ugotovimo, da se z rezultati numerično ne ujemajo. Za odstopanja so odgovorne začetne predpostavke oziroma poenostavitve problema. Predstavljen numerični model tvori špico pri gostotnem količniku, ki je enak ali manjši od ν=3⁄4. Če bi to držalo tudi v naravi, bi vodna kapljica z gostotnim količnikom ν=0,9, pri prehodu v trdno agregatno stanje, ostala zaobljena. Površina bi se sicer nekoliko dvignila, vendar ne bi tvorila ostre konice.
Slika 4: Grafični prikaz nastanka stožca. Da bi dobili oster vrh kapljice, mora biti masa snovi v kapljevinastem stanju enaka masi snovi v stanju, kjer tvori stožec. To se pojavi še v primeru, ko ima kapljevina večjo gostoto kot snov v trdnem stanju. Gostotni količnik mora biti manjši od kritičnega ν<νc=3⁄4.
S kompleksnejšimi matematičnimi modeli, ki v izračunih upoštevajo še mnoge druge parametre, katerih vpliv smo v našem primeru zanemarili, se lahko bolj približamo merskim rezultatom. Z upoštevanjem vplivov gravitacije, kapilarnega dviga, spreminjajočega se stičnega kota med tremi agregatnimi stanji in termodinamike znotraj kapljice, se lahko zelo dobro približamo eksperimentalnim izmerkom. V članku [4] je predstavljena poglobljena in kompleksnejša različica našega modela, ki dejansko da rezultate, primerljive z eksperimenti.
Naš model torej kvantitativno ne opiše pojava, toda kvalitativno toliko bolj nazorno predstavi bistvo pojava in s tem pojasni primer tvorbe singularnosti.
Povejmo še nekaj o različnih podlagah in kako, če sploh, kasneje to vpliva na obliko ledene kapljice. Od snovi iz katere je podlaga je močno odvisno, kakšno obliko bo voda zavzela. Če bomo kapljico spustili na hidrofilno površino, bo kontaktni kot s podlago manjši, kot če je podlaga hidrofobna. Slika 4 prikazuje oba primera pri kotih ϑ0=30° in ϑ0=133,5°. Oblika spodnjega dela že zamrznjene kapljice bo očitno odvisna od podlage. Zanima nas, kako to vpliva na zgornji del kapljice oziroma na špico, ki se tvori na vrhu. Izkaže se, da oblika špice ni odvisna od kota s podlago, ne glede na gostotni količnik ν. Izjema je le kritična vrednost νc, kjer pride do malenkostnih odstopanj.
Naslednji korak je napovedovanje kritične vrednosti razmerja gostot νc na podlagi teoretičnega modela. Najti moramo način, kako podrobneje opisati vrh oziroma špico ledene kapljice. Glede na rezultate modela pričakujemo tri ločene primere. Ko je ν<νc, po zamrznitvi dobimo koničasto ledeno kapljico. V drugem primeru, ko je ν>νc, ostane kapljica zaobljena skozi celoten proces zmrzovanja. Ostane nam kritični primer, ko je ν=νc. Numerični model za obravnavo le te ni najboljša izbira, saj bi morali močno zmanjšati korak pri računanju točk blizu vrha in s tem povečati število izračunov. Izkaže se, da lahko v veliko primerih neposredno bližino singularnosti obravnavamo povsem analitično, četudi v sami točki problem nima rešitve. V ta namen vpeljemo novo spremenljivko, ki ponazarja, kako blizu singularnosti se nahajamo. Opišemo torej odmik od točke, v kateri rešitev modela ni definirana in računamo v limiti, ko gre odmik proti nič. Za naš primer bomo vzeli maksimalno višino ledene kapljice in jo označili z z0. Odmik od najvišje točke nato zapišemo kot
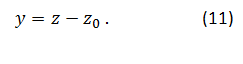
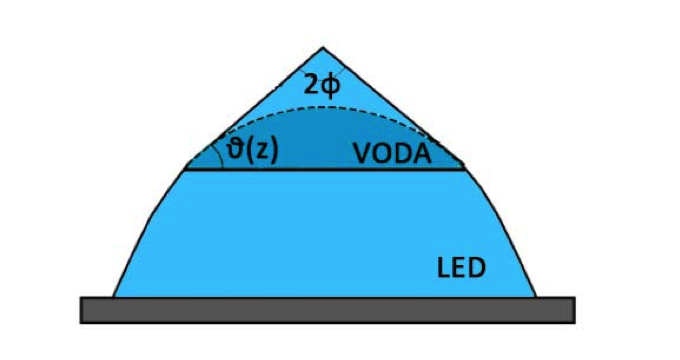
Obravnavali bomo obliko kapljice, ko gre y→0. Zgornji del ledene kapljice bomo opisali s pokončnim stožcem s kotom 2φ ob vrhu. Pokazali bomo, da je velikost kota φ odvisna le od gostotnega količnika. Če uporabimo še prej vpeljani y, lahko obliko stožca opišemo z enačbo R=y tanφ. Kot φ je odvisen od tega, na kateri višini znotraj kapljice predpostavimo stožčasto obliko. Lahko ga povežemo s kotom φ, ki je na višini z kot med ravno ploskvijo ledenega dela in strmino stene kapljice. Velja ϑ=π⁄2-φ. Zveza je konstantna, saj je φ neodvisen od višine z.
Na novo vpeljano spremenljivko y uporabimo pri integraciji enačb (5) in (6) in dobimo:
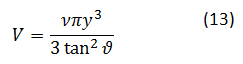
Druga enačba nam pove prostornino vode potrebne, da zapolnimo leden stožec. Zapišemo jo še drugače:
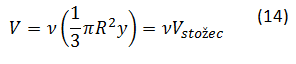
Namesto faktorja (y⁄tanϑ)^2 smo vstavili R^2. Izraz v oklepaju je ravno definicija prostornine stožca, če jo pomnožimo z gostotnim količnikom. Dobimo ustrezno prostornino kapljevinastega stanja. Pri iskanju kritične vrednosti si bomo pomagali z grafično predstavitvijo, zato v ta namen enačbo (13) zapišemo v brezdimenzijski obliki:
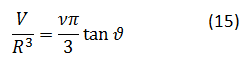
Iz Slike 2 je razvidno, da mora biti masa ledu v stožcu enaka masi vode v delu krogle, obarvanem s temno barvo. Pri danem razmerju gostot ν, tem pogojem ustreza en sam kot ϑ. Dobimo ga s primerjavo obeh mas ρlVSC=ρsVcone, oziroma s primerjavo prostornine krogelnega dela in prostornine stožca iz enačbe (13) ali (14) VSC=V. Rešitve so prikazane na grafu (Slika 5).
Normalizirana prostornina krogelnega dela po enačbi (2) je na grafu prikazana z debelo polno črto. Ostale krivulje pripadajo enačbi (15). Prikazane so normalizirane prostornine ledenega stožca pri različnih gostotnih količnikih. Iz grafa je razvidno, de le tanka polna črta seka črto normalizirane prostornine krogelnega dela. To pomeni, da izmed treh prikazanih razmerij gostot, le pri ν=0,6 najdemo želeno rešitev, to je kot ϑ, pri katerem je izpolnjen pogoj enakosti mas.
Pri krivuljah, ki pripadajo količnikom ν, večjim od kritičnega νc;, do presečišča ne pride. Tekočine s temi lastnostmi torej ne tvorijo ostre konice. Kako torej po vsem tem določimo kritično vrednost? Zanima nas, kdaj bo prostorninska krivulja stožca tangentna na krivuljo krogelnega dela. Izračunajmo naklona obeh krivulj pri kotu ϑ=0. Odvajamo enačbi (2) in (15) pri čemer dobimo V';SC;(0)=π R^3⁄4 in V'(0)=νπ R^3⁄3. Prostornini se ujemata pri kritični vrednosti gostotnega količnika νc=3⁄4.
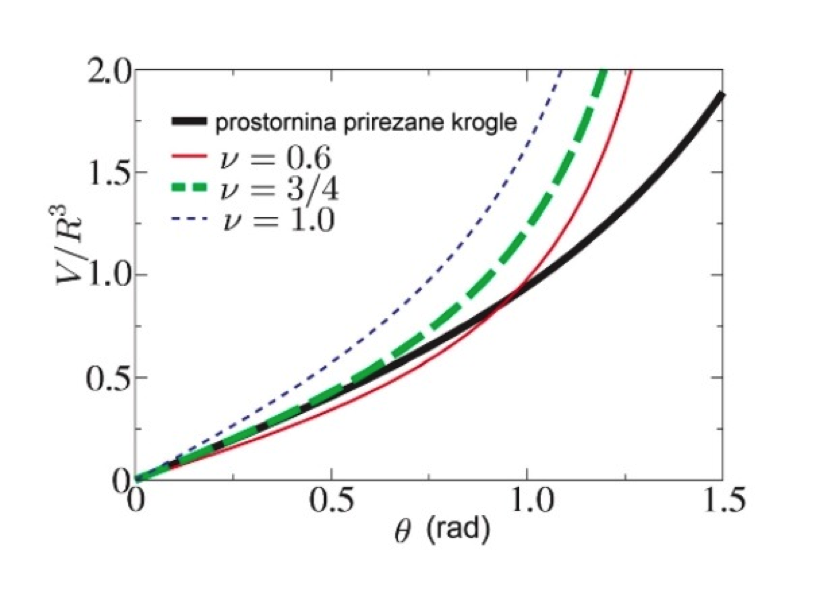
Slika 5: Predstavitev normalizirane prostornine V⁄R^3 v odvisnost od kota naklona. Debela polna črta prikazuje normalizirano prostornino kroglaste kapljice po enačbi (2); ostale krivulje prikazujejo normalizirane prostornine po enačbi (15). Dve krivulji se, raz en pri kotu nič, sekata le za ν=3⁄4.
Ko vodna kapljica v celoti zmrzne tvori oster koničast vrh. Tam se začnejo nabirati kristalčki, ki kmalu pokrijejo celotno ledeno kapljico. Poskus še nekajkrat ponovimo in opazimo, da se rast kristalov vedno začne ravno na ostrem delu, se pravi na vrhu kapljice. To je lep primer pojava, ki mu v angleščini pravijo "edge effect", robni pojav.
Pri študiju dinamike snežink je posebno pomembna teorija difuzijsko omejene agregacije, ki sta jo prva vpeljala ameriška fizika T.A. Witten in L.M. Sanders leta 1981. Najpomembnejša ideja te teorije je, da je rast kristalčka v snežinko odvisna zgolj od lokalnih lastnosti površine kristala, saj molekule vode nanjo udarjajo ena za drugo in se prej ne sprijemajo v skupke. Različni deli te površine pri rasti praktično ne interagirajo med sabo. Pri rasti snežink so zelo pomembni deli kristala z majhnim krivinskim radijem, oziroma tisti, ki so najbolj špičasti kot bi lahko tudi rekli. V ostro zamejenih, majhnih prostorčkih na površini ledenega kristala, ki se spreminja v snežinko, se namreč rada kondenzira voda v kapljevinasti obliki, ki nato deloma zamrzuje in omogoča rast kristala. Da se takšni procesi pri rasti snežink res dogajajo nam izpričuje tudi velika podobnost med končno obliko računalniško simuliranih snežink in tistih, ki jih lahko zares opazimo v naravi.
Vrnimo se na primer z zamrznjeno vodno kapljico. Edino, kar omejuje nastajanje ledenih kristalčkov na že zaledeneli površini, je učinkovitost transporta molekul vodne pare. Zato pričakujemo, da je rast kristalov najhitrejša na delih, kjer je največja difuzija. Za vodno paro okrog naše kapljice predpostavimo, da velja difuzijski zakon,
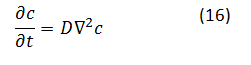
pri čemer je c koncentracija vodne pare v okolici kapljice in D difuzijska konstanta. Privzemimo, da se okolica ne spreminja s časom, a dopušča izmenjavo energije. Pravimo, da je v kvazi-stacionarnem stanju. Uporabimo lahko Laplaceovo enačbo:
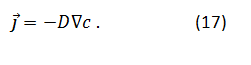
Če je koncentracija vodne pare blizu kapljice konstantna, bo problem ekvivalenten problemu z električnim potencialom okrog prevodne konice. Na tem mestu poglejmo Sliko 6, ki lepo prikaže model koncentracije vodne pare v okolici ostre konice. Razvidno je, da se okoli konice ustvari velik gradient koncentracije vodne pare. To pomeni, da bo na mestu okoli konice transport vodnih molekul najhitrejši, in se bo tvorba ledenih kristalčkov začela prav tam. Opisali smo poenostavljen model. Sicer je celoten pojav bolj kompleksen, saj je parni tlak nad ravno površino drugačen kot nad ukrivljeno površino.
Ocenimo še hitrost širjenja ledene plasti oz. kako je debelina ledu odvisna od časa. Imamo podlago s konstantno temperaturo T0, zaradi katere kapljica začne zmrzovati. Ob stiku s podlago se začne tvoriti plast ledu, ki se širi proti vrhu, dokler cela kapljica ne zaledeni. Nad to plastjo je voda v kapljevinastem stanju s temperaturo T1. Privzamemo, da se toplota prevaja enodimenzionalno skozi ledeno plast in da ledena plast ostaja vodoravna. Plast vode tik nad ledeno plastjo je v termodinamskem ravnovesju z ledom, zato je njena temperatura T1=0ºC. Ker ima voda v našem primeru višjo temperaturo kot podlaga, teče toplota skozi ledeno plast, kar opišemo z enačbo:
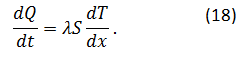
Pri tem je λ toplotna prevodnost ledu, S površina ledene plasti, dT temperaturna razlika med podlago in vodo nad ledeno plastjo in dx je debelina ledene plasti. Če privzamemo konstantno razliko temperatur dT=ΔT in konstantno debelino ledene plasti dx=Δx=h, lahko zapišemo:
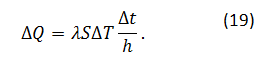
Odtekanje toplote povzroči, da nekaj vode zmrzne, pri čemer velja ΔQ=mqt, m je masa vode, ki zmrzne in qt specifična talilna toplota. Enačbo zapišemo v obliki
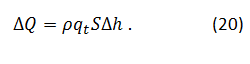
Pri tem nam Δh pove, za koliko se ledena plast odebeli. Z izenačitvijo enačb (19) in (20), po diferenciaciji in integraciji pridemo do enačbe, ki nam opiše časovno spreminjane debeline ledene plasti:
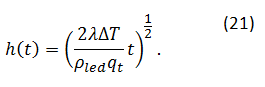
Izkaže se, da na hitrost zmrzovanja vpliva tudi kontaktni kot kapljice s podlago. Čim večji je kontaktni kot, daljši je čas zmrzovanja, saj je pri enaki količini vode kapljica višja. Kar je zanimivo je, da je tudi rast kristalčkov na površini kapljice, ki je zmrznila na hidrofobni podlagi, hitrejša. Kristalčki so bolj razvejani in večji.
Slika 6: Tvorba ledenih kristalčkov. (a) Fotografija konice, ko je kapljica že v celoti zamrznjena. Ostra konica predstavlja točko, kjer se začne zbirati vodna para, ki tvori ledene kristalčke. (b) Matematični model koncentracije vodne pare okrog konice. Bele črte so črte konstantnih koncentracij. Vidimo, da so blizu konice črte bolj skupaj, kar pomeni, da je tam velik gradient koncentracij. Tam se začne vodna para kopičiti in tam se začnejo tvoriti kristalčki.