OBDELAVA IN ANALIZA MERITEV

Podatke smo dobili z merjenjem dolžine cevi, pri kateri se pojavi resonanca za določeno znano frekvenco, ki smo jo generirali s pomočjo računalnika. Pri naši umeritvi torej frekvenca predstavlja neodvisno, dolžina cevi pa odvisno spremenljivko.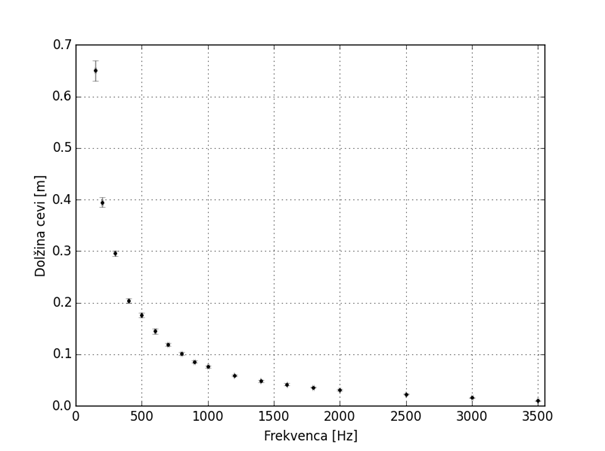

Slika 1: Prikaz meritev z upoštevanimi merskimi napakami (večja slika)

 

Iz same teorije za lastne frekvence sledi enačba za prvo lastno frekvenco (c-hitrost zvoka,d-dolžina cevi, ν- frekvenca):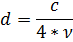


Ker pa se osnovna enačba ne ujema dobro z meritvami, kar je jasno razvidno tudi iz slike 2, jo je potrebno prilagoditi s parametroma A in B: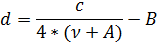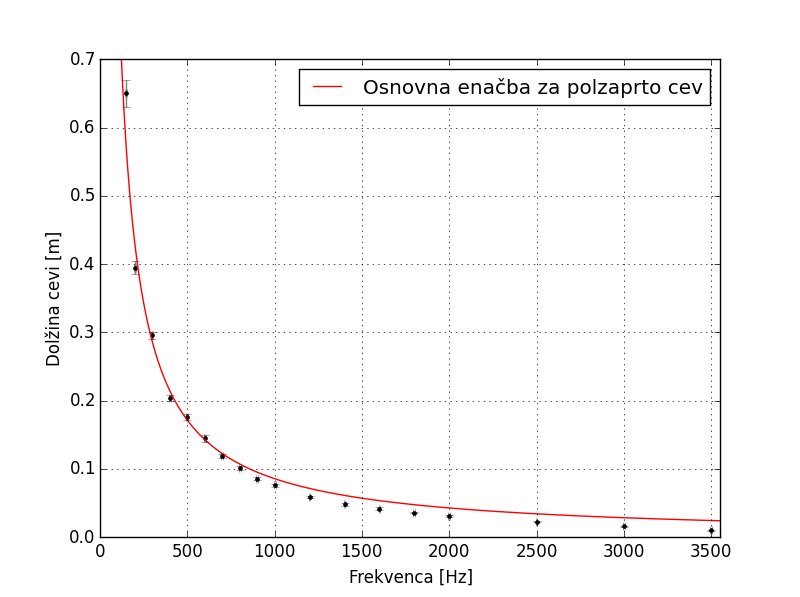



Slika 2: Neujemanje osnovne enačbe za polodprto cev z našimi podatki (večja slika)


Ujemanje prirejene funkcije je zelo blizu podatkov, kar je tudi razvidno na sliki 3. Vrednosti pri večini meritev padejo v okvir napake samih meritev, za ostale pa je potrebno upoštevati še sprejemljiv razpon pri novih parametrih.


Tabela 1: Vrednosti parametrov z absolutnimi napakami

Za obdelavo podatkov smo uporabljali Python, predvsem knjižnice Scipy, Numpy in Matplotlib.

Slika 3: Ujemanje prilagojene enačbe z izmerjenimi podatki (večja slika)

S tem smo pridobili enačbo, ki povezujejo prvo lastno frekvenco in dolžino cevi a v tej obliki še ni koristna za naš končni namen, merjenje neznane frekvence s spreminjanjem dolžine cevi, zato moramo iz nje izpostavit frekvenco. Dobimo naslednjo enačbo:

Slika 4: Funkcija za določanje frekvence v odvisnosti od dolžine cevi. V ozadju prikazane meritve za grobo primerjavo. (večja slika)

Za določanje kvalitete ujemanja funkcije podatkom uporabljamo vrednostx^2, to je seštevek kvadratov odstopanja funkcije od podatkov v merjenih točkah. Robne točke so točke, kjer je napaka najbolj opazna bodisi zaradi samega odčitka pri visokih frekvencah bodisi zaradi razpotegnosti in težavnosti iskanja maksimuma pri nizkih frekvencah, temu se posvetimo tudi kasneje pri napakah. Izračunali smo še x^2 brez robnih umeritvenih točk, če bi bilo ujemanje vseh točk enako bi zaradi tega pričakovali približno 10% spremembe x^2 .


Tabela 2: Seštevek kvadratov odstopanja od funkcije z in brez robnih točk

Slika 5: Primerjava osnovne in prilagojene enačbe za polzaprto cev (večja slika)

Naša glavna enačba za določanje frekvenc je torej:

Za c se ob nepoznavanju realnih pogojev uporablja 343 [m/s], kar je tudi vrednost uporabljena pri izračunih parametrov

Za enostaven izračun uporabimo le relativno težo naše ocenjene napake meritve dolžine, ki vsebuje tako napako meritve dolžine kot tudi napako pri iskanju maksimuma.

Pri izračunu s pomočjo računalniškega programa, pa si lahko privoščimo tudi upoštevanje vseh nedoločenosti parametrov.

Enačba vrne smiselne rezultate glede na teorijo polzaprte cevi, saj se od nje razlikuje le za nek konstanten faktor, kar je razvidno tako iz enačbe kot tudi iz grafa. V teoriji je potrebno za upoštevanje valjaste geometrije potrebno dolžini prišteti še 0.3 premera (http://www.fonema.se/mouthcorr/mouthcorr.htm), s tem pa se prav tako lepo ujema naš izračunan faktor B.

Glavne predpostavke uporabljene pri izračunu parametrov, ki lahko pripeljejo tudi do nedoločenosti so konstantna frekvenca izvora pri umeritvi, hitrost zvoka in natančnost naših meritev ter le tem pripisanih napak. Na kvaliteto izvora težko vplivamo, druge dva pa bi s primerno opremo in dovolj časa lahko izboljšali. Hitrost zvoka bi lahko merili s primernimi napravami oz. spremljali pogoje od katerih je odvisna in jo izračunali. Kvaliteto meritev bi lahko izboljšali z večjim številom meritev in posledično manjšo slučajno napako.

Predpostavka glede hitrosti zvoka ima vpliv le na enačbo iz teorije polzaprte piščali, kar lahko uporabimo tudi za pojasnilo večje natančnosti enačbe izpeljene iz prilagojene korenske funkcije. Vpliv je seveda odvisen od odstopanja naše predpostavljene vrednosti od dejanskega stanja.

Kvaliteta meritev pa predstavlja večji problem za enačb. Še posebno problematične so robne meritve, pri njih je bila meritev najtežja obenem pa imajo velik vpliv na končni rezultat. Glavni komponenti napak pri meritvah izhajata iz slušnega iskanja maksimuma in meritve dolžine.

Meritev dolžine predstavljajo nenatančnosti v načrtu in izdelavi same cevi ter nenatančnost pri odčitanju rezultata. Absolutne vrednosti teh instrumentalnih napak so konstantne, njihova relativna teža pa se povečuje pri majših dolžinah cevi, torej višjih frekvencah.

Iz slušnega iskanja pa izhajajo naključne nedoločenosti, vendar je tudi velikost le teh odvisna od frekvence. Maksimume je lažje iskati pri višjih frekvencah, saj so ostreje izraženi, obenem pa je pri teh frekvencah človeško uho občutljivejše. Relativna teža napak zaradi slušnega iskanja se torej z višanjem frekvence manjša.

Inštrumentalne nedoločenosti so bolj opazne pri višjih frekvencah, naključne pa pri nizkih. Za izračun je preudarno napako zaradi merjenja in napako zaradi iskanja združiti v ocenjeno napako dolžine. Oceno dobimo iz seštevka polovice intervala po katerem se »sprehajamo« pri končnem, finem iskanju maksimuma in napake meritve. Ta ocenjena napaka je pri večini frekvenc tudi najšibkejši člen v enačbi, odstopanja bi se lahko pojavila le pri zelo nizkih frekvencah, kjer znajo napake parametrov postati pomembnejše.