V tabelah so zbrane vse oznake in njihove vrednosti, ki smo jih uporabljali pri računanju relativne vlage v zraku.
| Oznaka | Enota | Pomen | Vrednost |
|---|---|---|---|
| $h_i$ | $\rm J/kg$ | Izparilna toplota vode | $2.5 \cdot 10^6$ |
| $h_a$ | $ \rm J/kg$ | Izparilna toplota antifriza | $0.86 \cdot 10^6$ |
| $M_v$ | $\rm g/mol$ | Molska masa vode | $18$ |
| $M_a$ | $\rm g/mol$ | Molska masa antifriza | $62$ |
Tabela 1: Enote, pomen in vrednosti posameznih oznak, katerih vrednosti so odvisne od vrste tekočine.
| Oznaka | Enota | Pomen | Vrednost |
|---|---|---|---|
| $T_0$ | $\rm K$ | Temperatura trojne točke vode | $273$ |
| $T_m$ | $\rm K$ | Temperatura mokrega termometra | Izmerimo |
| $T_s$ | $\rm K$ | Temperatura suhega termometra | Izmerimo |
| $e_{s0}$ | $\rm hPa$ | Nasičen parni tlak vode pri $T_0$ | $6.11$ |
| $e_{sv} (T)$ | $\rm hPa$ | Nasičen parni tlak pri temperaturi $T$ za vodo | Izračunamo iz meritev |
| $e_{sa} (T)$ | $hPa$ | Nasičen parni tlak pri temperaturi $T$ za etilen glikol | Izračunamo iz meritev |
| $M_s$ | $\rm g/mol$ | Molska masa suhega zraka | $29$ |
| $R$ | $\rm J/mol K$ | Plinska konstanta | $8.3145$ |
| $p$ | $\rm hPa$ | Tlak | Izmerimo |
| $c_p$ | $\rm J/kgK$ | Specifična toplota zraka | $1004$ |
| $f$ | $\%$ | Relativna vlažnost zraka | Izmerimo in izračunamo |
Tabela 2: Enote, pomen in vrednost splošnih oznak
Vlažnost zraka nam pove vsebnost vodne pare v zraku.
Nasičen parni tlak vodne pare v zraku opisuje Claussius-Clapeyronova enačba:
$e_{sv}(T)=e_{s0} \cdot e^{\frac{h_i M_v}{R}(1/T_0-1/T)}$,
nasičen parni tlak etilen glikola pa enačba, ki jo navaja CHERIC:
$ln(e_{sa})=-25.99771\cdot ln(T)-\frac{14768.57}{T}+191.4250+2.062331\cdot 10^{-5}\cdot (T)^2$
Zanimala nas je relativna vlaga $f$, ki je razmerje med dejanskim parnim tlakom $e$ in nasičenim parnim tlakom $e_s$ pri določeni temperaturi zraka:
$f=\frac{e}{e_s} \ \ [\%]$
Psihrometer, ki se uporablja v meteoroloških postajah za merjenje vlage v zraku, je sestavljen iz dveh ločenih termometrov. En od termometrov (moker) ima bučko, ki je mokra, drugi (suhi) pa ima suho bučko. Mimo bučk termometrov teče stalen tok zraka. Slednje dosežemo s postavitvijo ventilatorja ob psihrometer. Suhi termometer kaže temperaturo zraka $T_s$. Mokri termometer kaže temperaturo vlažnega zraka $T_m$. $T_m$ odčitamo, takrat, kadar se temperatura mokrega termometra ustali in je vlaga v zraku v bučki mokrega termometra nasičena $e=e_s$ oz. je relativna vlaga $f$ v bučki mokrega termometra 100%.
Na splošno se meritev specifične vlage s psihrometrom uporablja kot standardni način za določanje vlage v zraku.
Slabost psihrometra je predvsem v tem, da je njegovo delovanje odvisno od temperature. Ob nizkih temperaturah (pod 0°C) krpice zmrznejo in naprava ne deluje več. Prav tako je za delovanje klasičnega psihrometra potrebna konstantna prisotnost merilca. Meritev je treba spremljati, da je krpica dovolj navlažena in gledati kdaj se temperatura ustali. Proces je prav tako dolgotrajen, ker da se temperatura ustali traja nekaj časa.
Temperatura mokrega termometra je nižja od temperature suhega termometra, saj voda ob bučki mokrega termometra izhlapeva in zato porablja energijo. Energijska bilanca za zrak v bučki mokrega termometra:
$mc_p \int_{T_m}^{T_s}\rm d T=-h_i \int_{m_0}^{m_v}dm_v$
$mc_p\Delta T=-h_i(m_v-m_0)$
$c_p\Delta T =-h_i(q_0-q_s)$
$\rm d q$ - sprememba specifične vlage zaradi izhlapevanja,
$q_0$ - specifična vlaga zraka,
$q_s$ - nasičena specifična vlaga,
$\rm d T = T_s - T_m$
Iz tega lahko izpeljemo:
$h_i \left[ q_s(T_m)-q(T_s)\right] = c_p \cdot (T_s - T_m)$
Od tod lahko z izmerjenima temperaturo mokrega termometra $T_m$ in temperaturo suhega termometra $T_s$ ter izračunano nasičeno specifično vlago $q_s(T_m)$ :
$q_s(T_m)=\frac{e_{sv}(T_m) \cdot M_v}{p \cdot M_s}$
pri čemer je:
$e_{sv}(T_m)=e_{s0} \cdot e^{\frac{h_i M_v}{R}\left(1/T_0-1/T_m\right)}$
dobimo specifično vlago zraka $q(T_s)$:
$q(T_s)=q_s(T_m)-\frac{c_p}{h_i}(T_s-T_m)$
Ker nas je zanimala relativna vlaga zraka $f$, smo morali izračunati parni tlak zraka $e$ pri temperaturi suhega $e(T_s)$ in mokrega termometra $e(T_m)$ iz specifične vlage zraka:
$q(T_s)=\frac{e(T_s)M_v}{pM_s}$ in
$q(T_m)=\frac{e(T_m)M_v}{pM_s}$.
Ko smo zadnji dve enačbi vstavili v zadnjo enačbo za izračun specifične vlage zraka , smo dobili značilno psihrometrično enačbo, ki nam poda vrednost parnega tlaka zraka pri temperaturi suhega termometra $e(T_s)$:
$e(T_s)=e_{sv}(T_m)-\frac{c_pM_s}{M_vh_i}p(T_s-T_m)$.
Na koncu izračunamo še relativno vlago $f$, ki smo jo v rezultatih uporabljali kot vlaga zraka:
$f=\frac{e_{sv}(T_m)}{e_{sv}(T_s)}-\frac{c_pM_s}{M_vh_i}p(T_s-T_m)\frac{1}{e_{sv}(T_s)}$.
pri čemer je:
$e_{sv}(T_s)=e_{s0} \cdot e^{\frac{h_iM_v}{R}\left(1/T_0-1/T_s\right)}$
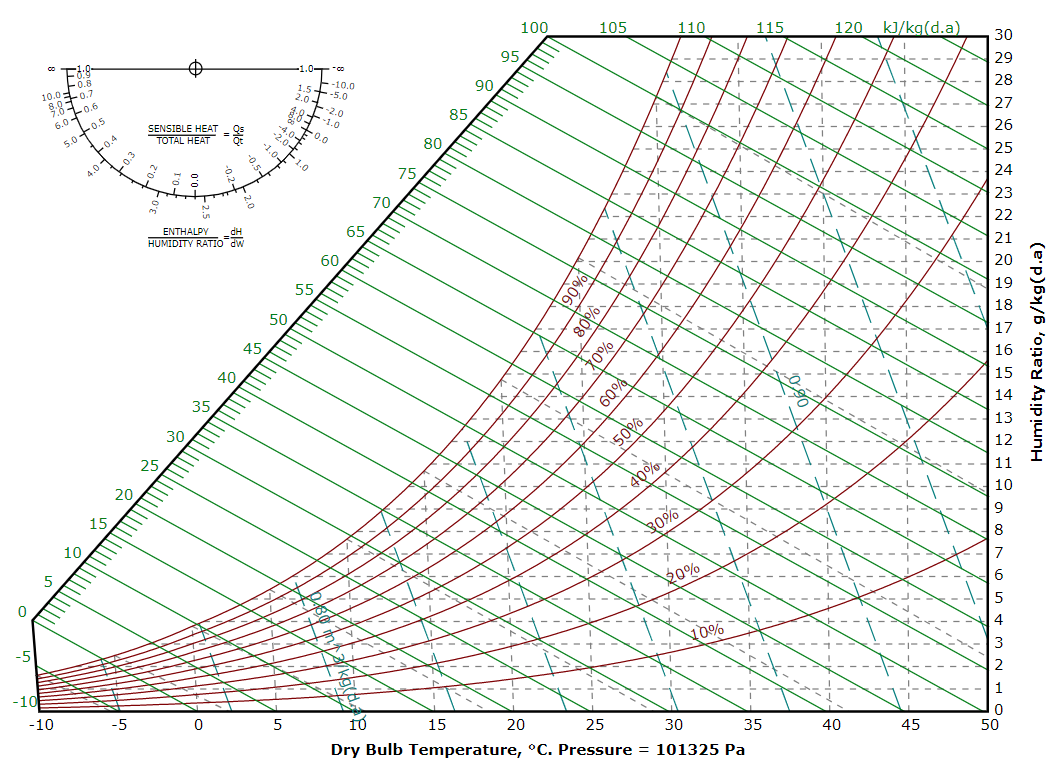Slika 3: Psihrometerski diagram
V primeru, ko smo krpico omočili v antifriz, smo prav tako upoštevali enačbo za energijsko bilanco za zrak v bučki mokrega termometra, vendar smo pri tem upoštevali, da iz mešanice vode in etilen glikola izhlapeva vsaka komponenta posebej:
$mc_p \int_{T_m}^{T_s}\rm d T=-h_i \int_{m_0}^{m_v}dm_v + h_a\int_0^{m_a}dm_a$
$mc_p\Delta T=-h_i(m_v-m_0)+h_am_a$
$c_p\Delta T =-h_i(q_0-q_s)+h_aq_a$
Sledeči postopek računanja je enak kot v primeru za vodo. Upoštevamo, da za vodo velja:
$q(T)=\frac{e_{sv}(T)M_v}{pM_s}$
in za etilen glikol:
$q(T)=\frac{e_{sa}(T)M_v}{pM_s}$
Parni tlak izračunamo po enačbi:
$e=e_{sv}(T_m)+\frac{h_aM_a}{h_iM_v}e_{sa}(T_m)-\frac{c_pp\Delta T}{h_i M_v}$
Da dobimo relativno vlažnost, moramo parni tlak deliti z nasičenim parnim tlakom $e_{sv}(T_s)$, ki smo ga računali po enačbi za vodo:
$e_{sv}(T_s)=e_{s0}\cdot e^{\frac{h_iM_v}{R}(1/T_0-1/T_s)}$
Ugotovimo, da enačba za računanje relativne vlage:
$f=\frac{e_{sv}(T_m)}{e_{sv}(T_m)}+\frac{h_aM_a}{h_iM_v}\frac{e_{sa}(T_m)}{e_{sv}(T_s)}-\frac{c_pp\Delta T}{h_i M_v e_{sv}(T_s)}$
ni odvisna od razmerja vode in etilen glikola v mešanici antifriza. Pri izpeljavi smo upoštevali, da se v mešanici voda-antifriz izparilni toploti $h_i$ in $h_a$ ne spremenita.