KONVEKCIJA
Konvekcija je gibanje molekul v plinu in je eden glavnih načinov prenosa toplote in prenosa snovi.
Sveča segreva zrak v svoji oklici, kar pomeni, da molekulam dovaja energijo in se le-te hitreje gibljejo. Zaradi tega zasedajo večjo prostornino oz. rečemo, da je zrak redkejši.
Redkejši topel zrak se dvigne nad gostejšega hladnega.
Kot približek vzamemo idealen plin. Tlak P, prostornino V, količino plina N in temperaturo T lahko povežemo z enačbo idealnega plina
P*V=N*R*T,
kjer je R idealna plinska konstanta (8,314 v enotah J/(mol*K)).
Recimo, da začnemo s količino zraka N pri tlaku P, prostornini V1 in temperaturi T1 in ga segrejete na temperaturo T2. Enačbo idealnega plina lahko prepišemo kot
P*V1/(N*T1) =R=P*V2/(N*T2),
ki jo je z malo algebre mogoče rešiti:
V2=V1*T2/T1.
Iz tega vidimo, da če segrejete plin tako, da T2>T1, dobiš V2>V1 kar pomeni, da se plin širi. Ker imate enako količino plina, se masa ne spremeni, tako da je gostota pred segrevanjem
enaka ρ1=m/V1 in gostota po segrevanju je ρ2=m/V2.
Zdaj je sila teže na vroč zrak (Fg) podana z maso vročega zraka, pomnoženo z gravitacijsko konstanto g (9,8 m/s2)
Fg= ρ2*V2*g.
Tukaj je masa vročega zraka podana z gostoto vročega zraka ρ2, pomnoženim s prostornino vročega zraka V2. Vzgojna sila na balon je podana z maso premaknjenega zraka, pomnoženo z gravitacijsko konstanto:
Fb= ρ1*V2*g.
Tukaj je masa zračnega izpodrivanja podana z gostoto okoliškega hladnega zraka ρ1, pomnoženo s prostornino vročega zraka V2. Zdaj je vzgonska sila navzgor in gravitacijska sila navzdol, tako da je neto sila podana z
F=Fb - Fg= ρ1*V2*g - ρ2*V2*g=m*g* (V2/V1- V2/V2),
Kar je mogoče prepisati z uporabo razmerja iz zakona idealnega plina (V2=V1*T2/T 1), da dobimo:
F=m*g*(T2/T1-1).
Ta enačba kaže, da ko segrevate zrak T2>T1 (tj. T2/T1>1), dobite pozitivno silo (F>0), kar pomeni, da je sila navzgor in se zrak dvigne, tako pa ob stiku potiska spodnjo stran spirale, ki se zaradi naklona prične vrteti.
Vroč zrak, ki se dvigne, nadomesti hladen zrak, ki se segreje in zato dvigne. Tak tok zraka se imenuje konvekcijski tok.
OPOZORILO: MODEL VRTENJA ŠE NI PREGLEDAN
MODEL VRTENJA SPIRALE
1. RADIJ
1.1 Radij spirale
Radij Arhimedove spirale se s središčnim kotom spreminja po naslednji formuli:

w predstavlja znano maksimalno razdaljo med zaporednima ovojema spirale.
1.2 Razdalja od razpolovišča traku do središča
Za računanje navora smo aproksimirali, da je težišče vsakega dela traku točno na njegovem razpolovišču. Zato smo potrebovali še odvisnost le-tega
od središčnega kota:
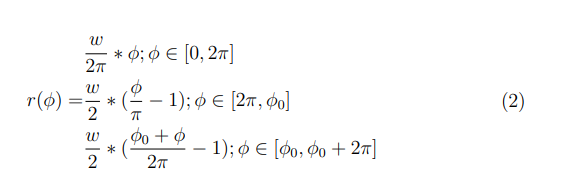
2. KOT GLEDE NA VODORAVNICO
Za izračun navora sil bomo potrebovali kot ki ga oklepa vsak delček spirale z vodoravnico - θ. Za določitev tega kota bomo potrebovali spremembo višine v odvisnosti od središčnega kota: z(ϕ).
Iz analize podobnih problemov sklepamo, da je ta odvisnost povezana s hiperboličnimi kotnimi funkcijami: z(ϕ) = sinh(ϕ/A). Postavili smo nekaj različnih kačic na palico in izmerilivišine
različnih delov. Dobljenim meritvam smo z GNUplotom fitali zgornjo funkcijo ter dobili naslednje vrednosti parametra A:
.png)
Predvidevamo tudi, da je parameter A linearno odvisen od razmerja mase in širine traku, zato lahko poiščemo premico, ki se najboljše prilagaja podatkom iz zgornje tabele:
.png)
Dobili smo koeficient premice: k = −81000(1 ± 0, 24) m/kg in začetno vrednost n = 2400(1 ± 0, 20)
Za računanje bomo potrebovali θ(ϕ). Do tega lahko pridemo tako:
.png)
3. NAVOR ZRAČNEGA UPORA
3.1 Reynoldsovo število
Za izračun upora moramo najprej ugotoviti, če je tok zraka okoli vrteče se spirale laminaren ali turbolenten. Pri tem si bomo pomagali tako, da bomo aproksimirali vrednost Reynoldsovega števila:
.png)
Pomen količin uporabljenih v enačbi:
- ρ - gostota zraka, uporabili smo vrednost pri sobni temperaturi
- v - hitrost toka glede na telo, uporabili smo
zvezo v = ωr,kjer smo za r vzeli največjo vrednost(radij spirale)
L - značilna linearna razsežnost, to količino
smo ocenili s premerom spirale
- µ - dinamična viskoznost zraka, odvisna od temperature, nekje
med 2 ∗ 10^(−5) kg/ms in 2, 5 ∗ 10^(−5) kg/ms[1]
Glede na to, da smo za oceno uporabili najvišje možne vrednosti in da je Reynoldsovo število za naš poskus 3000, lahko sklepamo da je tok zraka okrog spirale delno nestabilen ali pa laminaren, vendar bomo
vseeno poskusili oceniti silo upora z linearnim zakonom upora.[2].
3.2 Linearni zakon upora
Sila upora na togo telo se aproksimira z linearnim zakonom upora:
.png)
Količine imajo enak pomen kot v odstavku 3.1, k pa je koeficient, ki je odvisen od oblike telesa. Tega za spiralo nismo znali določiti in najverjetneje ga tudi ni možno analitično.
Zato smo uporabili Stokesov zakon za silo na kroglo v tekočini(F = 6πrv)in spet določili L = 2r. Hitrost delov spirale se spreminja linearno s radijem v = ωr, zato lahko za
izračun sile uporabimo kar povprečno hitrost dela spirale:
.png)
3.3 Navor zračnega upora
Viskozna sila deluje vzporedno na vse dele rotirajoče spirale. Navor na spiralo pa da le vodoravna komponenta te sile. Ta komponenta ima vrednost F = Fu ∗ cosθ
.png)
Če bi želeli izračunati skupen navor sile upora bi morali poznati silo na vsak delček spirale ter vsak kot θ, ki ga ta del oklepa z vodoravnico. To silo v delu 3.2 ocenimo za celotno telo, zato nam ne preostane drugo
kot pa da naredimo približek, v tem primeru bomo zanemarili spreminjanje kota θ in uporabili povprečno vrednost le tega:
.png)
Končen navor zračnega upora:
.png)
4. SILA GOREČE SVEČE
Za aproksimacijo sile sveče smo uporabili naslednjo izpeljavo za pospešek zraka:
.png)
Nato smo izmerili polmer plamena sveče saj bomo za naš model potrebovali volumen vročega zraka, ki ga bomo aproksimirali z valjem, ki sega od plamena do dela spirale.
Izmerili smo rp = 2, 5mm ± 0, 025 mm.
Del sile, ki deluje na spiralo lahko torej zapišemo kot:
.png)
Opazimo, da za enačbo potrebujemo odvisnost temperature zraka nad svečo v odvisnosti od razdalje do plamena ter gostoto zraka, ki je pa odvisna od temperature, zato jo s pomočjo plinske
enačbe zapišemo v tej odvisnosti:
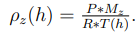
To odvisnost zdaj še vstavimo v enačbo sile:
.png)
4.1 temperatura v odvisnosti od višine
Odvisnost temperature zraka od višine smo določili eksperimentalno. Z IR termometrom smo merili temperaturo črnega papirja na različnih višinah nad svečo.
Meritve smo ponovili dvakrat ter uporabili večjo vrednost izmed izmerjenih kot temperaturo zraka na tej višini. Meritve smo zbrali v graf in ugotovili, da na merjenem
območju temperatura zraka pada razmeroma linearno:
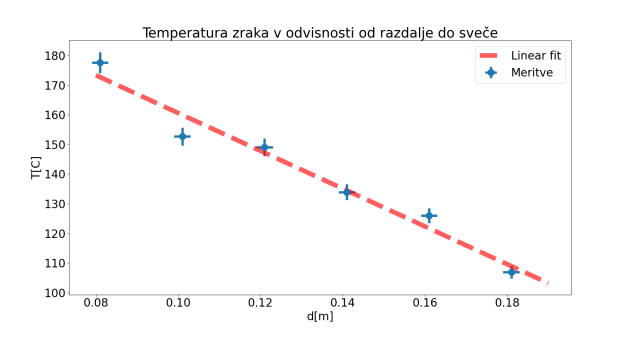
S programom GNUplot smo našli premico, ki se najbolje prilega našim meritvam, Ta premica ima enačbo:
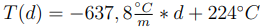
4.2 Končna sila
Če upoštevamo, da se temperatura spreminja linearno z višino potem lahko izračunamo silo sveče na katerikoli višini nad svečo:
.png)
.png)
4.3 Navor sile sveče
Pri poskusu smo uporabljali štiri sveče. Navor, ki ga sila curka dodaja spirali lahko izračunamo po osnovni formuli za izračun navora:
.png)
Navor lahko izračunamo, če poznamo razdaljo točke na spirali do sveče in pa središčni kot te točke. Razdaljo do sveče smo pri poskusih spreminjali in je torej znana vrednost, tudi središčni kot poznamo.
Paziti pa moramo, da smo imeli 4 sveče, zato izračunamo skupni navor vseh štirih sveč ΣM.
5. TEST MODELA
Na točki ko je navor upora zraka enak navoru, ki ga dodajajo sveče, bi se morala spirala vrteti z maksimalno hitrostjo. To hitrost lahko izračunamo z našim modelom, če poznamo podatke o spirali.
Tako lahko preverimo natančnost našega modela.
Poskusili bomo predvideti maksimalno hitrost za kačico z dvema zavojema ter polmerom 4cm. Računali bomo tudi tako, da je kačica na 12cm visokem stojalu - torej je od plamena sveče oddaljena za 10cm.
.png)
6. VIRI
[1] Engineers Edge, 9. 5. 2022, dostopno na: https://www.engineersedge.com/physics/viscosity of air dynamic and kinematic 14483.htm
[2] Nuclear Power, 9. 5. 2022, dostopno na: https://www.nuclear-power.com/nuclear-engineering/fluiddynamics/reynolds-number/reynolds-number-for-laminar-flow/
.png)
.png)
.png)

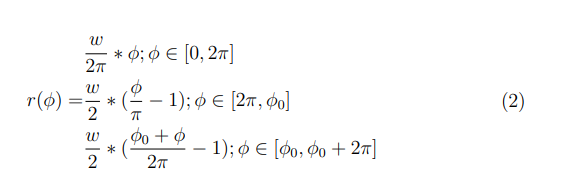
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
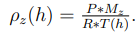
.png)

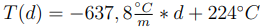
.png)
.png)
.png)
.png)