THE SPEED OF SOUND

Considering that the room was at a temperature of 15°C, the theoretical speed of sound is 340,00 m/s.

3.1 Resonance Tube

3.1.1 Measurements

Lenght of the tube: 1,05 m

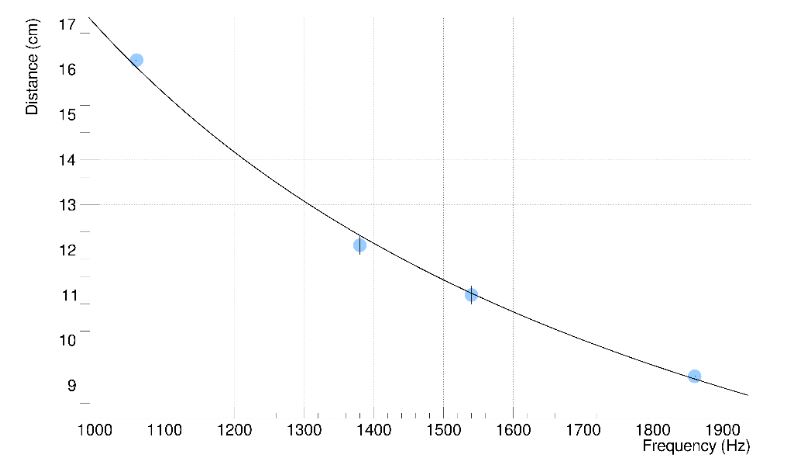
Frequency (Hz) Distance between nodes (cm)

Theoretical Experimental1 1st and 2nd2 2nd and 3rd3 Mean4

f₁₃ = 1052,4 1060,0 ± 0,8 16,0 ± 0,2 16,3 ± 0,3 16,2 ± 0,2

f₁₇ = 1376,2 1380,0 ± 0,8 12,5 ± 0,2 11,7 ± 0,3 12,1 ± 0,2

f₁₉ = 1538,1 1540,0 ± 0,8 11,1 ± 0,2 10,8 ± 0,3 11,0 ± 0,2

f₂₃ = 1861,9 1860,0 ± 0,8 9,5 ± 0,2 8,9 ± 0,3 9,2 ± 0,2

¹ The error used correspond to the sum of the uncertainty associated with choosing the correct resonant frequency (0,5 Hz since we could not choose to make steps smaller than 1 Hz) and the difference between the frequency chosen on the phone and detected by the computer (0,3 Hz)
² The error used correspond to the distance in which is not possible to perceive a change in the wave amplitude
³ The error is greater, since as one advance in the tube, the number of “undesirable” reflections increases, making it more difficult to find the precision position of the nodes
⁴ The error of the mean was obtained by calculating the propagation of errors (partial derivatives)

3.1.2 Calculations

The fitting function was deduced as follows:

$v = f λ = 2 f d \Leftrightarrow d = ν 2 f$

Where $ν$ is the speed of sound, $f$ is the frequency of the sound, 𝜆 is the wavelength of the sound and d is the distance between two consecutive nodes.

In order to maintain consistency between measurement units (distances measured in cm and speed obtained in m/s ), a factor of 100 was added.

+ $d (c m) = \frac{100}{2 f (H z)} v (\frac{m}{s}) = \frac{50}{f (H z)} v (\frac{m}{s})$

Fitting parameters Fitting function

$d (c m) = \frac{50}{f (H z)} v (\frac{m}{s})$ Velocity Experimental error Chi - Squared

340,01m/s 2,75m/s 1,98

Absolute error Relative error Experimental error¹

$e = | v - v_{t h e o r e t i c} |$ $e_{%} = \frac{| v - v_{t h e o r e t i c} |}{v_{t h e o r e t i c}} \cdot 100$ $δ v = u n c e r t a i n t y_{> %} \cdot v$

0,01m/s 2,94×10-3% 7,39m/s

¹ Since the experimental error obtained through the fitting function is smaller than the largest percentage uncertainty of the values used to make the calculation (weakest link rule), a new value was calculated according to it.
Velocity: [332,62; 347,40]m/s

3.2 Two Microphones

3.2.1 Measurements

Lenght of the tube: 1,01 m

Interval of time (ms)

Attempts¹ Mean²

3,057 ± 0,250 2,920 ± 0,115

2,920 ± 0,115

2,829 ± 0,204

3,014 ± 0,240

2,990 ± 0,230

2,920 ± 0,220

2,931 ± 0,226

2,947 ± 0,226

2,897 ± 0,210

2,986 ± 0,230

¹ The error used correspond to the sum of half the width of the initial peaks used to calculate the interval of time
² The error of the mean was obtained by calculating the standard deviation

3.2.2 Calculations

Velocity Experimental error¹ Absolute error Relative error

$v = \frac{d}{t}$ $δ v = \sqrt{| - \frac{d}{t^{2}} |^{2} (δ t)^{2}}$ $e = | v - v_{t h e o r e t i c} |$ $e_{%} = \frac{| v - v_{t h e o r e t i c} |}{v_{t h e o r e t i c}} \cdot 100$

345,89 m/s 13,62 m/s 5,89 m/s 1,73%

Velocity: [332,27; 359,51]m/s

3.3 Echo

3.3.1 Measurements

Lenght of the tube: 2,03 m

Interval of time (ms)

1st and 2nd¹ 2nd and 3rd¹ Mean²

11,800 ± 0,226 11,820 ± 0,228 11,875 ± 0,108

11,771 ± 0,226 11,721 ± 0,224

11,914 ± 0,230 11,915 ± 0,230

12,029 ± 0,240 12,030 ± 0,250

¹ The error used correspond to the sum of half the width of the initial peaks used to calculate the interval of time
² The error of the mean was obtained by calculating the standard deviation

3.3.2 Calculations

Velocity: [338,78; 345,00]m/s

Velocity Experimental error¹ Absolute error Relative error

$v = \frac{d}{t}$ $δ v = \sqrt{| - \frac{d}{t^{2}} |^{2} (δ t)^{2}}$ $e = | v - v_{t h e o r e t i c} |$ $e_{%} = \frac{| v - v_{t h e o r e t i c} |}{v_{t h e o r e t i c}} \cdot 100$

341,89 m/s 3,11 m/s 1,89 m/s 0,556%

¹ The error of the final result only takes into account time error because its relative uncertainty is bigger than relative uncertainty of measuring the distance (weakest link rule)

Frequency (Hz)		Distance between nodes (cm)
Theoretical	Experimental1	1st and 2nd2	2nd and 3rd3	Mean4
f₁₃ = 1052,4	1060,0 ± 0,8	16,0 ± 0,2	16,3 ± 0,3	16,2 ± 0,2
f₁₇ = 1376,2	1380,0 ± 0,8	12,5 ± 0,2	11,7 ± 0,3	12,1 ± 0,2
f₁₉ = 1538,1	1540,0 ± 0,8	11,1 ± 0,2	10,8 ± 0,3	11,0 ± 0,2
f₂₃ = 1861,9	1860,0 ± 0,8	9,5 ± 0,2	8,9 ± 0,3	9,2 ± 0,2

Fitting parameters	Fitting function
$d (c m) = \frac{50}{f (H z)} v (\frac{m}{s})$	Velocity	Experimental error	Chi - Squared
$d (c m) = \frac{50}{f (H z)} v (\frac{m}{s})$	340,01m/s	2,75m/s	1,98
Absolute error	Relative error	Experimental error¹
$e = \| v - v_{t h e o r e t i c} \|$	$e_{%} = \frac{\| v - v_{t h e o r e t i c} \|}{v_{t h e o r e t i c}} \cdot 100$	$δ v = u n c e r t a i n t y_{> %} \cdot v$
0,01m/s	2,94×10-3%	7,39m/s

Interval of time (ms)
Attempts¹	Mean²
3,057 ± 0,250	2,920 ± 0,115
2,920 ± 0,115
2,829 ± 0,204
3,014 ± 0,240
2,990 ± 0,230
2,920 ± 0,220
2,931 ± 0,226
2,947 ± 0,226
2,897 ± 0,210
2,986 ± 0,230

Velocity	Experimental error¹	Absolute error	Relative error
$v = \frac{d}{t}$	$δ v = \sqrt{\| - \frac{d}{t^{2}} \|^{2} (δ t)^{2}}$	$e = \| v - v_{t h e o r e t i c} \|$	$e_{%} = \frac{\| v - v_{t h e o r e t i c} \|}{v_{t h e o r e t i c}} \cdot 100$
345,89 m/s	13,62 m/s	5,89 m/s	1,73%

Interval of time (ms)
1st and 2nd¹	2nd and 3rd¹	Mean²
11,800 ± 0,226	11,820 ± 0,228	11,875 ± 0,108
11,771 ± 0,226	11,721 ± 0,224
11,914 ± 0,230	11,915 ± 0,230
12,029 ± 0,240	12,030 ± 0,250