THE SPEED OF SOUND

THEORETICAL INTRODUCTION

1.0 Speed of Sound in Everyday Life

In everyday life, knowledge of the speed of sound in air and how it propagates is implicit in different objects and basic ideas:

There is a time-difference of less than a millisecond between sounds reaching our left and right ear depending from where the sound comes;

In wind instruments, the speed of sound and the length of the pipe determines the pitch of the sound;

Supersonic airplanes (flying faster than the speed of sound) can break the sound barrier, thus the sound source will pass by a stationary observer before the observer actually hears the sound it creates.

1.1 Sound

Sound travels as a longitudinal wave (particles move parallel to the direction in which the wave is travelling) through a medium (does not exist in the vacuum) with a certain speed.
In the study of sound, two important properties must be considered: a sound wave consist of alternating compressions (high pressure) and rarefactions (low pressure) and the individual particles of the medium do not travel with the wave, but only vibrate back and forth centred on its equilibrium position.
Therefore the speed of sound in a medium depends on how quickly vibrational energy is transferred. In general, the equation for the speed of a mechanical wave (what the sound is) in a medium is expressed as:

$ν= \sqrt{\frac{elastic p r o p e r t y}{inertial p r o p e r t y}}$

v=elastic propertyinertial property . In an ideal gas the equation for the speed of sound is $v = \sqrt{\frac{γ R T}{M}}$ with $γ = 1, 4$ for air. As we can see the speed does not depend on the pressure at a constant temperature. To find the speed of sound in air, it’s possible to take different theoretical approaches to the problem. Thus, in this work, three different methods were used: resonance tube, two microphones and echo.

1.1 Resonance Tube

When a sound wave travels down a tube with one open and one close end, it can reflect, interfering with itself to produce a standing wave (combination of two waves moving in opposite directions, each having the same amplitude and frequency).
The standing wave pattern is characterised by points in the tube where the displacement of the air molecules is always zero (called nodes) and points where the displacement is at a maximum (called antinodes). Because sound waves are longitudinal waves, the particle motion associated with a standing sound wave is directed along the length of the pipe. This can be best represented in an animation.

https://en.wikipedia.org/wiki/Standing_wave#/media/File:Standing.gif

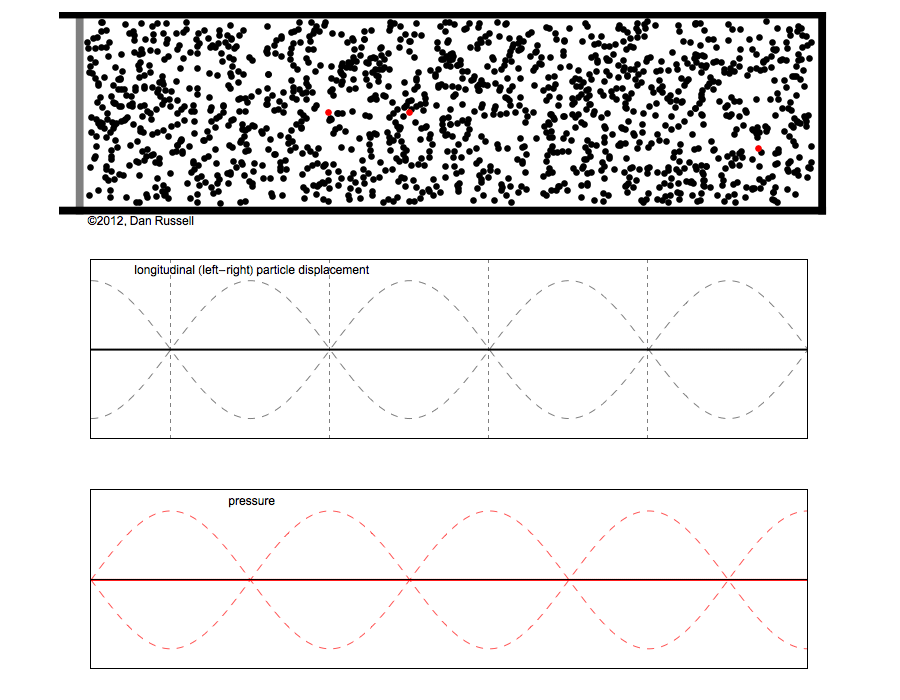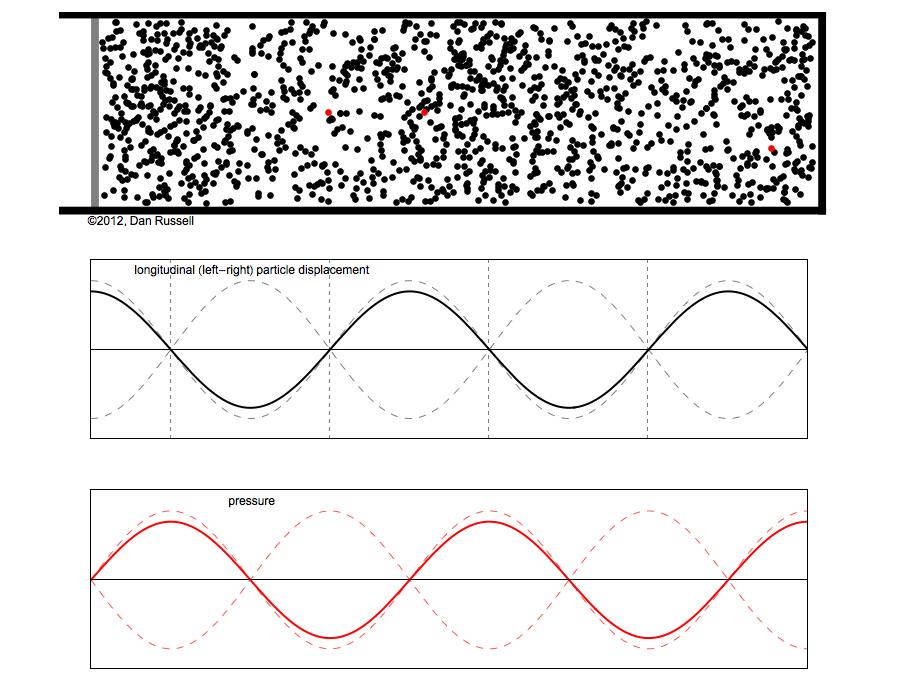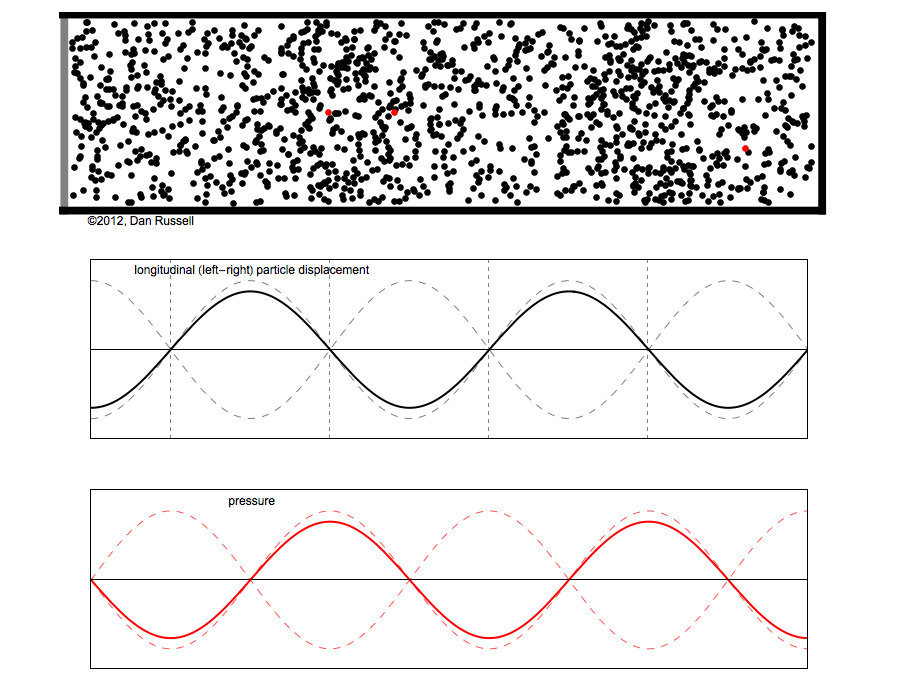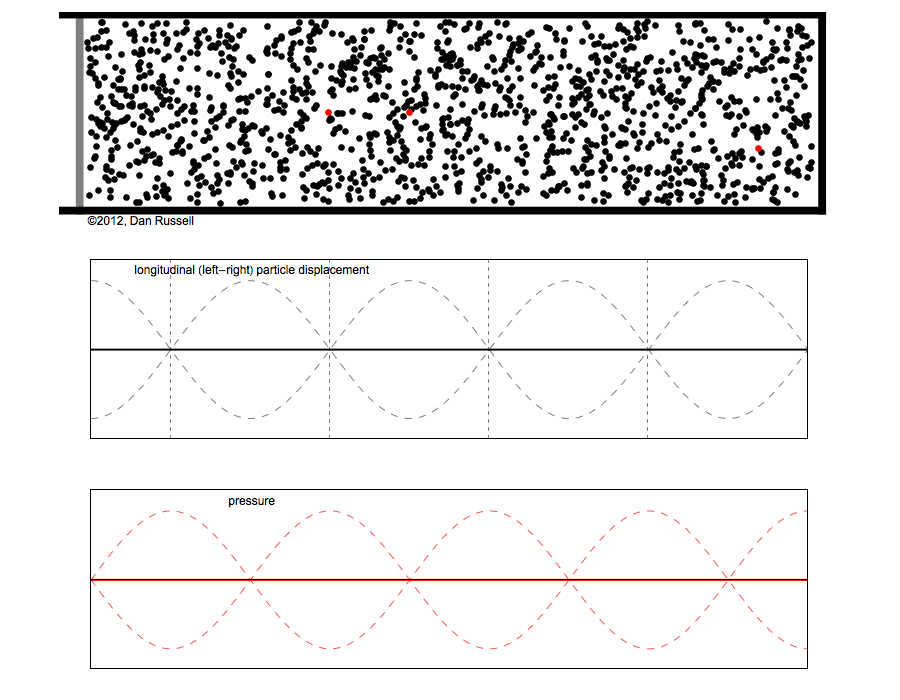
The leftmost red particle does not move at all, so it is located at a displacement node. The particles to the right and left of this stationary node first move toward the node, they become closer together and the local particle density increases (pressure compression). As the particles move away from the node the local particle density decreases (pressure rarefaction). Therefore, the pressure antinodes (regions where air pressure has the biggest variations) coincide with the displacement nodes. The second red particle moves with maximum displacement, so it is located at a displacement antinode. The local particle density in this region does not change as the particles move back and forth. The pressure nodes (regions where there are no air pressure variations) coincide with the displacement antinodes.

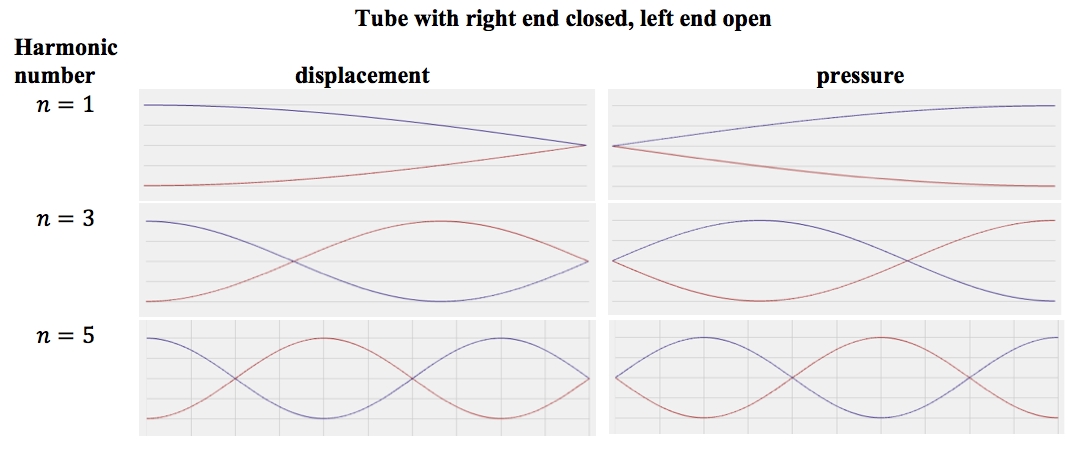https://www.compadre.org/osp/EJSS/4492/277.htm

In a tube with one open and one close end, the closed end acts as a displacement node because the air molecules cannot move beyond the rigid end and the open end acts as a displacement antinode since the air can move freely.

To achieve this pattern, it is necessary to use a particular frequency, called harmonic frequency, which can be found, using:

$> f_{n} = \frac{n \cdot ν}{4 l}$

Where $f_{n}$ is the harmonic frequency, n is an odd integer, v is the speed of sound and l is the length of the tube.
The factor 4 is used because the wave must travel the length of the tube twice and undergo a half-wavelength phase shift upon reflection at the closed end, and then travel the length of the tube again and undergo another half-wavelength phase shift upon exiting the open end. The positions of the nodes inside the tube correspond to:

$x_m = m \nu 4f x_{n} = ν \cdot n \cdot 4 f$

Where xm is the position of the node, m is an odd integer, v is the speed of sound and f is the harmonic frequency.

< Knowing both the distance between two consecutive nodes and the frequency, is possible to calculate speed of sound, using: $υ = 2 fd$

Where v is the speed of sound, f is the harmonic frequency and d is the distance between two consecutives nodes.
1.2 Two Microphones

If we consider two points collinear to the sound source, the sound will reach the closest point first and will arrive at the farthest with a delay, that is proportional to the distance between the two points. Knowing both the delay and the distance, is possible to calculate the speed of sound, using: $υ = \frac{d}{t}$

Where v is the speed of sound, d is the distance between the two points and t is the delay time.

1.3 Echo

An echo is a sound that is repeated because the emitted sound is reflected. It arrives at the source of the emitted sound with a delay, that is proportional to the distance between the source and the reflecting surface. Knowing both the delay and the distance, is possible to calculate the speed of sound, using: $υ = \frac{2 d}{t}$

Where v is the speed of sound, d is the distance between the source and the reflecting surface and t is the delay time. .