Teorija:

Kotaljenje po klancu lahko obravnavamo na dva načina. Prva možnost je neposredno z uporabo 2. N.z. in analizo sil in navorov, ki delujejo na kotaleče se telo. Druga možnost je z uporabo energijskega izreka.

Kotaljenje prazne pločevinke :

Opis gibanja s pomočjo navorov in sil :

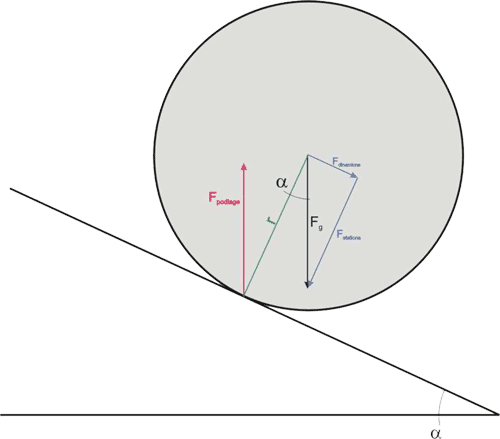Zapišemo enačbo za vsoto navorov za točko, kjer se pločevinka dotika podlage. Pomembno je tudi, da kasneje to upoštevamo pri izračunu ustreznega vztrajnostnega momenta. Vztrajnostni moment je potrebno izračunati za vrtenje pločevinke okoli točke za katero nastavimo enačbo navorov. Velja:

od tod dobimo:

Opis gibanja s pomočjo energijskega izreka :

Velja:

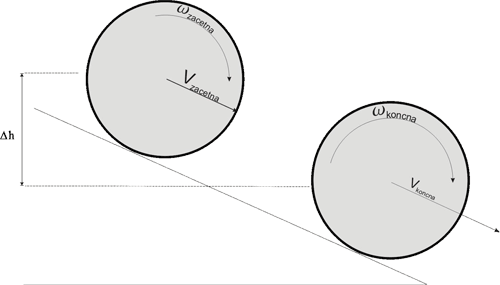
kjer je ΔW_pot (= Δh*m*g) sprememba potencialne enrgije , ΔW_kin (= m*(v²_končna - v²_začena)/2) sprememba kinetične enrgije, ΔW_rot (=j*(ω²_končna-ω²_začetna)/2) spremeba rotacijske energije.

Pri obravnavi gibanja smo privzeli, da se pločevinka po klancu samo kotali – se pravi da nič ne spodrsava in je zato zveza med ω in v enolično določena, zračni upor pa je zanemarljiv.

Kotaljenje polne pločevinke:

Za pločevinko, ki je povsem napolnjena s tekočino velja povsem enako kot za prazno pločevinko. Razlika je le v tem, da se spremeni vztrajnostni moment telesa, odvisno od tekočine s katero zapolnimo tekočino.

Kotaljenje pločevinke z ekscentrično utežjo:

Pri kotaljenju pločevinke pri kateri je bila vpeta utež ekscentrično je bolj nazorno, če gibanje obravnavamo z uporabo 2.N. zakona, saj je zanimivo opazovati tudi hitrost oz. pospešek kot funkcijo časa.

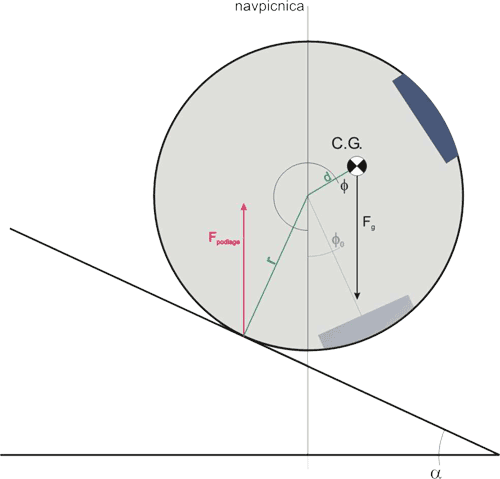
Nastavimo enako enačbo, kot pri opisu gibanja za prazno pločevinko z navori in silami.:

izkaže se, da diferencialna enačba ni analitično rešljiva.
Numeriča rešitev je podana tukaj (program za Mathematico).

Pločevinka delno napolnjena z viskozno tekočino:

Če pločevniko delno napolnimo z viskozno tekočino opazimo, da pločevinka relativno hitro doseže stacionarno stanje. Beri: po klancu navzdol se giblje premo enakomerno s konstantno hitrostjo. Razlaga z »mahanjem rok« je dokaj enostavna:

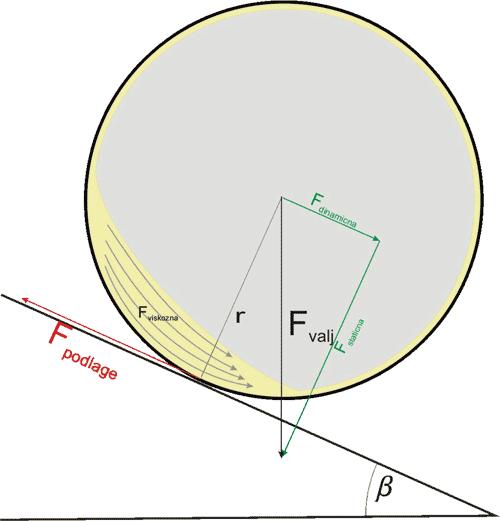
V pločevinki se ustvari »kaplja«, ki drsi po steni pločevinke. Imamo opravka z »viskoznim« trenjem med kapljo in steno pločevinke. Viskozno trenje narašča skladno s hitrostjo zato pri neki hitrsoti izenači silo oz. navor, ki kotali pločevinko po klancu navzdol. Posledično se kotal pločevnika po klancu navzdol s konstantno hitrosjo.
Matematična obravnava problema je dokaj kompleksna in težavna.

Vztrajnostni moment valja:

Če povlečemo paralelo s premim gibanjem, potem vztrajnostni moment zavzema enako vlogo kot masa. Enako velja tudi za ostale količine. Namesto sile imamo opravka z navorom, namesto linearnega pospeška imamo opravka s kotnim pospeškom in namesto linearne hitrosti nastopa kotna hitrost.

Vztrajnostni moment določa masa telesa in njegova razporeditev mase okoli osi vrtenja. Tako je recimo vztrajnostni moment masne točke glede na izbrano os enak produktu njene mase s kvadratom razdalje točke od osi ( j = m*r²). Vztrajnostni moment celotnega telesa za vrtenje okoli težšča dobimo tako, da na izrazu za masno točko izvedemo integracijo po celotnem volumnu telesa. Vztrajnostni moment telesa glede na poljubno os vrtenja lahko izrčunamo, če poznamo vztrajnostni moment telesa glede na os, ki je paralelna prvotni osi in gre skozi težišče. Poznati moramo še razdaljo med osema. Vztrajnostni moment lahko nato izračunamo po Steinerjevem izreku:

pri čemer je j izkan vztrajnostni moment, j* vztrajnostni moment glede na pralelno os vrtenja, ki gre skozi težišče in d razdalja med osema.