Projektno delo - Fizika in glasba
Predstavitev rezultatov
Kot smo omenili v poglavju teorija, smo pri eksperimentu merili Fourierovo transformacijo vpadnega zvočnega valovanja, ki smo jo označili z F(ν). Podatke teh meritev smo v kasnejši obdelavi predstavili s štirimi različnimi metodami:
-Meritve integrirane po frekvencah
-Meritve integrirane po frekvencah in normirane z integralsko glasnostjo
-Meritve povprečene in normirane z integralsko glasnostjo
-Meritve povprečene in pomnožene z "A weighting" in logaritmirane
Meritve integrirane po frekvencah
Najprej smo meritve integrirali po frekvencah, pri čemer smo uporabili formulo:Integral I(ν) je sorazmeren glasnosti zvoka, torej večja kot je vrednost integrala, bolj glasen je bil zvok, kar nas pri primerjavi različnih materialov in oblik zanima. Pri tem pa je treba upoštevati, da zgoraj navedeno velja ob predpostavkah, da smo na struno vsakokrat enako močno zabrenkali in da smo delali v tišini. Ker smo brenkali ročno in nismo bili sami v sobi, tega cilja nismo mogli natančno doseči.
Primerjava materialov:
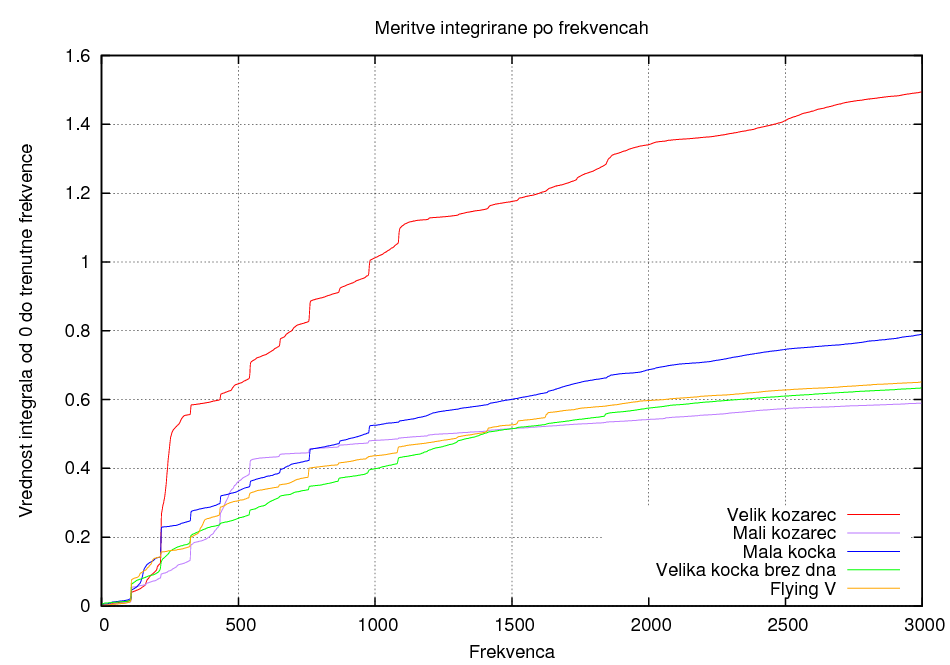
Razlika v polozaju luknje:
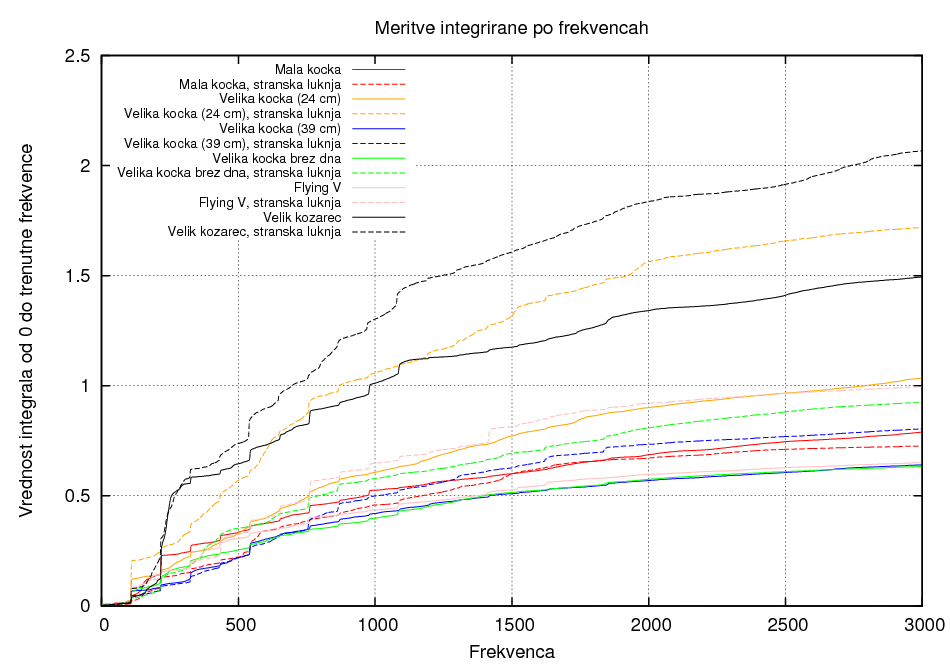
Razlika zaradi velikosti kocke:
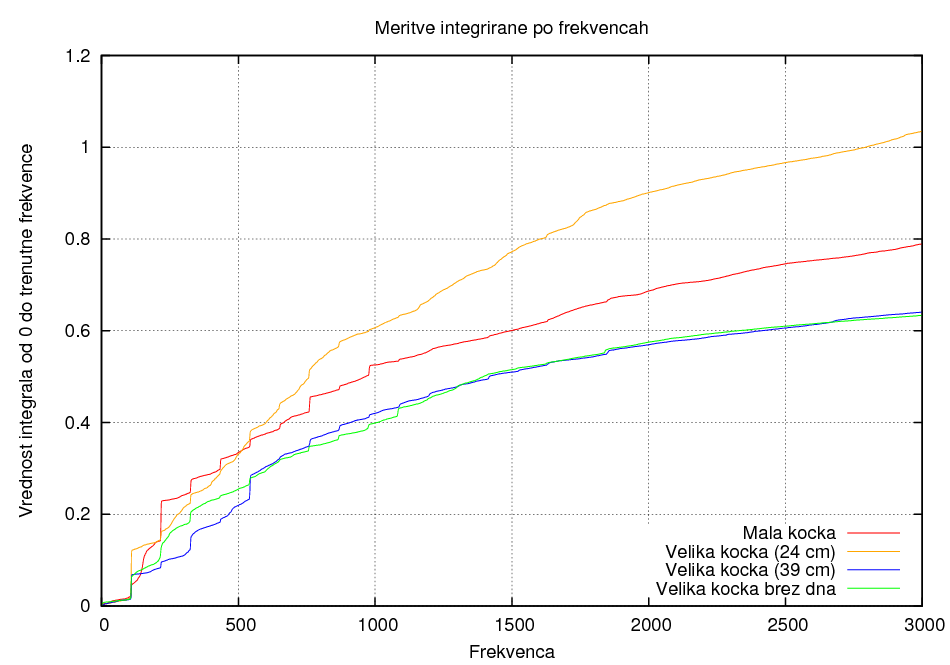
Iz rezultatov ni razvidno neke jasne tendence. Vidi se, da je najglasnejši velik kozarec, a je premalo ponovitev, da bi lahko iz tega naredili bolj natančno statistiko.
Meritve integrirane po frekvencah in normirane z integralsko glasnostjo
Ta metoda je nadaljevanje prve. Isti integral I(ν) smo integrirali s celotnim integralom Fourierove transformacije A, ki je: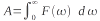
narisana količina na grafu je torej I(ν)/A.
Poudariti je potrebno tudi sledeče: ko gre ν -> ∞, gre količina I(ν)/A -> 1.
Sledeči grafi torej prikazujejo, katere frekvence so bolj zastopane pri katerih ohišjih. Frekvenca, pri kateri graf najbolj poskoči, je tista, ki je pri tem ohišju najbolj zastopana.
Primerjava materialov:
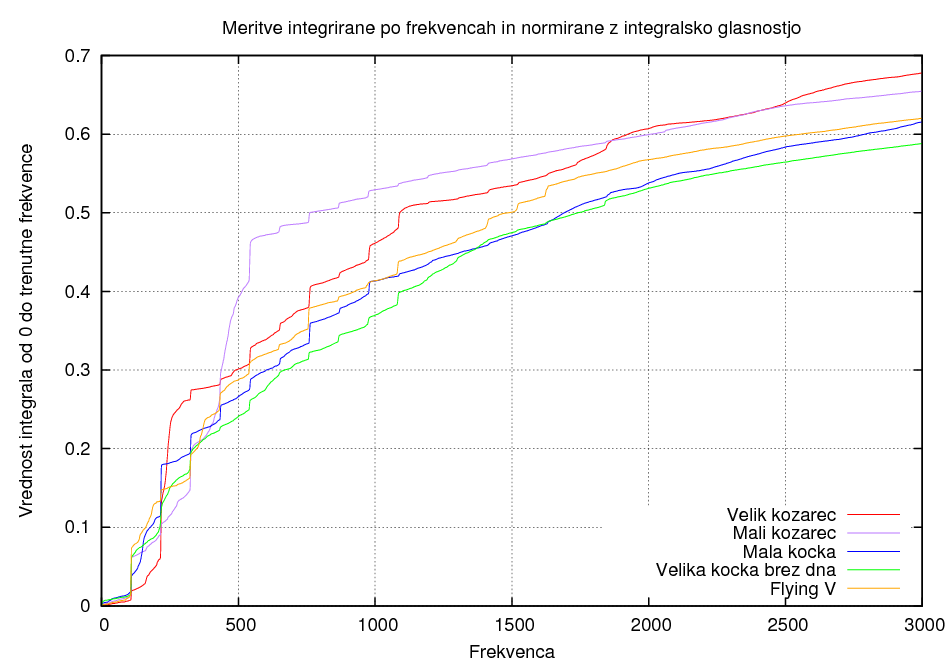
Razlika v polozaju luknje:
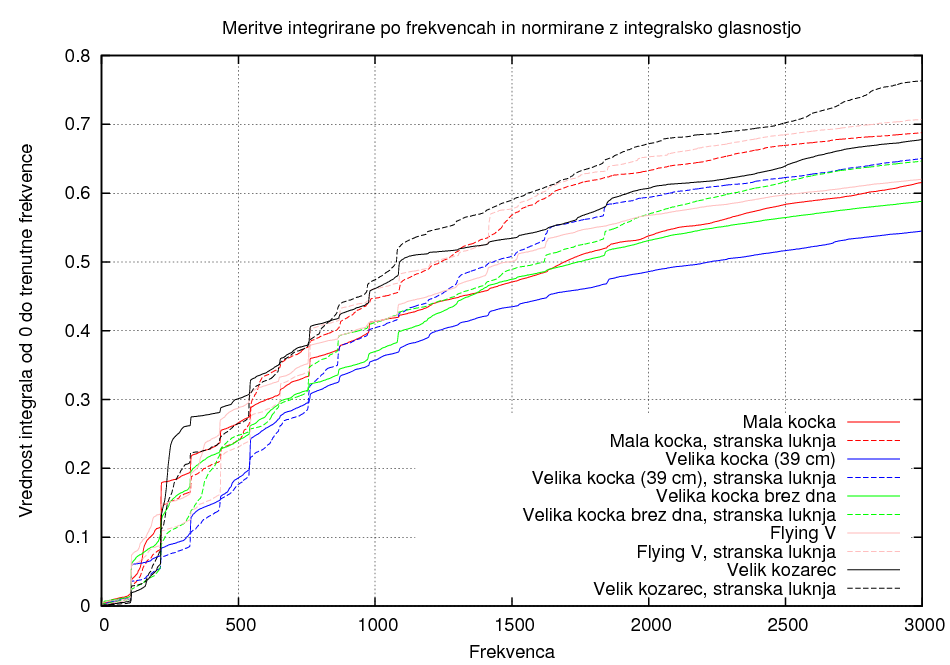
Razlika zaradi velikosti kocke:
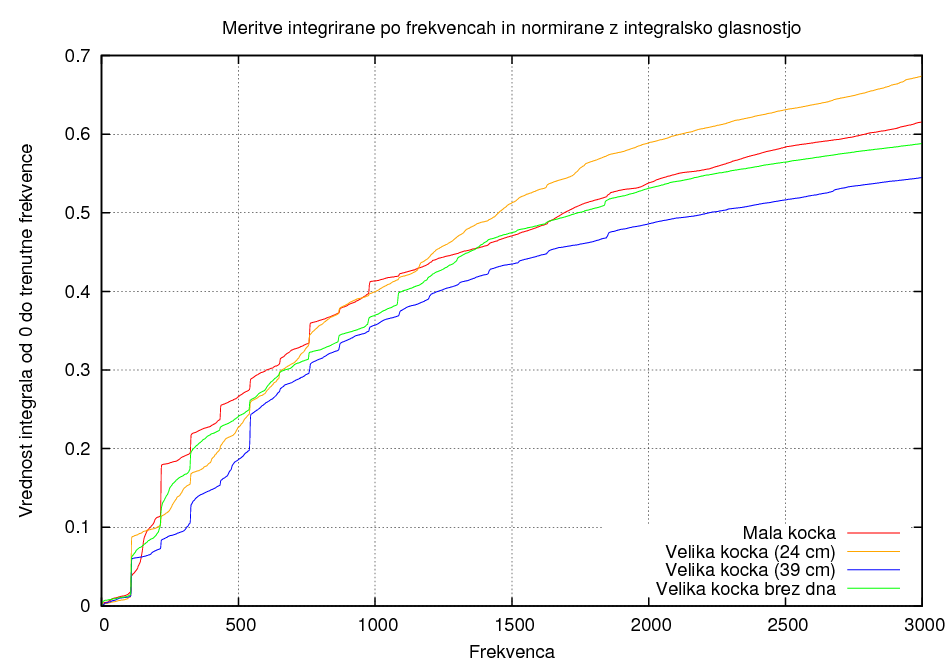
Iz zgornjih grafov je najbolj opazno, da so pri uporabi stranske luknje pri struni dosti bolj zastopane nižje frekvence.
Meritve povprečene in normirane z integralsko glasnostjo
Tokrat smo meritve povprečili in jih nato normirali z integralsko glasnostjo, pri čemer smo risali funkcijo F(ν)/A, ki ima vrhove pri točno določenih frekvencah. Osnovna frekvenca, na katero je bila uglašena struna, je 440Hz. Tudi iz tega grafa lahko vidimo, katera frekvenca je bolj zastopana, saj nam graf F(ν)/A pove isto kot I(ν)/A, vendar pa pri F(ν)/A gledamo le višino vrhov.Primerjava materialov 1:
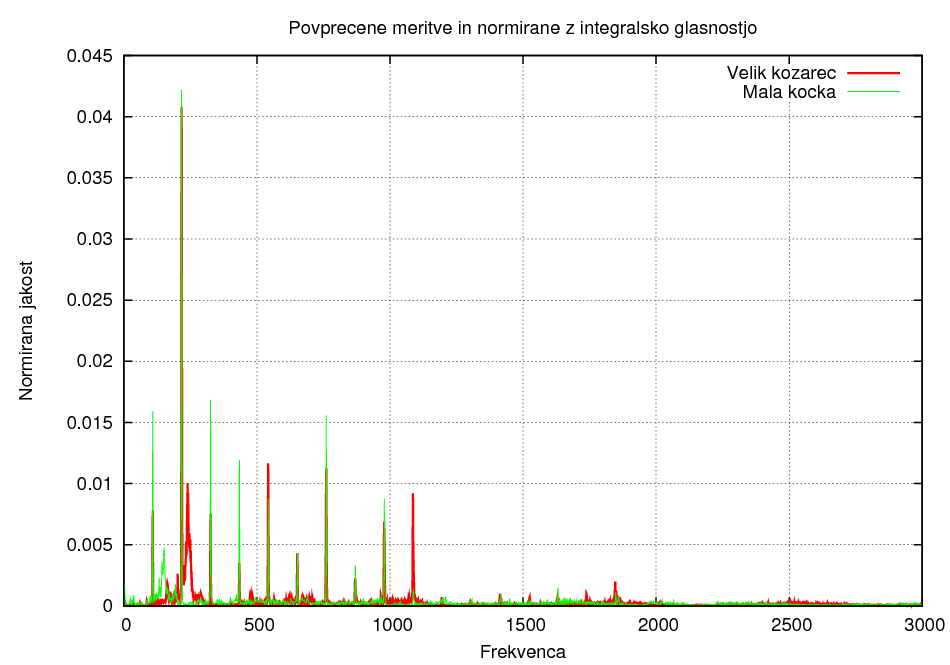
Primerjava materialov 2:
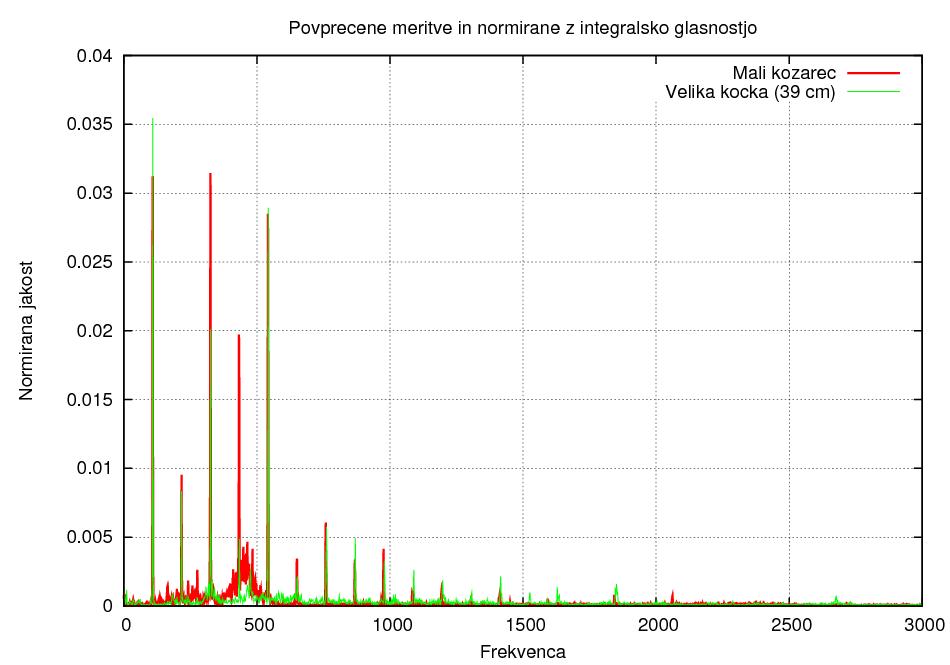
Primerjava oblik:
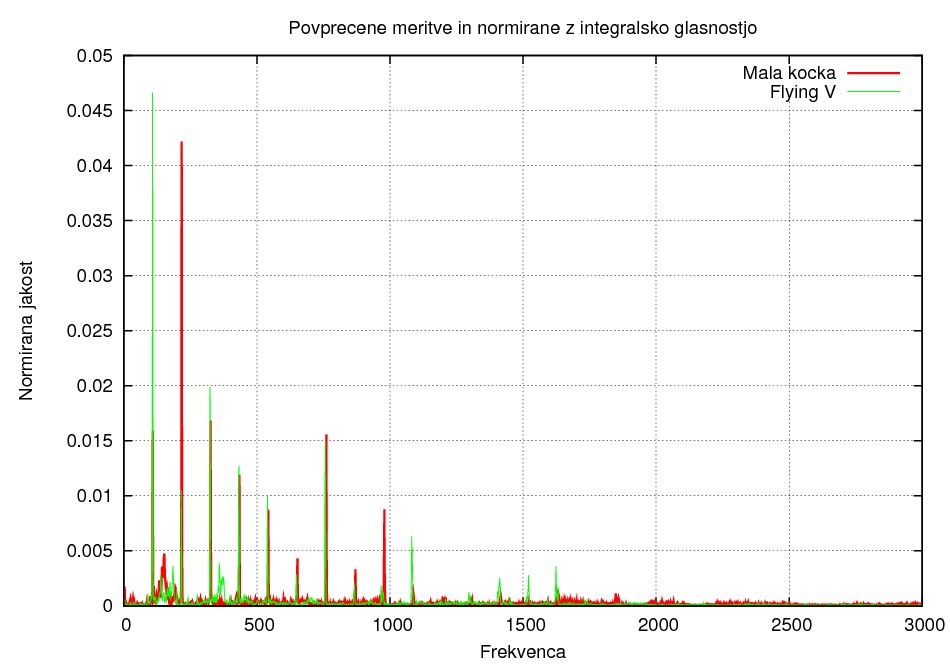
Razlika v polozaju luknje 1:
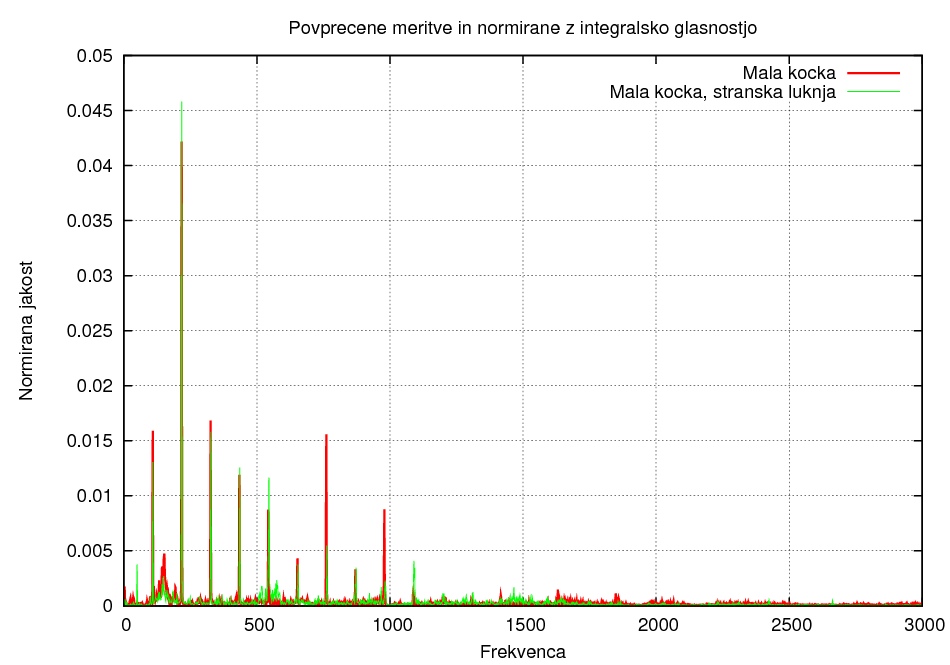
Razlika v polozaju luknje 2:
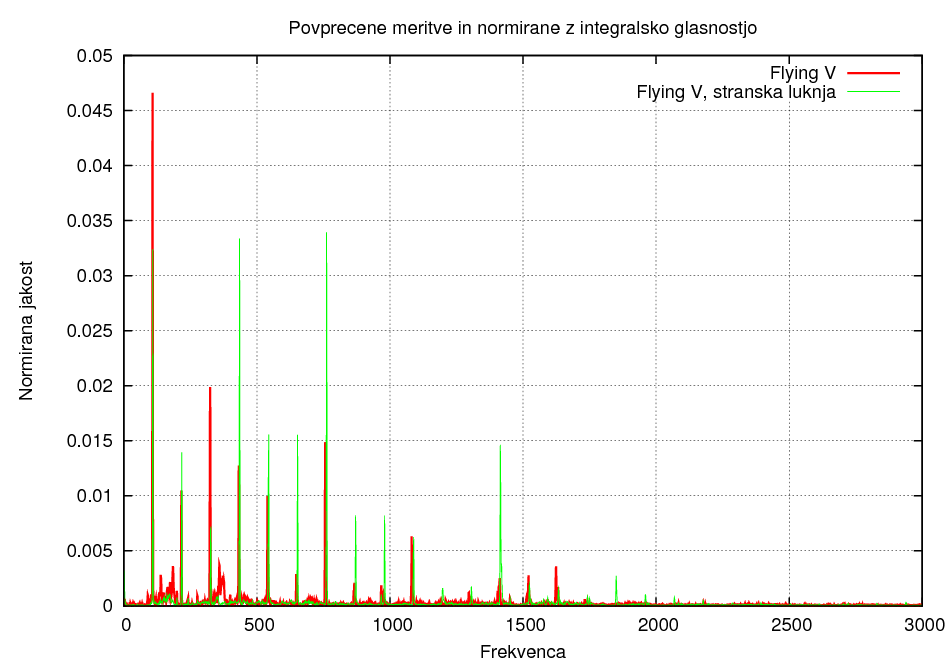
Razlika v polozaju luknje 3:
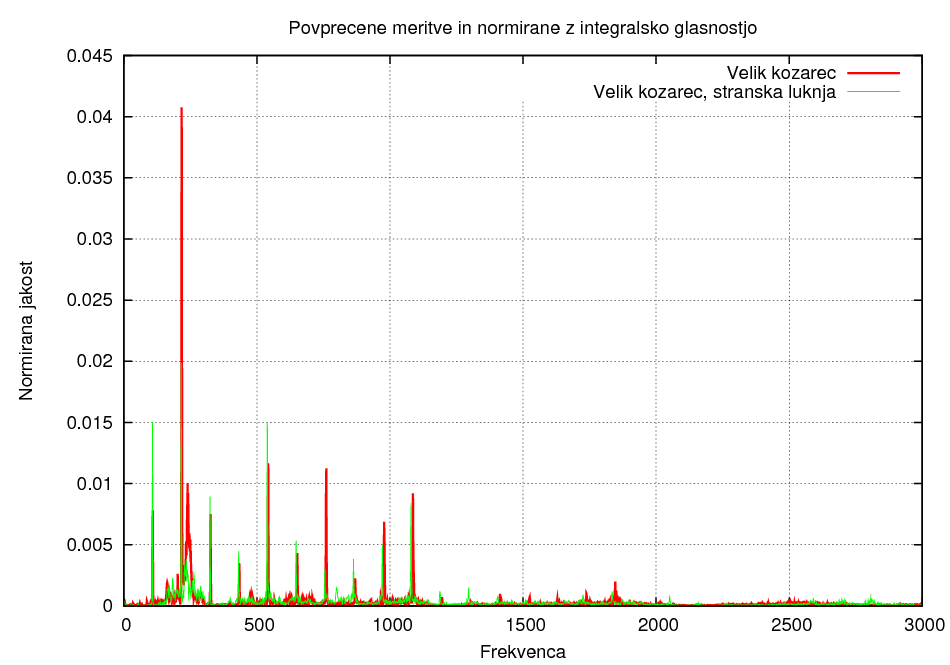
Razlika zaradi velikosti kocke:
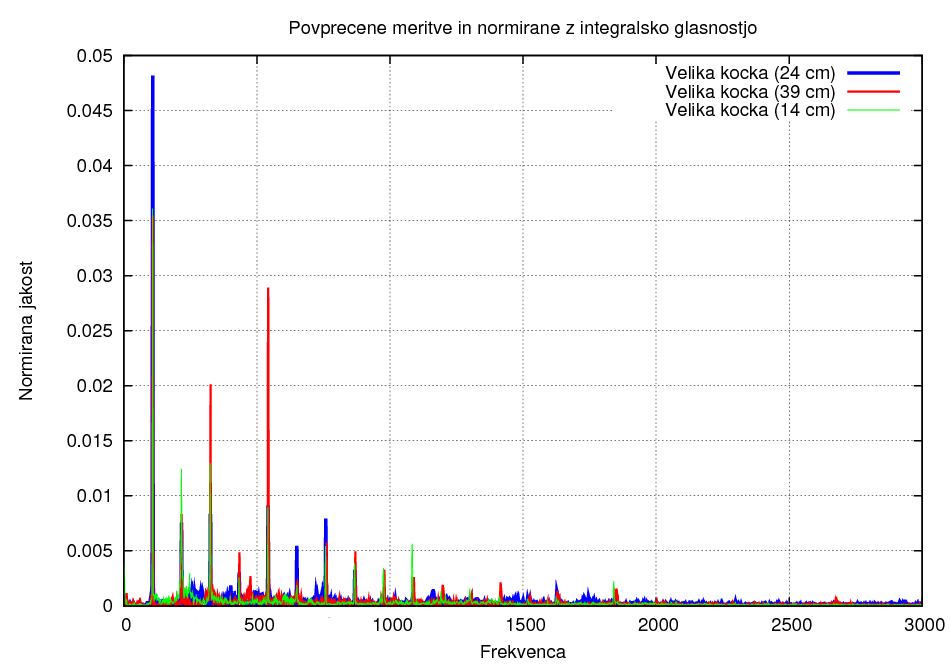
Pri tej metodi lahko ugotovimo, da ima steklo večjo zastopanost višjih frekvenc kot les, prav tako pa je to odvisno tudi od oblike, saj ima Flying v tudi večjo zastopanost višjih frekvenc kot kocka.
Meritve povprečene in pomnožene z "A-weighting" in logaritmirane
Zadnja metoda je podobna prejšni, le da je tu uporabljen tudi "A-weighting".Kaj je to "A-weighting"?
Uporablja se, zato da lahko preračunamo vse možne zvoke v tistega, ki ga dejansko sliši naše uho. Človeško uho se spreminja v občutljivosti na zapleten način, ki je odvisen od pogostosti in glasnosti. V primeru akustike, lahko A-weighting izrazimo s funkcijo RA(f), ki deluje na amplitude spektra (in ne na intenzivnost spektra), nato pa preračunamo s funkcijo A(f), ki jo uporabimo, da dobimo dejansko glasnost zvoka.
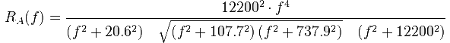
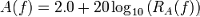
To pomeni, da amplitudo oz. glasnost pri posamezni frekvenci pomnožimo s koeficientom, ki ga podaja utežitvena krivulja (ker uho ni enako občutljivo pri vseh frekvencah), nato pa še logaritmiramo, saj je uho logaritmsko občutljivo na jakost zvoka.
Podrobnejša razlaga(angleški jezik)
Še kratka razlaga:
Sledeči grafi so dejansko slišane glasnosti v odvisnosti od frekvence.
Primerjava materialov 1:
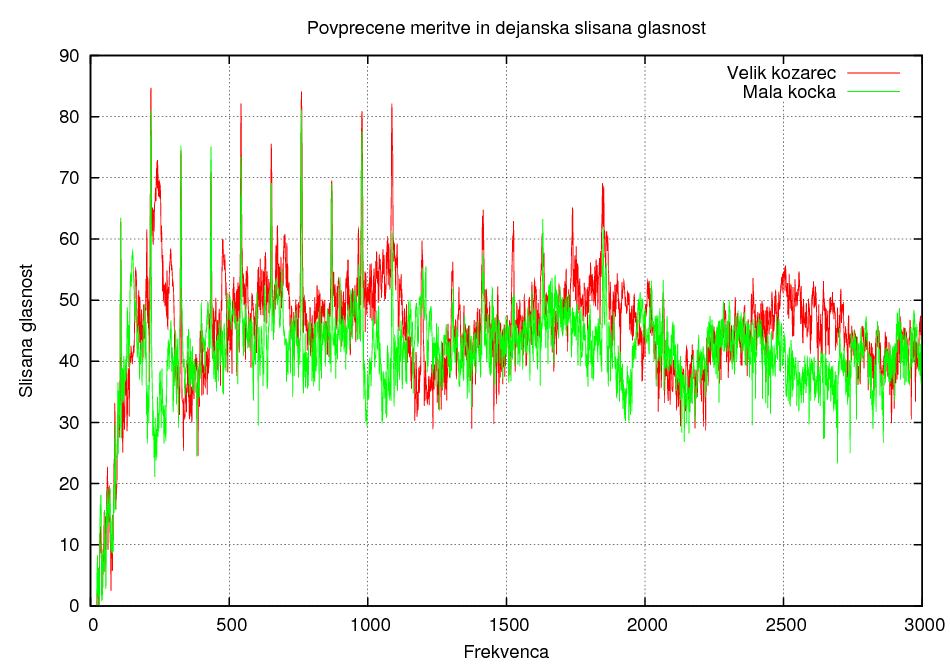
Primerjava materialov 2:
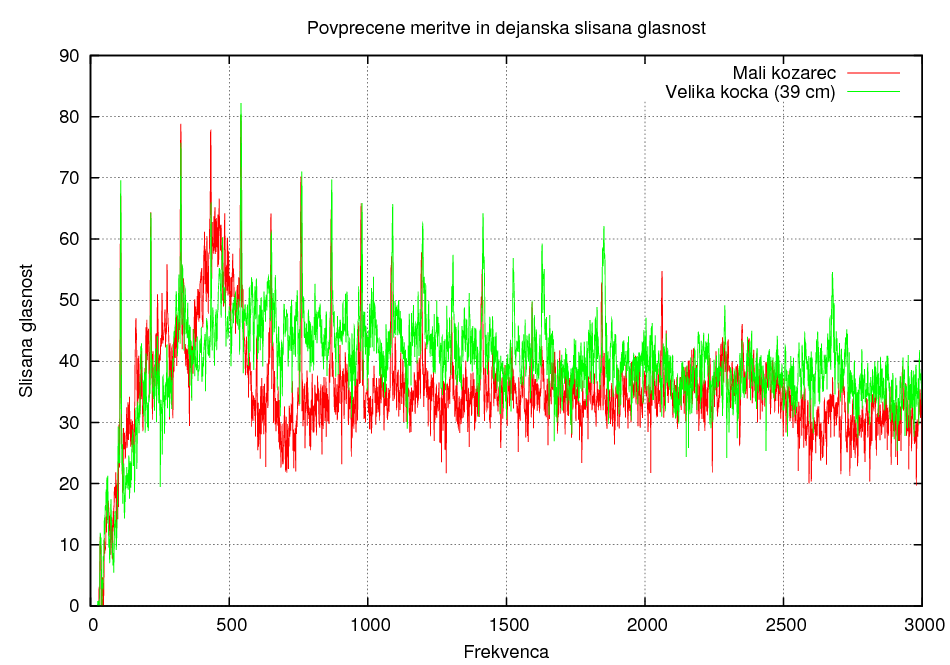
Primerjava oblik:
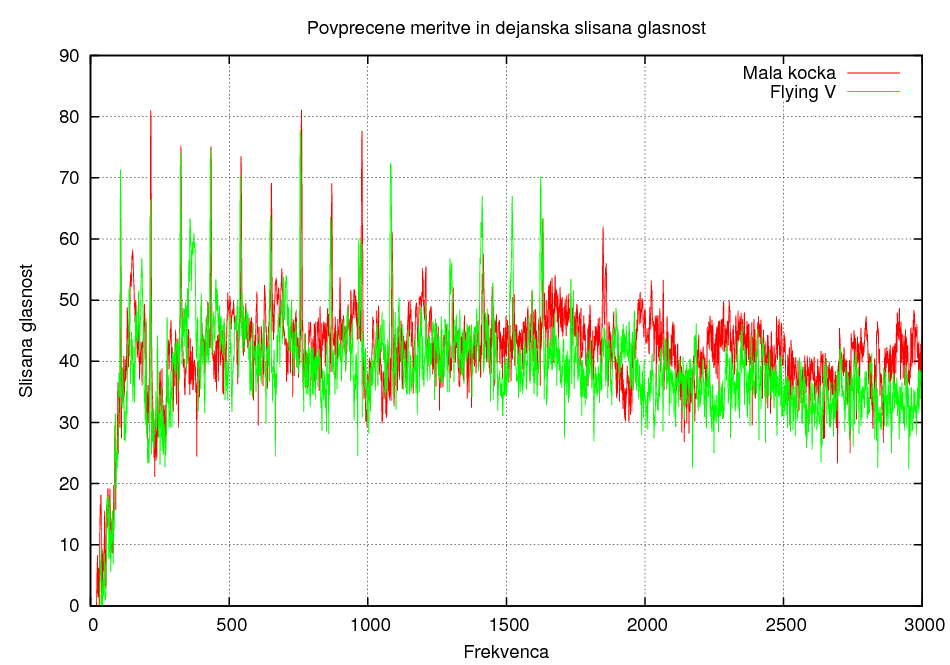
Razlika v polozaju luknje 1:
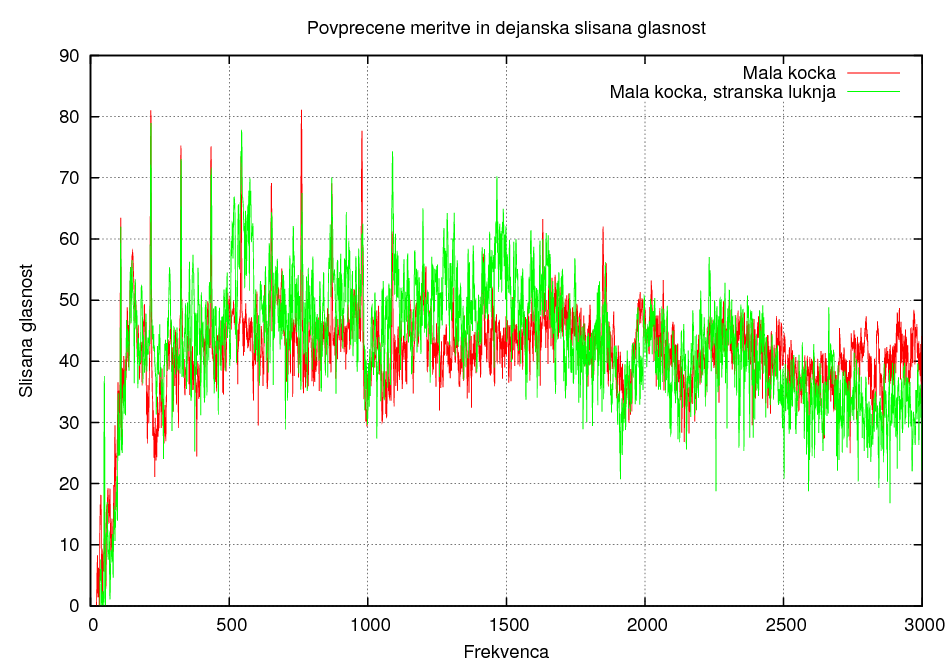
Razlika v polozaju luknje 2:
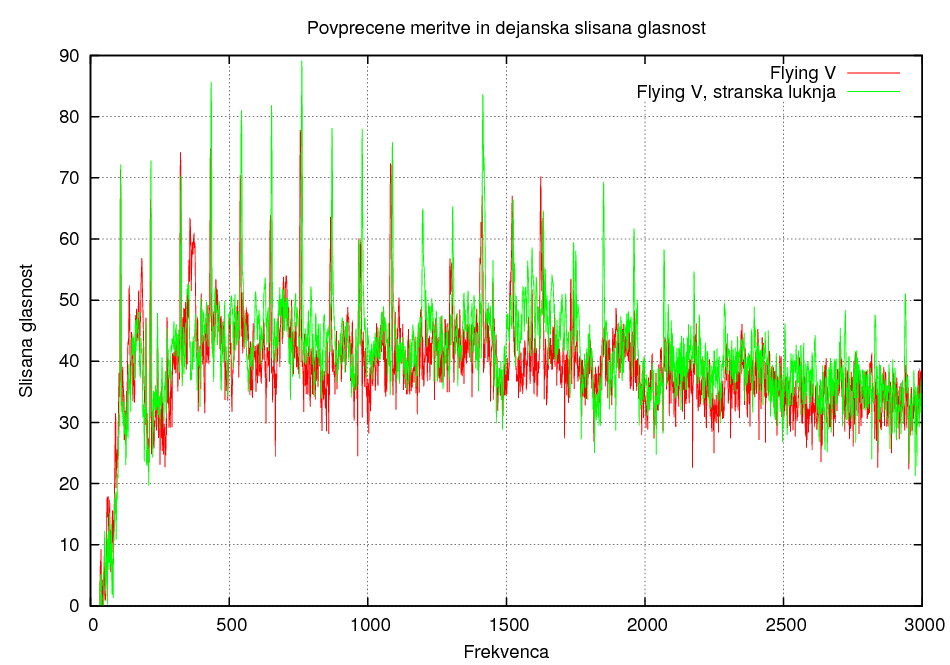
Razlika v polozaju luknje 3:
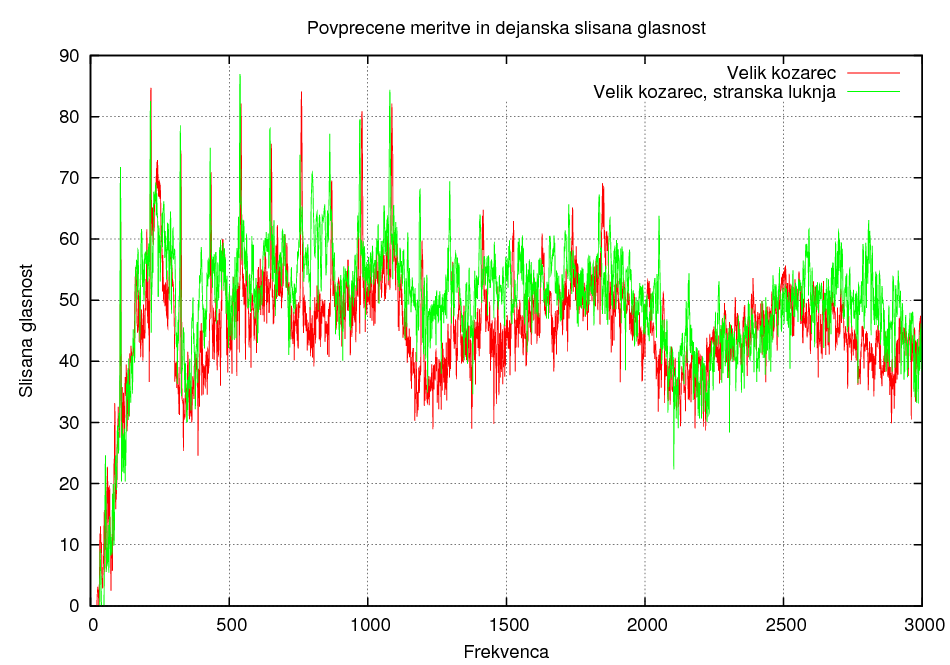
Razlika zaradi velikosti kocke:
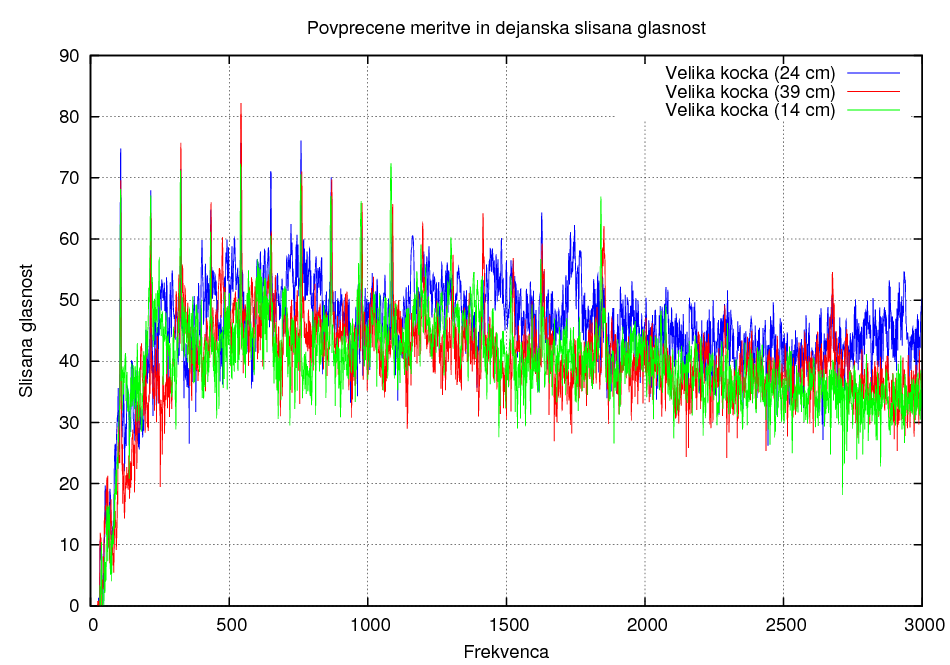
Čeprav tudi pri tej metodi ne moremo potegniti jasnih zaključkov, pa se nam zdi ta metoda boljša, saj dejansko prikažemo slišano glasnost v odvisnosti od frekvence, kar je seveda pri inštrumentih najbolj pomembno.
Zaključek
Glede na dobljene rezultate ne moremo narediti nekega konkretnega zaključka, saj so rezultati nekonsistentni. Glede na teorijo bi pričakovali, da ima večje ohišje večjo zastopanost nižjih frekvenc in manjše ohišje večjo zastopanost višjih frekvenc, v rezultatih pa lahko to le delno zasledimo. Glede na naše rezultate lahko sklepamo naslednje:- Položaj luknje vpliva na barvo zvoka, saj se pri vseh meritvah opazi večjo zastopanost višjih frekvenc pri stranski luknji.
- Rezultati povezani z velikostjo resonančnega telesa pa niso tako nedvoumni. Majhna kocka sicer ima večjo zastopanost višjih frekvenc kot velika, vendar pa je tu spet izjema velika kocka z globino 24cm, ki ima pri frekvencah okoli 1000 Hz opazno večjo zastopanost kot mala in pa velika kocka pri 39cm, ki ima v nasprotju s pričakovanji relativno majhno zastopanost nižjih frekvenc.
- Iz rezultatov bi se dalo sklepati, da material vpliva na barvo tona, steklo ima namreč relativno večjo zastopanost višjih frekvenc od lesa.