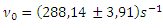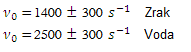ZRAK

Po teoriji bi za polzaprto cev morala veljati enačb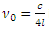a in če za c vzamemo hitrost zvoka po zraku (340 m/s), za l pa dolžino cevi (29,5 cm ± 0,1cm), dobimo, da je osnovna lastna frekvenca enaka

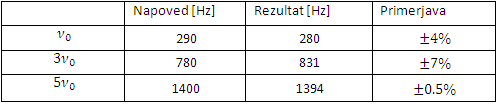
Zato bi v posnetem zvoku morala biti najbolj zastopana frekvenca oziroma njen lihi večkratnik, tj. 3ν0, 5ν0

itd. Torej:

Komentar: rezultate smo zaradi napake zaokrožili na cele vrednosti. Vse vrednosti imajo približno enako amplitudo.

VODA

Tukaj lahko izstopata dve frekvenci. Prva je frekvenca stoječega valovanja nad vodno gladino, kjer je medij zrak in jo obravnavamo kot pri polodprti cevi, druga pa je frekvenca valovanja pod gladino, kjer je medij voda in jo obravnavamo kot zaprto cev, saj se vozla (oziroma dobra približka vozlov) ustvarita na obeh koncih vodnega stolpca. Tako dobimo dve osnovni lastni frekvenci, in sicer:

V meritvah je najbolj zastopana frekvenca okoli 600 Hz, njeni dvokratnik, frekvenca okoli 1200 Hz pa se ujema z napovedjo. Ker smo merili zgolj do frekvence nekaj več kot 2 kHz, druge frekvence žal ne moremo komentirati. A ker pri 1200 Hz dobimo kar visok maksimum, smo z rezultatom vseeno lahko zadovoljni. Napaka meritve je lahko zaradi debeline cevi, vpetja cevi in drugih nepopolnosti. Pričakovali smo lahko le, da se bo ena izmed izstopajočih frekvenc ujemala z izračunano osnovno lastno frekvenco cevi. Kljub vsemu se je izbrana cev izmed vseh najbolje prilegala teoriji. Treba je tudi dodati, da smo večkratnike osnovne frekvence izbrali kot sprejemljive, ker je nihanje snovi v cevi sestavljeno iz večih frekvenc in ni nujno da je najbolj zastopana (ima največjo amplitudo) prav osnovna lastna frekvenca.

Voda z mehurčki

Pri prvi jakosti zračne črpalke, kjer je bil volumski pretok enak 0,00785 l/s, so bile najbolj izstopajoče frekvence pri 90 in 360 Hz, sledili sta jima pa še 1600 ter 2100 Hz. Teoretična napoved za tak volumski pretok je, da je osnovna lastna frekvenca 115 Hz (vir [2] pri temperaturi 23.5 stopinj Celzija in razmerju volumnov 0,00787, hirost zvoka je 136 m/s). To je napoved, če na vodni gladini ne nastane vozel. S tem rezultatom smo kar zadovoljni, saj se frekvenca 90 Hz lepo ujema z napovedjo, prav tako pa se 360 Hz ujema s trikratnikom napovedane osnovne lastne frekvence.

Pri drugi jakosti črpalke, z volumskim pretokom 0,0249 l/s, je bila teoretična napoved osnovne lastne frekvence 65 Hz, če ne nastane vozel, oziroma 130 Hz, če vozel nastane (vir [2] pri temperaturi 23.5 stopinj Celzija in razmerju volumnov 0,0249, hirost zvoka je 77 m/s). Najbolj zastopane vrednosti frekvenc so pa bile 360, 450, 590 in 1200 Hz, v tem vrstnem redu od največje do najmanjše amplitude. Tukaj se ujema frekvenca 360 Hz s trikratnikom 130 Hz. Kot že rečeno, ne moremo biti prepričani o vozlu na odprtem delu cevi, zato je tudi napoved malo manj omejujoča, a vseeno smo lahko zadovoljni za ujemanjem teorije in rezultatov.