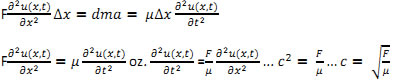Za nas se je zdela najbolj primerna situacija, da merimo Dopplerjev efekt, ko se izvir približuje sprejemniku. Meritve smo si razdelili na več setov in za vsak set smo se odločili za različne »hitrosti« izvira. Hitrost je tu v narekovaju, saj se dejansko nič ni premikalo, pa vendar smo naredili isti učinek kot bi se premikal izvir. Najprej smo vzbudili val na nekem kraju in nato čez nekaj časa spet na drugem kraju – povprečna hitrost izvira bi na tem intervalu bila kar razlika leg krajev vzbuditve deljeno s časovnim intervalom med vzbuditvima.
Narisali smo več grafov:
odvisnost razmerja nove(večje) frekvence in frekvence vzbuditve valovanja:
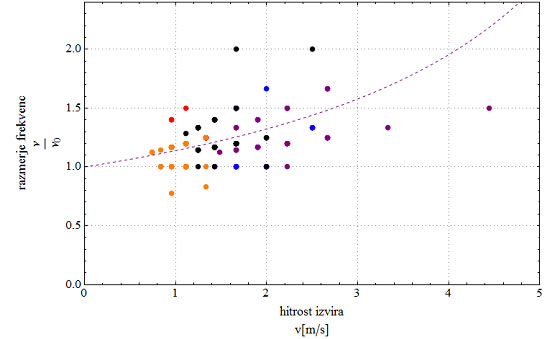
V tem grafu se vidi, da s povečano hitrostjo narašča razmerje med frekvenco, ki jo zaznavamo in frekvenco oddajanja. (1.0 pomeni, da zaznamo isto frekvenco, kot je bila oddana, 2.0 pa da je zazna frekvenca 2x večja od oddane). Pike predstavljajo naše meritve, črtkana črta pa predstavlja krivuljo, ki ima pol pri hitrosti valovanja vrvi.
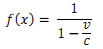
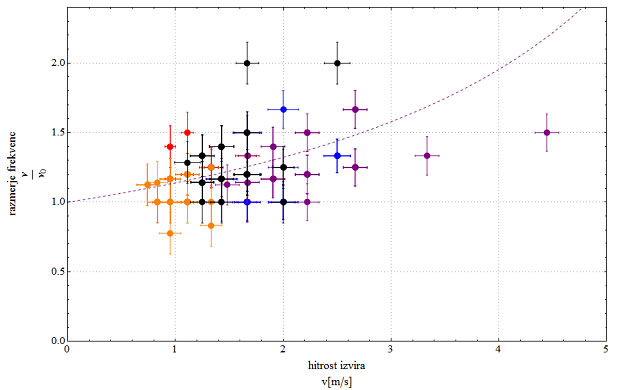
Na osi x je nanešena hitrost izvira, ki smo jo izračunali glede na zamik in razdaljo med udarcema vzbujanja. Na osi y pa je razmerje med frekvencama – ν, ki smo jo določili z razliko med časoma prvega in drugega vzbujanja in frekvenco ν0, ki smo jo določili z razliko med časoma, ko sta prvi in drugi
val prešla mesto merjenja.
In še isti graf, upoštevajoč napake pri merjenju:
odvisnost med eksperimentalno izmerjenimi razmerji frekvenc in teoretično-eksperimentalnim določenimi razmerji frekvenc:
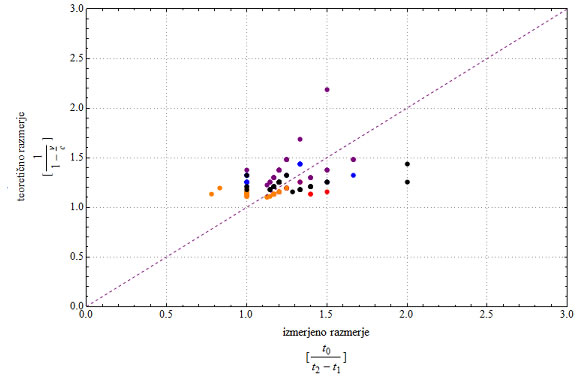
Tu je teoretično razmerje določeno z enačbo, ki jo poznamo že od prej in za katero smo rabili vedeti samo hitrost valovanja (v) in hitrost premikanja vira vzbujanja valovanja (c). Izmerjeno razmerje pa je razmerje med časom ko valova prideta na mesto merjenja (t0) in časom, ki je minil od ene do druge vzbuditve (t2 – t1). Črtkana črta prikazuje naše domneve, da naj bi bili ti razmerji isti – ob določenem teoretičnem razmerju hitosti, naj bi dobili isto razmerje časov. Iz grafa se vidi, da sta razmerji (z manjšimi odstopanji) dokaj isti.
odvisnost med samimi frekvencami (teoretičnimi in eksperimentalnimi):
Še obrnjeni odvisnost zadnjega grafa:
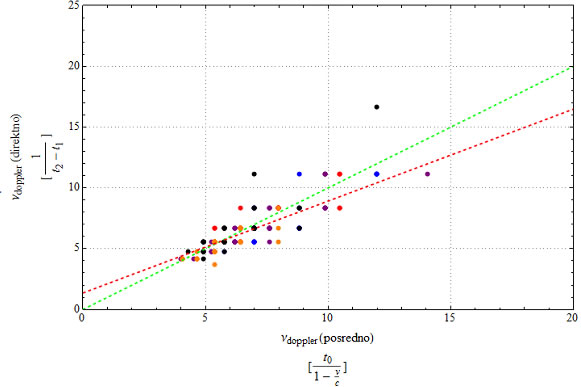
Na zadnjih treh grafih predstavlja linearna črta funkcijo f(x)=x . S to funkcijo lahko preverimo, kako se eksperimentalni rezultat ujema s teoretičnim (, ki je še vedno delno eksperimentalni). V primeru dobrega ujemanja, se razmerja prilegajo omenjeni funkciji.
Pri naših meritvah so točke precej razpršene okoli te premice, pa vendar se lahko vidi nek trend v tej smeri. Pri zadnjem grafu smo dodali še rdečo črtkano črto, ki pomeni najboljšo premico, ki se prilega tem izmerjenim točkam (metoda najmanjših kvadratov). Dobimo funkcijo f(x)=1,3+0,76x.
Zanimiv podatek o meritvah je tudi medsebojna korelacija:
S pomočje programa Mathematice smo z ukazom Correlation [νDoppler(posredno), νDoppler(direktno)] dobili, da je korelacija 0,78, ki je dokaj podobna koeficientu premice. Pove, da se vrednosti načeloma višajo, ko povečujemo argument funkcije.
Lahko si pogledamo še histogram vrednosti razmerja [νDoppler(posredno), νDoppler(direktno)]
Merjenje Hitrosti vrvi:
Eksperimentalno:
S hitro kamero smo si večkrat posneli kako hitro potuje val. Zavedali smo se, da vrv ne sme biti preveč napeta, saj bi bila potem hitrost razširjanja valovanja prevelika, da bi lahko opazili kakšen Dopplerjev efekt.
Povprečje izmerjenih vrednosti: 
Standardna deviacija meritev: 
c = 
Relativna napaka meritve: 
Opazili smo, da hitrost ni prevelika in bomo lahko generirali valove, ki se s hitrostjo lahko primerjajo.
*Teoretično-eksperimentalno:
Iz teorije smo vedeli, da ima hitrost po vrvi izražavo: 
kjer je F sila, s katero je napeta vrv in μ dolžinska masna gostota vrvi, definirana kot
, kjer je m masa vrvi in l dolžina vrvi.
Naš namen je bil eksperimentalno izmeriti te tri količine – silo, maso in dolžino, ter nato vstaviti v enačbo in na koncu primerjati z eksperimentalno določeno vrednostjo.
Meritve:
Izmerjena sila s pomočjo škripca in uteži:
mu= 0,299kg + 0,001 kg
Masa vrvi:
mv= 0,128kg + 0,001kg
Dolžina vrvi:
lv= 4,34m + 0,04m
Radij škripca:
r= 0,075m + 0,005m
Dolžina vrvi, ki je visela čez škripec:
l= 0,75m + 0,01m
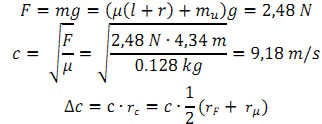
relativna napaka meritve sile: rF= 
relativna napaka meritve dolžinske gostote: rμ= 
Hitrosti se zadovoljivo ujemata.
*Izpeljava enačbe za silo, ki je napenjala vrv pri naši meritvi:
Člena mu in μ⋅l sta v enačbi, saj oba povzročata silo, ki direktno vleče vrv.
Izpeljimo še člen μ⋅r , kjer je r-radij škripca:
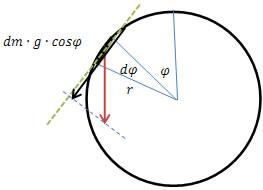
Sešteti moramo vse koščke vrvi od kota φ= 0 do φ= π/2, pri tem pa upoštevati projekcijo na tangento v tisti točki.
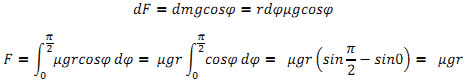
Od tod pride člen μgr, ki sicer ni velik.
* Izpeljava hitrosti valovanja po vrvi:
Če si ogledamo vrv, ki je napeta s silo med krajem x+Δx in x z maso Δm.
Odmik vrvi je ob času t na x enak u(x) na x+Δx pa u(x+Δx).
Lahko zapišemo 2. Newtonov zakon:
F(x+Δx ) – F(x) = dma, kjer je a pospešek 
Ker gledamo vrv na zelo kratkem krajevnem intervalu, lahko tangens kota nadomestimo kar z argumentnom. Projekcija F na prečno smer pri x+Δx : F(x+Δx ) = 
pri x pa 
Ta deluje na zelo majhen košček vrvi z maso dm= μΔx
