Teorija

Določanje gostote vode glede na njeno višino

 

Gostota vode pred poskusom (brez mehurčkov) je:

,

kjer je masa vode, višina vode in osnovna ploskev valjaste posode.


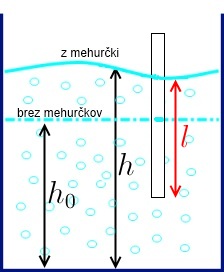
Če v tekočino (vodo) dovajamo zrak, nastajajo mehurčki, povprečna gostota tekočine pa pade, saj se volumen tekočine poveča (nivo se dvigne), medtem ko masa ostane ista (maso zraka zanemarimo). Ko potopimo v vodo plovec, se višina vode še dodatno dvigne. V valjasti posodi lahko izračunamo novo gostoto tekočine :



kjer je višina vodne gladine, dolžina potopljenega dela plovca in osnovna ploskev plovca.


Iz zgornjih enačb sledi:



Pri našem poskusu je bila osnovna ploskev posode S = 855 cm2, višina vode se je gibala okoli
h = 51 cm, višina potopljenega dela večjega plovca l = 40 cm in njegova osnovna ploskev
A = 4, 5 cm2. Sledi:



vidimo, da je člen zanemarljivo majhen, torej je končna enačba za računanje gostote vode:



S pomočjo te enačbe smo določali gostoto vode v odvisnosti od tlaka v cevi glede na višino vode.

 

Sledi:

 

,
kjer je , kjer je tlak v cevi, ki dovaja zrak.

 

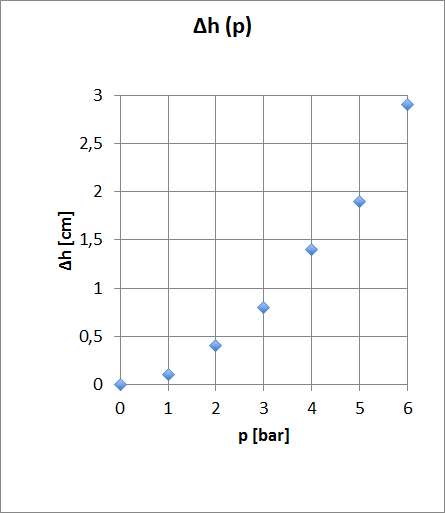
Sprememba višine vode glede na tlak v cevi


Če narišemo graf spremembe višine vode v odvisnosti od tlaka v cevi, vidimo da velja:

 

 

Za odvisnost višine od toka smo si pomagali s tem, da smo kvadrirali vrednosti tlaka in jih na grafu primerjali vrednostmi višine vode. Iz tega smo dobili kar lepo premico, zato smo sklepali da je kvadratno odvisno. Lahko bi poskusili z drugimi odvisnostmi, vendar se nam ne zdi vredno, saj zveza ni tako pomembna za končne dokaze.


Torej velja:



in iz enačbe ob predpostavki sledi:
.

Določanje gostote vode glede na potopljenost plovca

 

Brez sile upora

 

Na telo deluje sila teže :



kjer je masa telesa in težnostni pospešek.

 

Če neko telo potopimo v tekočino, bo nanj delovala sila vzgona :

 

,

kjer je gostota tekočine, v kateri je predmet in volumen izpodrinjene tekočine.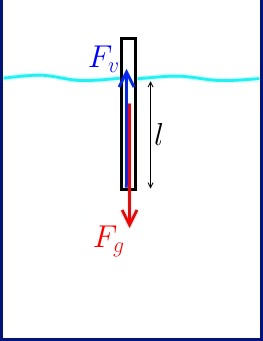

 

Če telo miruje, morata biti sili nasprotno enaki, torej:

 

 

Večja kot je masa telesa, večji volumen telesa se bo moral potopiti, da bosta sili v ravnotežju. Če naše telo aproksimiramo z navpičnim valjem, sledi:


,

kjer je višina potopljenega dela, gostota izpodrinjene tekočine in osnovna ploskev plovca.

 

Če enačbo obrnemo, lahko izračunamo gostoto tekočine:


.


S to enačbo smo računali gostoto glede na potopljenost plovca.

 

Manjša kot je gostota tekočine, bolj se bo telo potopilo.

 

Z upoštevanjem sile upora

 

Rezultati pa ne odražajo nujno samo gostote tekočine. Mehurčki se zaletavajo v telo in ga dvigujejo, prav tako se jih nekaj “zalepi” na dno predmeta in mu tako navidezno povečajo volumen.
Ocenjujemo, da so ti popravki manjši od napake meritve.

 

Smer navzgor

 

Če pa mehurčki niso enakomerno razporejeni, dobimo efekt fontane, kjer je vodna gladina nekje bolj dvignjena kot drugod. To se zgodi, ker se mehurčki po vodi ne gibljejo brez upora in vlečejo vodo za seboj. Če je plovec na vrhu fontane, deluje nanj sila , tako da velja:

 

.

 

V tem primeru je sila vzgona manjša, zato bi odčitali manjši , saj nismo upoštevali. Iz izračunov bi sledilo .

 

Smer navzdol

 

Tokovi ki nastanejo v sredi fontane in dvigujejo plovec, pa se vračajo na dno ob straneh posode. Ker je sredina fontane višje od roba, predmet z nje zdrsne in tokovi ga vlečejo navdol s silo .
Torej velja:


.

 

Sila vzgona je tu večja, za kar se mora telo bolj potopiti, mi pa odčitamo večji . Sledilo bi
.

 

Več zraka kot dodamo, več bo mehurčkov, močnejši bodo tokovi in predmet se bo še bolj potopil.


Na naše rezultate bi lahko vplivalo tudi nenatančno odmerjanje, toda ker vse tri meritve s plovci nakazujejo zelo podoben trend, trdimo, da je ravno zaradi vpliva tokov.

Določanje gostote glede na potonitev plovca

 

Če telesu spreminjamo maso, spreminjamo tudi njegovo povprečno gostoto , ki je


,
kjer je volumen telesa.

 

To smo storili tako, da smo v plastenko natočili različne nivoje vode.

 

Telo bo potonilo, ko bo povprečna gostota tekočine manjša od gostote telesa. V trenutku, ko telo nima več stika z zrakom, a še vedno ne pade na dno, je njegova gostota enaka gostoti vode, torej:

 

,

 

kjer je gostota vode merjena glede na potonitev plovca. S to enačbo smo določali .