Eksperiment
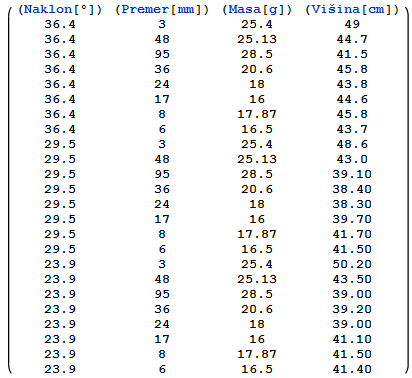
| Ime kroglice | A | B | C | D | E | F | G | H | Premer[mm] | 3 | 48 | 95 | 36 | 24 | 17 | 8 | 6 | Masa[g] | 25.4 | 25.13 | 28.5 | 20.6 | 18 | 16 | 17.87 | 16.5 | Višina[36.4°,cm] | 49.00 | 44.70 | 41.50 | 45.80 | 43.80 | 44.60 | 45.80 | 43.70 | Višina[28.5°,cm] | 48,60 | 43.00 | 39.10 | 38.40 | 38.30 | 39.70 | 41.70 | 41.50 | Višina[23.9°,cm] | 50,20 | 43.50 | 39.00 | 39.20 | 39.00 | 41.10 | 41.50 | 41.40 |
- A = Prozorna votla k
- B = Miškina k.
- C = 4.Kovinska k. (največja)
- D = 3.Kovinska k.
- E = 2.Kovinska k.
- F = 1.Kovinska k. (najmanjša)
- G = Frnikula prozorna k.>
- H = Frnikula bela k.
Teoretični graf nam bo prikazal kako naj bi se obnašala odvisnost potrebne višine kroglice z odvisnostjo od njenih parametrov izmerjenih v zavihku meritve. Za polno analitični analizo uporabimo energijski zakon izspeljan v zavihku teorija.
Spodnja 3D slika mam prikazuje ravno to! Točke ki definirajo spodnjo ploskev nam povejo potrebno teoretično začetno višino kroglice da opravi po naši definiciji cel "luping". Enačba ki jo definira je prikazana nad pripadajočo sliko.
Modra črta nam predstavlja našo 3D teoretično ploskev pri fiksnem radiju "looping" zanke. V okolici to črte bi teoretično morali eksperimentalno izmeriti potrebne začetne višine kroglic. To teorijo bomo uporabili za nadalno analizo, ko bomo opisovali naš sistem.
![]()
Kliki na sliko za interaktivno obračanje
Zdaj se usmerimo na črtkano krivuljo. Opisali bomo samo krivuljo ki ustreza primernemu radiju naši looping zanki.

V nadaljevanju bomo ugotovili da je opis meritev z zgornjim grafom povesem napačen. Vendarle poskusimo opisati minimum, ki ga opazimo na grafu.
Razlaga za tako odvisnost se skriva v vstrajnostnem momentu kateri je povezan z kinetično energijo. Vstrajnostni moment doda kvadratno odvisnost v enačbo, to lahko opazimo v enačbi, ki opisuje 3D ploskev na začetku teoretične analize.
Izračunajmo še stacionarno točko:
![]()
![]()
Zgoraj je podana stacionarna točka samo kot zanimivost. Stacionarna točka je primerna samo za levo rešiitev odvoda. Opazimo da pri majhnih radijih lahko opišemo potrebno višino z limitnim računom (h = 5/2 R). Ta rezultat pa smo izspeljali ko smo upoštevali energijski zakon brez vstrajnostnega momenta. V limitnem primeru smo zanemarili radij to ima posledico da zanemarimo vstrajnostni moment.
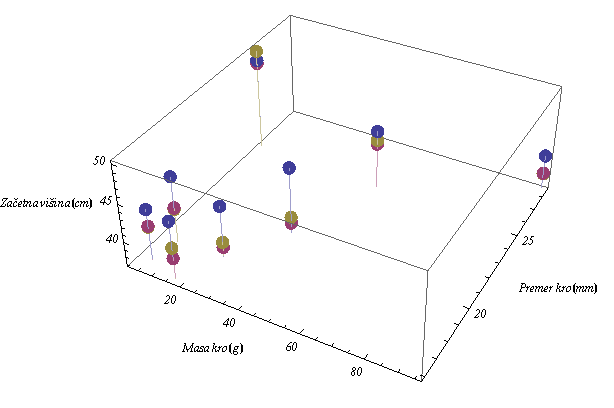
Na spodnji sliki so prikazani podatki tabele čisto na začetku strani, te smo zmerili pri projektnem delu.
V prostoru ki ga definira baza parametrov kroglice: { masa, premer, potrebna minimalna višina za uspešen "looping" } vidimo naše meritve. Različne barve kroglic prikazujejo meritve pri različnih kotih rampe.
Kliki na sliko za interaktivno obračanje
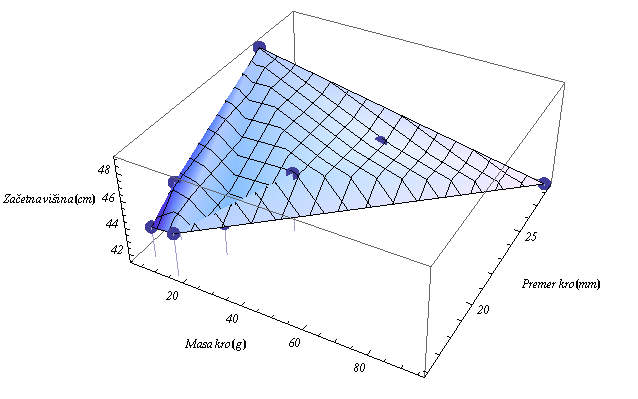
Spodnji graf nam prikazuje meritve pri izbranem kotu rampe. S tem grafom želim prikazati, da meritve v priblišku ležijo na ravnini, z drugačnimi besedami meritve nimajo neke nore odvisnosti. To je pomembno ko bomo opisovali meritve z približano funkcijo ("FITTOM"), saj lahko vsako krivuljo, ploskev opišemo v prvem priblišku z pripadajočim odvodom (GLEJ: Taylorjeva vrsta)
Kliki na sliko za interaktivno obračanje
V nadaljevanju bom prikazal 2 postopka analize. Najprej bom predstavil analizo z napredno metodo opisovanja podatkov v več dimenzijskem prostoru. Nato bom prikazal analizo meritev gledalcem z slabšim predznanjem matematike.
Vsak zajem podatkov lahko predstavimo v vektorskem prostoru, katerega določimo z bazo vektorjev naših merjenih spremenljivk v našem primeru so to parametri kroglice { masa , premer , začetna višina kroglice, in stopinski kot vstopa kroglice } . Vsako meritev si lahko predstavljamo kot vektor kateri nosi podatke o izvedeni meritvi. Ta vektor si lahko predstavljamo kot točko v 4D prostoru. Če je težava kako bi si lahko to predstavljali si lahko zamislimo 3D prostorom v katerem je vsaka točka še utežena z "maso" po domače bi si lahko zamislili da opisujemo 3D prostoru gostoto nehomogenega telesa. Cilj te analize je opisati povezano telo v 4D prostoru ali po domače gostoto v 3D prostoru. Za začetek prikažimo vektorje meritev z naslednjo matriko, en vektor meritve je ena vrstica naslednje matrike. Stolpci predstavljajo izmerjene parametre meritve.
Ko imamo definirane podatke lahko naredimo "polinomski fit na podatke" s katerim bomo opisali naš objekt v 4D prostoru. Ponavadi se prilagaja podatkom z linearno ali eksponentno krivuljo vendar nam Tayilorjeva teorija in GRAF EKSPERIMENTALNIH MERITEV kaže da lahko prilagodimo tudi polinomski funkciji. Zraven tega nam še TEORETIČNA PLOSKEV prikazuje da bi morala biti funkcija podatkov dokaj enostavna.
V mathematici imamo zelo močna orodja na tem področju, eno med temi je FindFit. To funkcijo uporabimo za opis naših podatkov...
fit = FindFit[dat,
c1 + c2*Φ + c3*Φ^2 +
c4 + c5*P + c6*P^2 +
c7 + c8*M + c9*M^2,
{c1, c2, c3, c4, c5, c6, c7, c8, c9}, {Φ, P, M}]
V spremenljivki dat imamo našo matriko z VEKTORJI MERITEV.
Rezultat analize
c1 -> 32.2345, c2 -> -2.75471, c3 -> 0.0496636,
c4 -> 32.2345, c5 -> -0.0734561, c6 -> -0.000838727,
c7 -> 32.2345, c8 -> -2.18755, c9 -> 0.0698397
Ti koelificienti nam opišejo formulo uporabljeno v FindFit funkciji:
V = c1 + c2 ? + c3 ?^2 + c4 + c5 P + c6 P^2 + c7 + c8 M + c9 M^2
Pri čemer moramo paziti na enote spremenljivk! Vhodne spremenljivke morajo imeti enake enote kot prva vrstica VEKTORJI MERITEV. S to formulo smo popolno opisali potrebno višino kroglice na rampi glede na vhodne parametre kroglice in klanca. Več o približevanju podatkov v več dimenzijonalnih prostorih si lahko preberete na LINKU.
Kot vsak rezultat bi morali preveriti z teoretično krivuljo, vendar to je v našem primeru brez pomena saj zaradi velike množice pojavou, ki so opisani v zavihku teorija nam rezultat močno odstopa od teoretičnega rezultata.
Za osnovno analizo sem se odločil da predstavim meritve v 2D prostoru. V glavnem bom probal izluščiti informacije iz naslednjih grafov :
- Višina z odvisnostjo mase
- Višina z odvisnostjo premera žogice
- Višina z odvisnostjo kota rampe
1 Visina z odvisnostjo mase
.png)
Na zgornjem grafu vidimo, da so podatki tako razmetani, da nemoramo opaziti nobene močne odvisnosti, saj so ostali parametri kroglic dovolj pomembni da odvisnost ni samo odvisna od naše spremenljivke. Graf edino kaže, da se pri večjem naklonu rampe potrebna višina krogliceo poveča. To odvisnost pojasnimo z zadevanjem kroglice ko napravi prehod iz rampe v looping.
2 Visina z odvisnostjo premera
.png)
Na zgornjem grafu opazimo zanimiv trend, ki nakazuje da večja kroglica potrebuje večjo začetno višino na rampi za večji kot rampe. To si lahko razlagamo z naslednjo teorijo. Vemo že iz prejšega grafa, da kroglica pri prehodu iz rampe v "looping" izgubi veliko hitrosti, poleg tega se kroglica zadeva od rob poti in je zaradi spina vpliv na skupno energijo kroglice toliko večji. Zato je trend dokaj logičen in razložljiv.
3 Visina z odvisnostjo kota vstopa
.png)
Na zgornjem grafu opazimo dokaj šibko odvisnost vendar odstaja. Največjo odvisnost od kota vidimo pri 1.kovinski kroglici, ki je najmanjša med štirimi kovinskimi kroglicami. To bi si spet lahko razlagamo z prehodom v "looping" na katerem kroglice izgubljajo svojo energijo. Ta trend opazimo za vse kroglice.
Opazimo lahko tudi zelo visoko potrebno višino prozorne krogljice. Razlago smo že podali v zavihku teoriji, kjer smo opisali, da bodo imele lahke kroglice velik problem z uporom zraka.