EKSPERIMENT

PRVO SREČANJE, 6.11.2013

Naloga je od nas zahtevala, da ugotovimo in izmerimo časovno odvisnost spreminjanja vodne gladine v poljubno oblikovani posodi, če voda izteka ali priteka v posodo s konstantnim pretokom. Naše meritve smo morali primerjati še z izračunano časovno odvisnostjo za izbrane oblike posod.

Izhajali smo iz različnih idej, kako bi lahko v posodo dovajali vodo s konstantnim pretokom. Izbrali smo si zadnjo idejo, da bi s pomočjo cevi pritrjene na pipo voda pritekala v posodo (odtekanju smo se hoteli posvetiti naknadno).

Poskušali smo postaviti okvirno postavitev, da bi ugotovili, kako bomo najlažje dobili kvalitetne rezultate. Ugotovili smo, da bomo potrebovali ravno podlago, na katero bomo postavili posodo (najraje belo) in pa temno ozadje, da bomo lahko dobro videli višino gladine vode, ki bo pritekala v posodo. Poleg tega smo potrebovali še stojalo, s pomočjo katerega bi lahko na stalni višini s kamero na telefonu snemali naraščanje gladine.

Drugi problem, na katerega smo naleteli, je bil kako preveriti, da je pretok konstanten in da bo tak tudi skozi celoten eksperiment. Zato pa med eksperimentom ne bi smeli zapirati pipe. Preverili smo zanesljivost naše pipe. Nekajkrat smo z dvema štoparicama izmerili čas, ki je bil potreben za to, da smo napolnili 1,77 litrsko čašo. Ugotovili smo, da so se pri štirih (osmih) meritvah časi dobro ujemali. Časi so podani v spodnji tabeli (1.tabela).

1. tabela: poskusne meritve časa napolnitve 1,77 litrske čaše.
MERITEV	1. štoparica	2. štoparica
1.	14.29 s	14.23 s
2.	14.24 s	14.23
3.	14.26 s	14.25 s
4.	14.22 s	14.24 s

Poskusno smo posneli eksperiment s čašo. Ugotovili smo, da je cev potrebno držati ob robu notranje posode, da curek lepo teče do dna, sicer gladina zaradi curka niha in ni možno dovolj natančno določiti višine gladine.

Na prvem srečanju smo s pomočjo kljunastega merila izmerili še premere in višine posod, katere smo uporabili na naslednjem srečanju.

ČAŠA

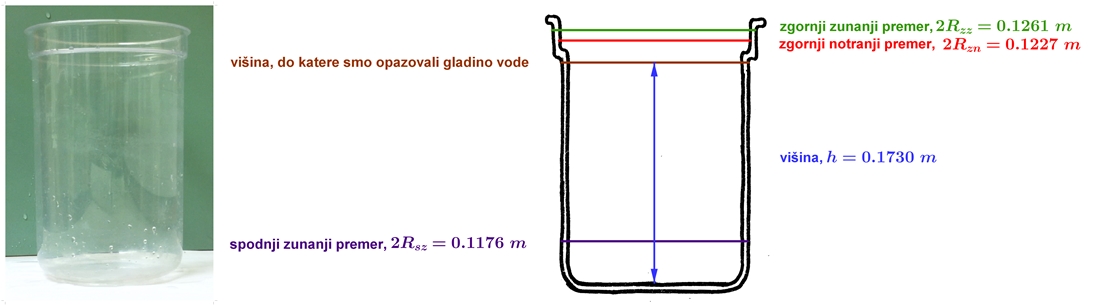
Višino gladine vode smo opazovali do označene rjave črte. Do te črte ima čaša stalen polmer. S pomočjo izmerjenih meritev v zgornjem delu čaše smo lahko izračunali njeno debelino roba:

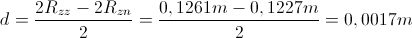
Odtod pa lahko izračunamo notranji polmer čaše:

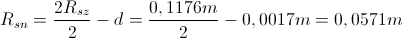
ERLENMAJERICA

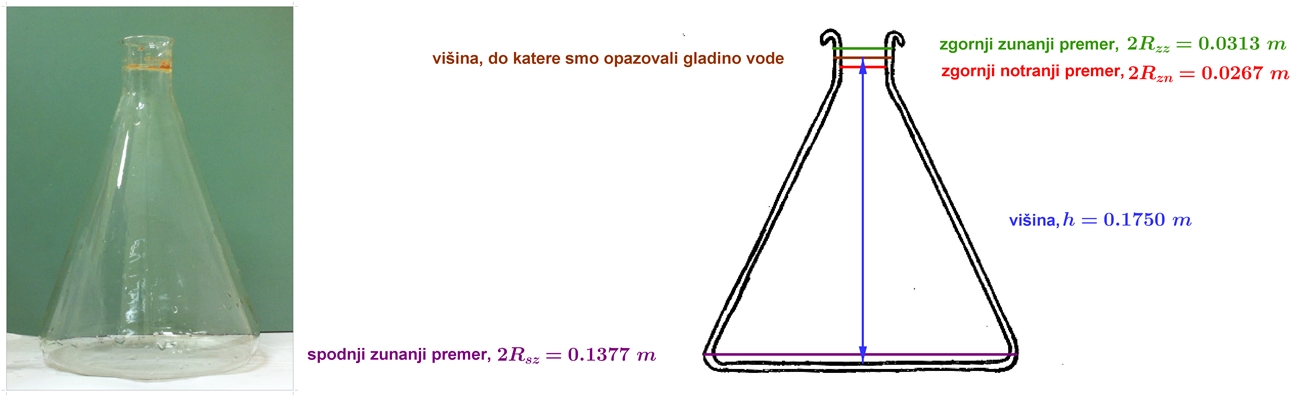
Višino gladine smo opazovali do zgornje rjave črte. Kot pri čaši smo izračunali debelino roba erlenmajerice:

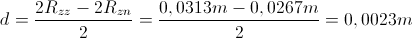
Nato pa še spodnji notranji polmer erlenmajerice:

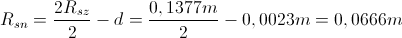
BUČKA

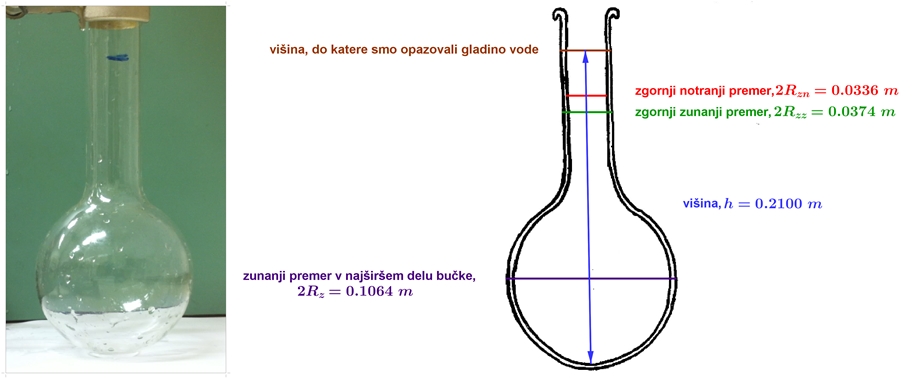
Pri bučki smo višino gladine opazovali do rjave črte. Podobno kot pri čaši in erlenmajerici smo izračunali notranji premer bučke v spodnjem najširšem delu:

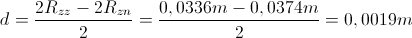
Odtod:

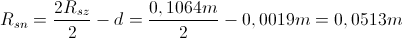
DRUGO SREČANJE, 13.11.2013

Na drugem srečanju smo s kamero na telefonu, ki je bil pritrjen na stojalu, posneli poskuse z različnimi posodami. Pretok smo izračunali s pomočjo meritev pri čaši. Tokrat smo si izbrali manjši curek, saj smo tako lahko bolj natančno izmerili čas, ki je bil potreben, da se je gladina vode dvignila do označene črte.

ČAŠA

Posneli smo dva poskusa.

2. tabela: meritve časa napolnitve 1,77 litrske čaše.
MERITEV	1. štoparica	2. štoparica
1.	122.8 s	122.5 s
2.	123.8 s	124.5 s

S pomočjo meritev iz prvega srečanja smo izračunali volumen čaše:

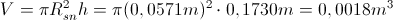
Odtod smo potem izračunali pretok, ki smo ga upoštevali pri vseh nadaljnih eksperimentih:

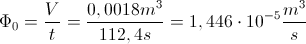
Čas smo izbrali glede na meritve prvega posnetka, ki se je dobro ujemal tudi z meritvami obeh štoparic.

ERLENMAJERICA

Posneli smo dva poskusa.

3. tabela: meritve časa napolnitve erlenmajerice
MERITEV	1. štoparica	2. štoparica
1.	78.09 s	78.99 s
2.	77.99 s	78.54 s

BUČKA

Posneli smo dva poskusa.

4. tabela: meritve časa napolnitve bučke
MERITEV	1. štoparica	2. štoparica
1.	46.12 s	45.89 s
2.	45.77 s	45.60 s

TRETJE SREČANJE, 20.11.2013

Na tretjem, zadnjem srečanju smo posnetke obdelali v programu Logger Pro in izrisane grafe naraščanja višine gladine v odvisnosti od časa primerjali z izračunanimi funkcijami.

ČAŠA

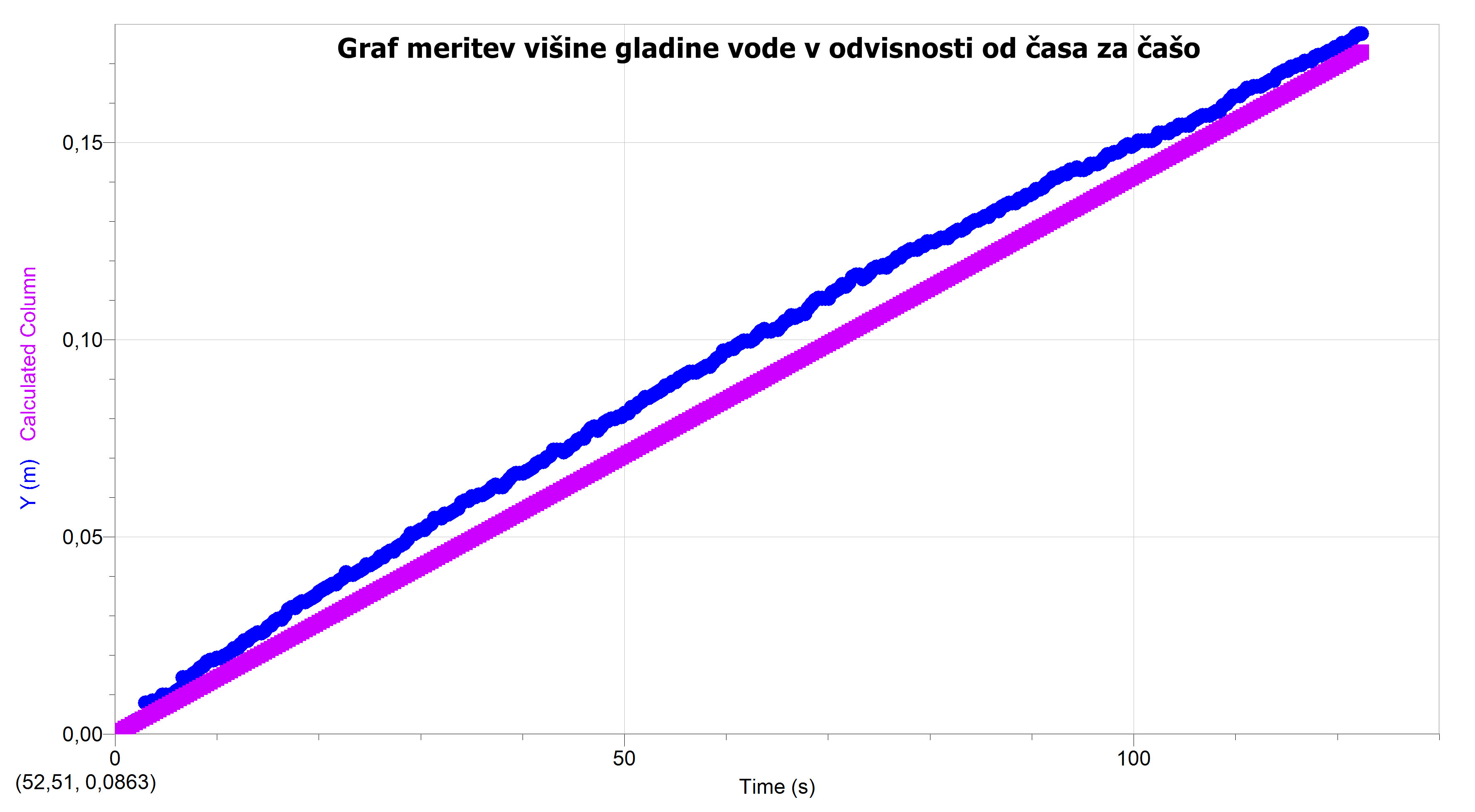
Najprej smo izrazili spreminjanje višine gladine v odvisnosti od časa za čašo:

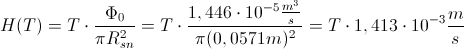
Primerjava meritev (modra črta) in izračunana (roza črta):

ERLENMAJERICA

Pri erlenmajerici smo najprej izrisali graf meritev s pomočjo posnetka.

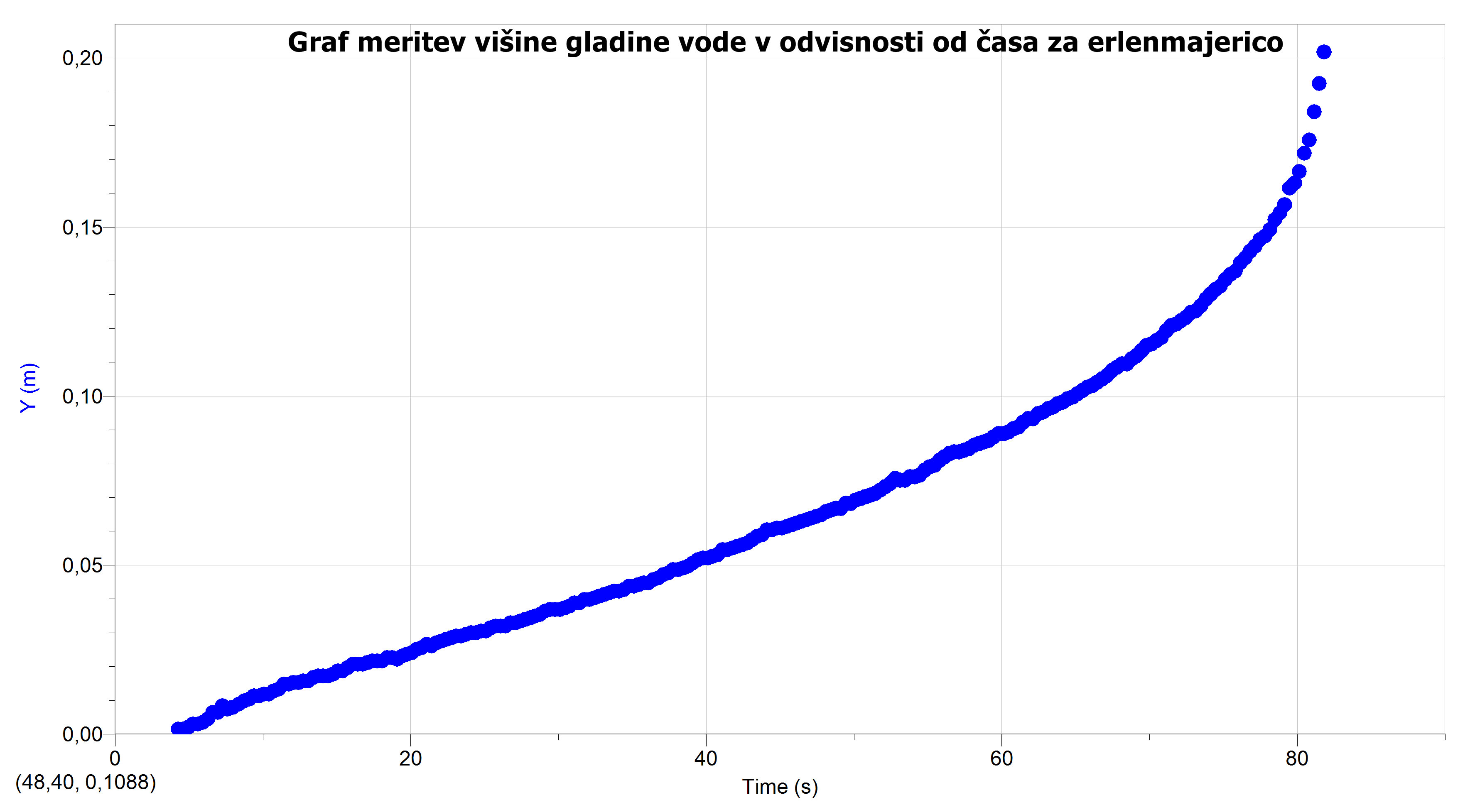
Ugotovili smo, da se naša izračunana formula ne more ujemati s to meritvijo, saj smo formulo izpeljali s predpostavko, da ima erlenmajerica obliko prisekanega stožca. Zato smo se osredotočili na del grafa, ki prikazuje erlenmajerico brez vratu.

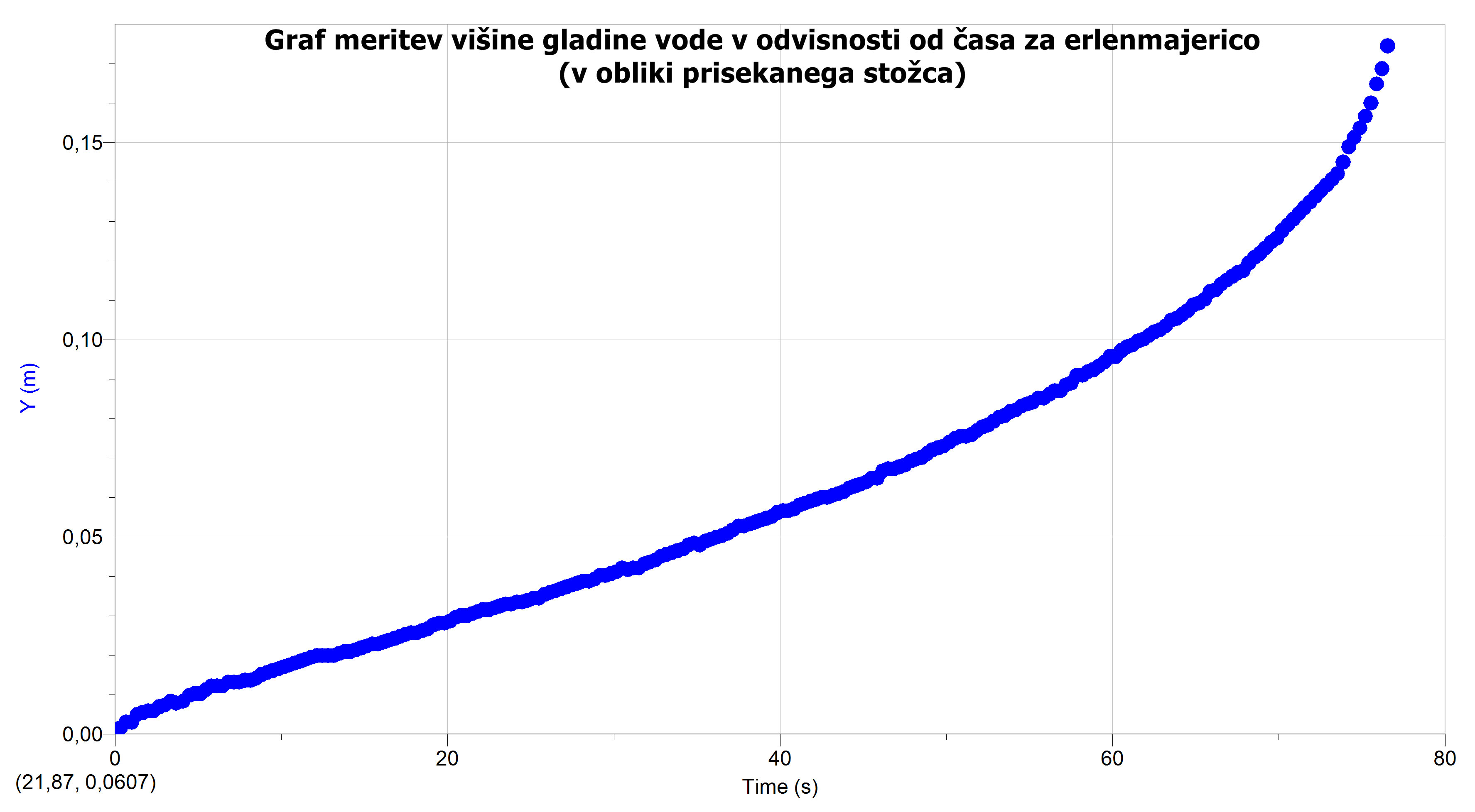
Tudi spodnji del erlenmajerice ni pravilne oblike. Izmerili smo na kateri višini se začne in konča prisekani stožec.

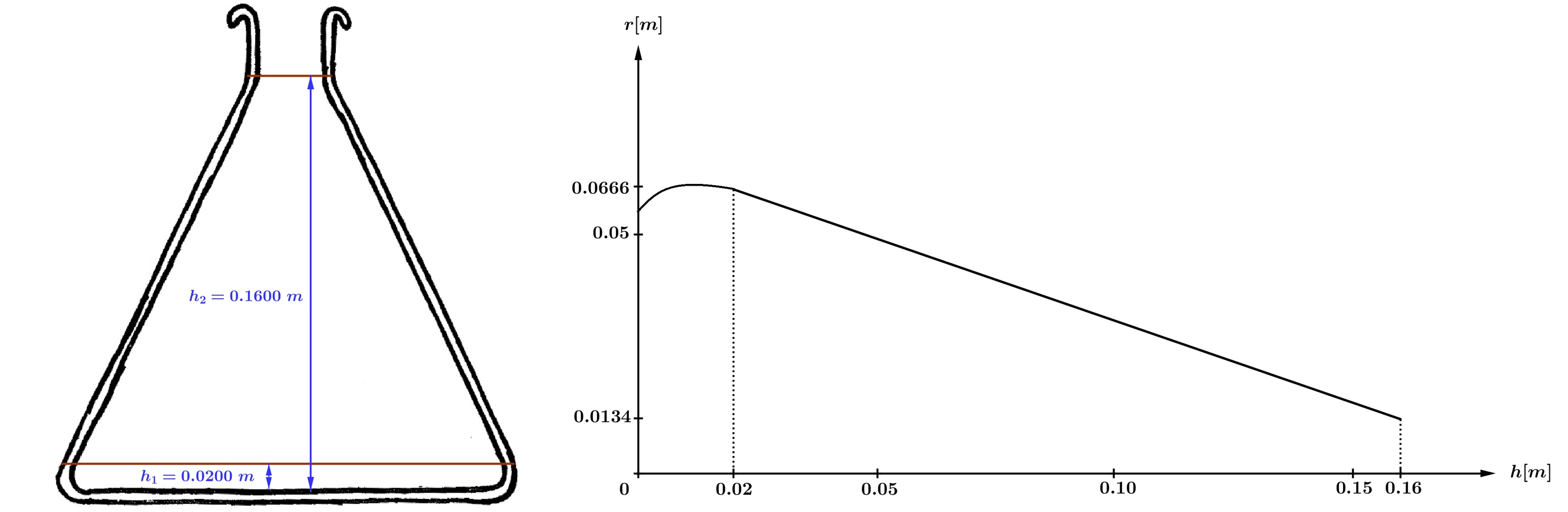
Formulo izpeljemo s pomočjo skice:

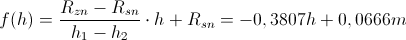
V zgornji formuli je 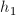višina do dna prisekanega stožca in 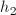višina do začetka vratu.

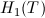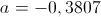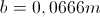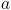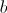Upoštevamo izraz za . Iz prejšnje formule dobimo in . Vstavimo in v :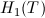

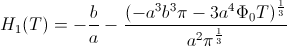
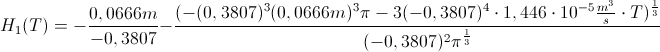
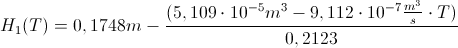
Ponovno smo s pomočjo posnetka izrisali graf meritev prisekanega stožca in to potem primerjali še z izračunano formulo.

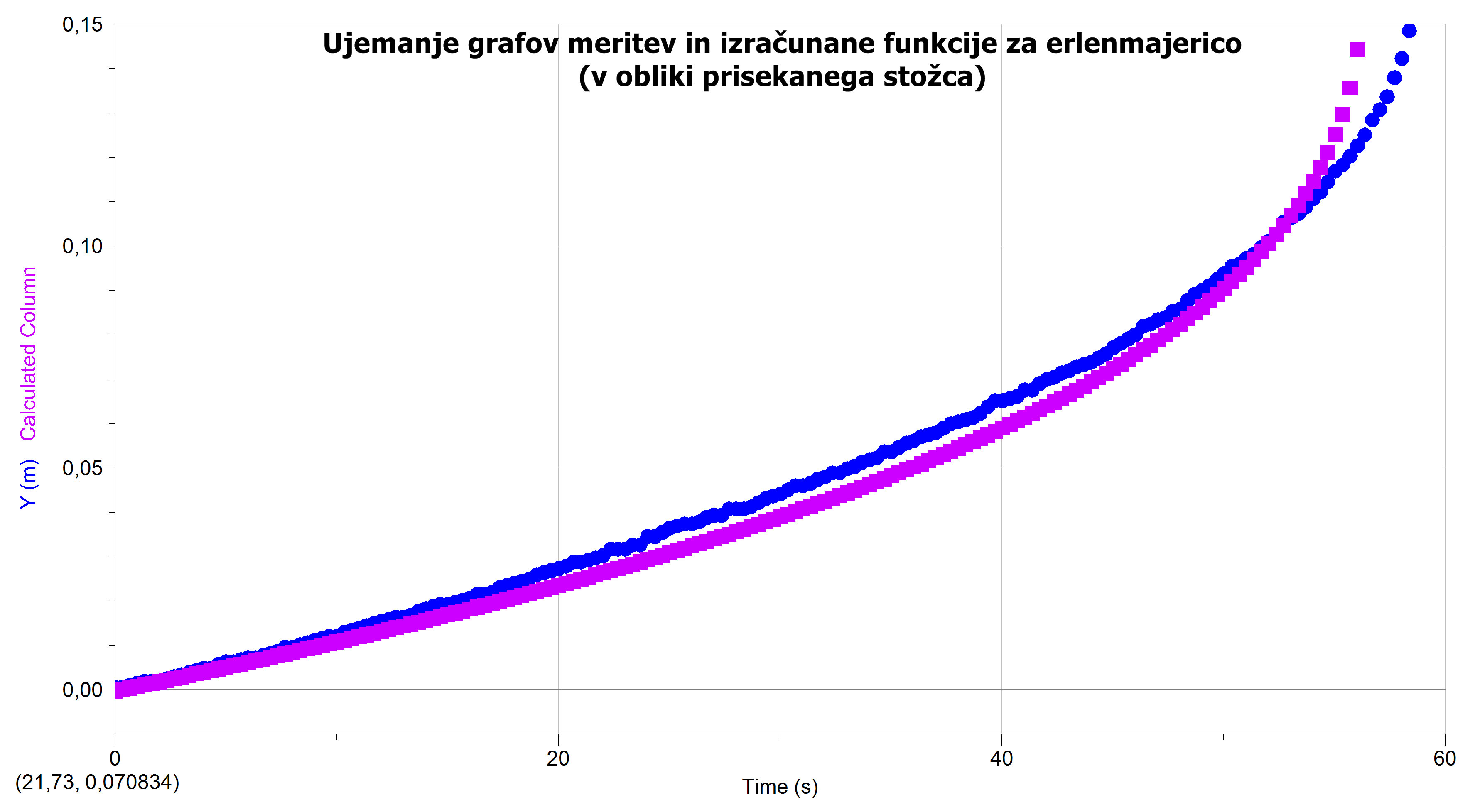
BUČKA

S pomočjo posnetka smo izrisali graf bučke:

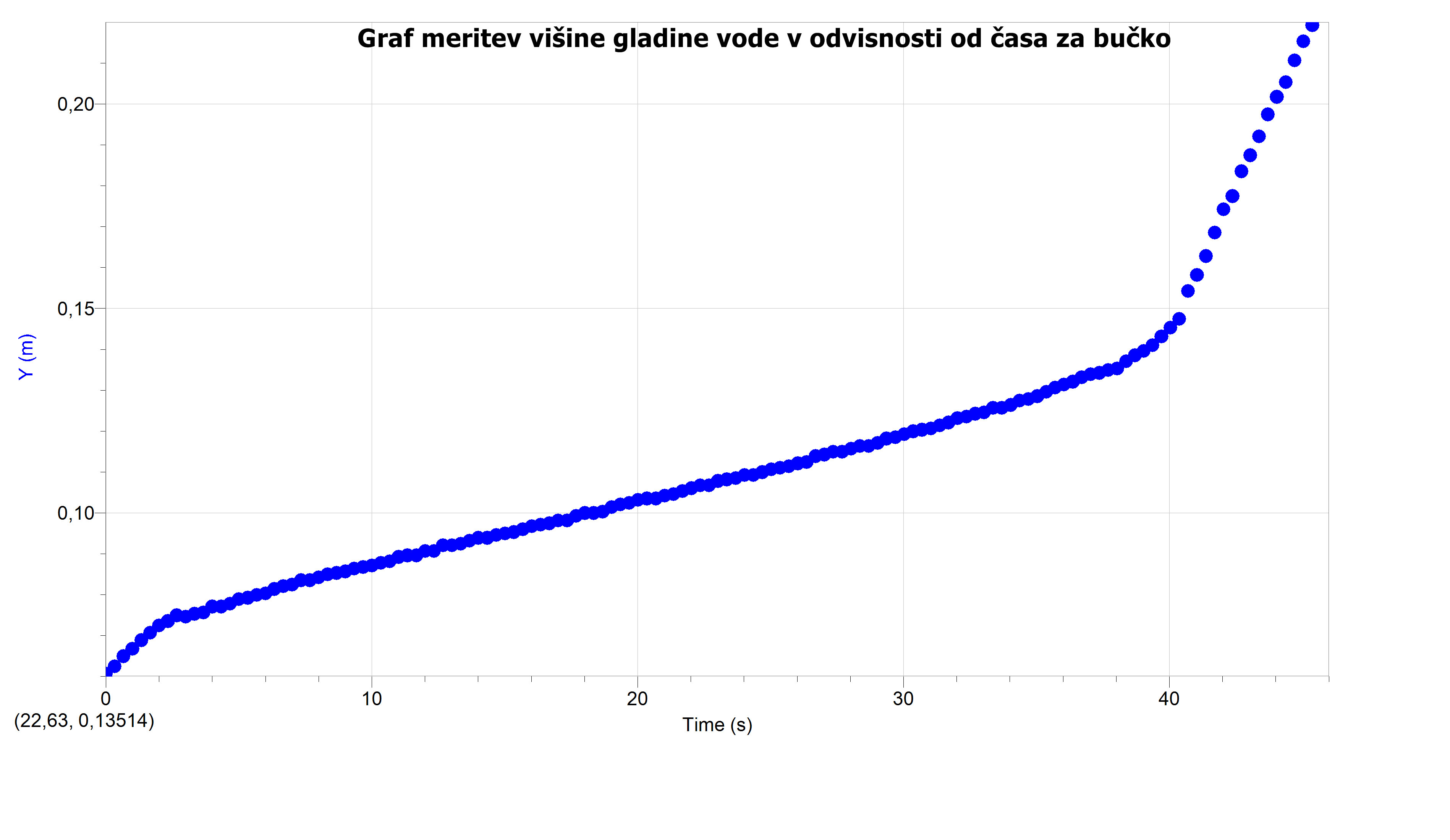
Podobno kot pri erlenmajerici se tudi pri bučki naša funkcija višine v odvisnosti od časa ni ujemala z izrisanim grafom, ker smo pri izračunu formule upoštevali samo obliko krogle, ne pa tudi vratu, ki prav tako sestavlja bučko. Zato bomo naraščanje grafa opazovali do vrha okroglega dela (brez vratu). Funkcija

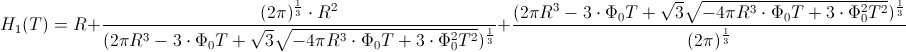
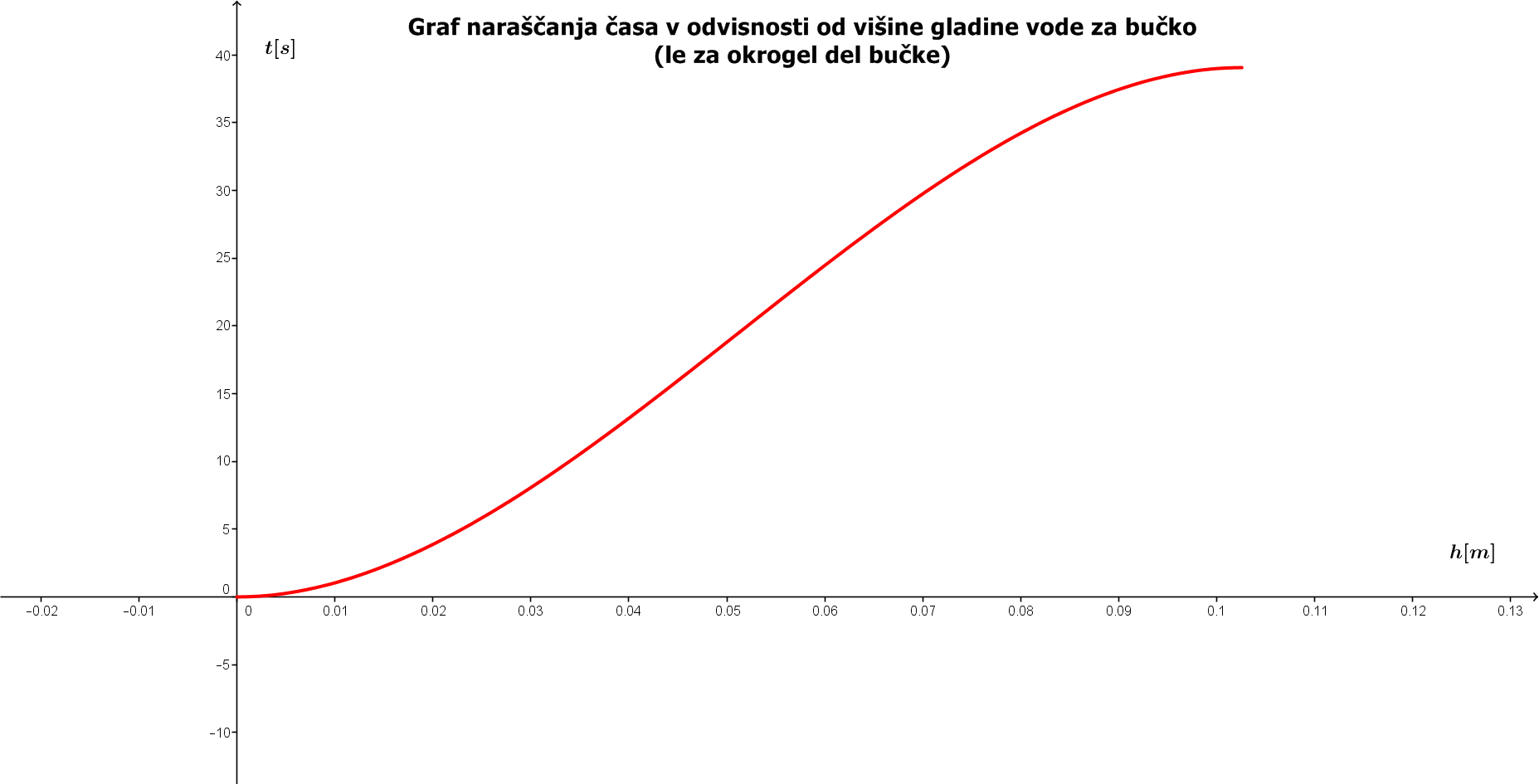
ki velja za ta del in smo jo izračunali, se nam v programu ni hotela izrisati. Zato smo najprej narisali funkcijo naraščanja časa v odvisnosti od višine (izračunana pri teoriji), ki izgleda takole:

Če to funkcijo zrcalimo preko simetrale lihih kvadrantov, dobimo graf funkcije višine v odvisnosti od časa:

Tako bi morala izgledati naša inverzna funkcija. Če primerjamo to funkcijo z izrisano funkcijo, ki jo dobimo pri bučki, vidimo da se oblika ujema. Torej smo izračunali pravilno funkcijo višine, ki jo dobimo pri dolivanju vode v bučko.