NAPOLNIMO ČAŠE
TEORIJA
Za ugotavljanje, če so meritve pri eksperimentu prave, potrebujemo teoretično poznavanje eksperimenta in nekakšen vpogled, kako naj bi meritve izgledale.
Začnemo z enačbo
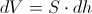 ,
,
kjer je 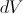 sprememba prostornine,
sprememba prostornine,
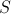 površina gladine na trenutni višini posode in
površina gladine na trenutni višini posode in
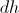 sprememba višine. Naše posode imajo vse
tako obliko, da je površina gladine vedno okrogle oblike. Zato za vse posode lahko zapišemo enačbo površine
sprememba višine. Naše posode imajo vse
tako obliko, da je površina gladine vedno okrogle oblike. Zato za vse posode lahko zapišemo enačbo površine
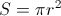 ,
,
kjer je  radij površine in
radij površine in
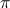 konstantno število pi.
konstantno število pi.
Radij površine se pri posamezni posodi drugače spreminja v odvisnosti od višine posode. Zato bomo označili spreminjanje radija kot funkcijo v odvisnosti od višine posode:
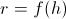
Če to vstavimo v zgornjo enačbo za površino in vse vstavimo v prvo enačbo spremembe volumna, dobimo:
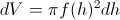
Enačbo nato delimo s spremembo časa
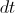 :
:
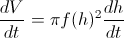
Spomnimo se, da je pretok (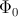 ) ravno sprememba volumna
v nekem časovnem intervalu:
) ravno sprememba volumna
v nekem časovnem intervalu:
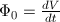 . To upoštevamo pri zgornji enačbi
in celotno enačbo pomnožimo z
. To upoštevamo pri zgornji enačbi
in celotno enačbo pomnožimo z
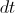 ter dobimo:
ter dobimo:
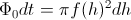
Upoštevamo, da je pretok konstanten in integriramo zgornjo enačbo:
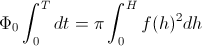
V zgornji enačbi je 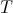 čas, ki poteče od začetka eksperimenta, in
čas, ki poteče od začetka eksperimenta, in
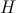 višina vodne gladine po času
višina vodne gladine po času
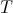 .
.
ČAŠA
Za čašo velja, da se radij površine ne spreminja. Zato je naš radij
 konstanten oz. funkcija
konstanten oz. funkcija
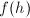 je konstantna in enaka
je konstantna in enaka
 .
Zato jo lahko nesemo pred integral:
.
Zato jo lahko nesemo pred integral:
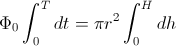
Po integraciji dobimo enačbo
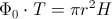 ,
,
iz katere izrazimo višino gladine
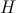 in dobimo funkcijo višine
v odvisnosti od časa
in dobimo funkcijo višine
v odvisnosti od časa 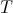 :
:
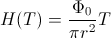
To funkcijo smo uporabili za preverjanje meritev pri eksperimentu.
ERLENMAJERICA
Ker je erlenmajerica stožaste oblike, se radij površine spreminja linearno z višino gladine. Zato lahko zapišemo zvezo med radijem in višino z naslednjo enačbo:
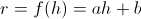
V zgornji enačbi je
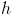 trenutna višina posode,
trenutna višina posode,
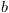 radij dna erlenmajerice
radij dna erlenmajerice
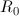 in
in
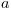 kvocient med razliko radijem vrata erlenmajerice
kvocient med razliko radijem vrata erlenmajerice
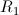 in
radijem dna erlenmajerice ter dolžino od dna do začetka vrata erlenmajerice
in
radijem dna erlenmajerice ter dolžino od dna do začetka vrata erlenmajerice
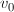 :
:
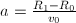
Enačbo za radij vstavimo pod integral in dobimo:
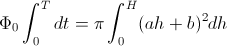
Ko zgornjo enačbo integriramo dobimo:
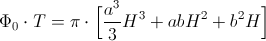
Iz te enačbe je težje izraziti višino
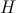 , zato smo si pomagali s programom Mathematica in sicer s
funkcijo Solve. Dobimo naslednje izražave višine s časom:
, zato smo si pomagali s programom Mathematica in sicer s
funkcijo Solve. Dobimo naslednje izražave višine s časom:
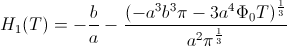
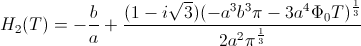
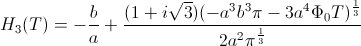
Ker je samo
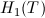 realna funkcija, smo jo izbrali za funkcijo
za preverjanje meritev pri eksprimentu.
realna funkcija, smo jo izbrali za funkcijo
za preverjanje meritev pri eksprimentu.
BUČKA
Za bučko je malo težje izraziti radij, saj je okrogle oblike. Zato si predstavljamo, da bučko razrežemo po sredini in zapišemo enačbo krožnice v odvisnosti od trenutne višine posode in radija gladine:
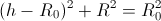
V zgornji enačbi je
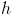 trenutna višina posode,
trenutna višina posode,
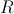 radij gladine in
radij gladine in
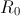 radij bučke.
Iz enačbe izrazimo radij gladine:
radij bučke.
Iz enačbe izrazimo radij gladine:
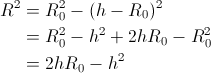
Tako dobimo, da se radij gladine spreminja s funkcijo
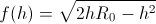 .
.
Zgornjo funkcijo vstavimo pod integral in dobimo:
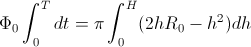
Po integraciji dobimo enačbo
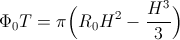 ,
,
iz katere je težko izraziti višino
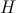 . Tudi tu si pomagamo s programom
Mathematica in sicer s funkcijo Solve. Dobimo naslednje izražave:
. Tudi tu si pomagamo s programom
Mathematica in sicer s funkcijo Solve. Dobimo naslednje izražave:
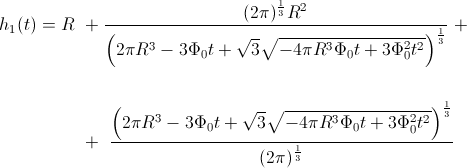
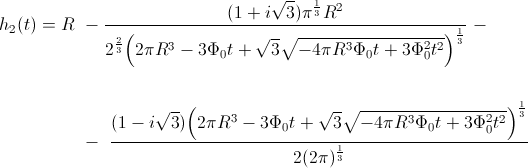
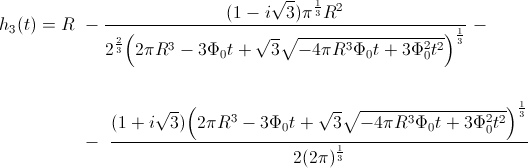
V zgornjih funkcijah so zdaj
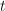 čas, ki je potekel od začetka eksperimenta,
čas, ki je potekel od začetka eksperimenta,
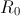 radij bučke in
radij bučke in
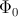 pretok. Ker je samo
pretok. Ker je samo
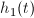 realna funkcija, smo jo izbrali za funkcijo
za preverjanje meritev pri eksprimentu.
realna funkcija, smo jo izbrali za funkcijo
za preverjanje meritev pri eksprimentu.