Analiza gibanja
Za vzorčni primer gibanja vzemimo centrifugirko z maso 32 g, z 2 luknjama s premerom 2,35 mm. Zaradi majhne mase, majhnega števila lukenj in majhne velikosti lukenj, je to ena izmed najpočasneje potapljajočih se centrifugirk. Preverili smo tudi grafe nekaterih ostalih ponovitev. Ti imajo podobno obliko.
Graf lege v odvisnosti od časa naredimo iz podatkov, ki smo jih izluščili iz posnetka. Graf hitrosti in pospeška pa ustvarimo z enkratnim in dvakratnim diskretnim odvajanjem.
Iz grafov in posnetka je razvidno, da posoda ob potapljanju tudi dušeno niha. Opazimo, da je pospešek sorazmeren z odmikom od ravnovesne lege. Ravnovesna lega se v našem primeru premika, saj se posoda med nihanjem tudi potaplja. Smer pospeška kaže v nasproti smeri odmika, kar je skladno z matematičnim opisom nihanja. Nihanje je dušeno, saj je amplituda odmika z vsakim nihajem manjša.
Do nihanja pride zaradi načina spuščanja centrifugirk v tekočino. Da bi zagotovili enake začetne pogoje pri vsakem spuščanju, smo spuščali iz držala iz lego kock. Pri tem smo počakali, da sta se zunanja in notranja gladina vode izenačili. Med potapljanjem smo opazili, da je notranja gladina vode vedno nekoliko nižje kot zunanja, razlika višin pa se s časom povečuje. Ko je teža centrifugirke in vode znotraj centrifugirke enaka vzgonu vode in uporu, se posoda giblje premo enakomerno. Opazimo, da posoda ne niha v primeru, ko je notranja gladina vode nižje glede na zunanjo gladino vode. Zaradi dodatne obtežitve je gostota posode večja od gostote vode. Da se posoda giblje nepospešeno, mora biti notranja gladina gotovo nižje. Torej je enaka notranja in zunanja začetna gladina vzrok za nihanje. Nihanju se je pri poskusih s centrifugirkami nemogoče izogniti, saj je nemogoče izpustiti centrifugirko v trenutku, ko sta gladini v takem razmerju, da od začetka ne niha. Tudi če nam bi uspelo zmanjšati nihanje z spuščanjem pred izenačitvijo obeh gladin, ta metoda ne bi bila ustrezna, saj ni ponovljiva.
Posoda niha tudi v smereh, ki so vzporedne z gladino vode. Slutimo, da to nihanje na rezultate ne vpliva zelo pomembno, saj je amplituda relativno majhna.
Video 3: Posnetek potapljanja z GoPro kamero. Posnetek je upočasnjen.
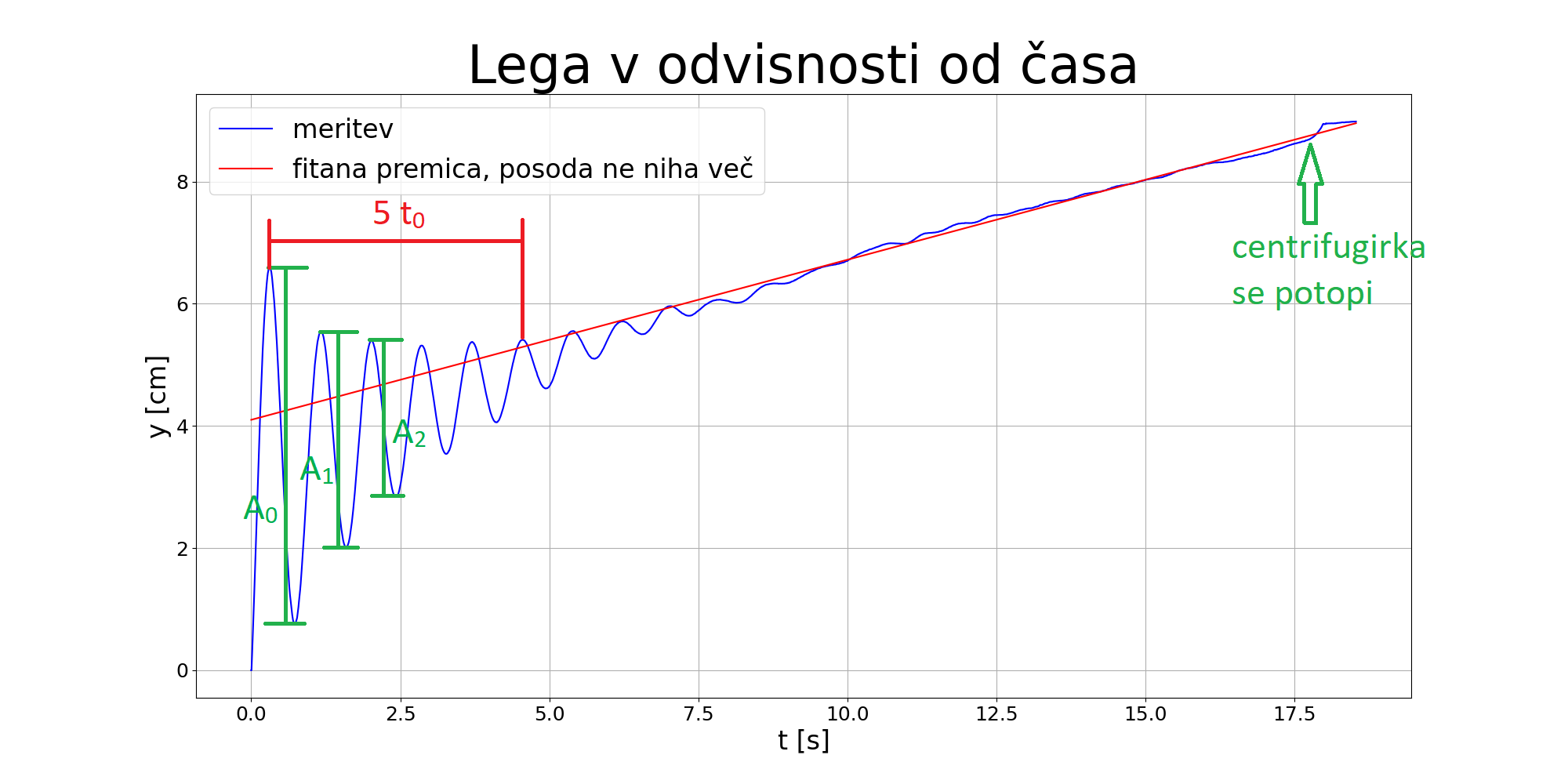
Na grafu 4 vidimo, da je lega gladine glede na centrifugirko, ko ta ne niha, sorazmerna s časom. Opazimo, da je graf nekoliko konkaven. Torej se hitrost potapljanja centrifugirke s časom zmanjša. Eden izmed vzrokov za to je morda oblika centrifugirke. Centrifugirka izgleda valjasta, vendar je polmer na spodnjem delu nekoliko manjši kot višje zgoraj. Tako se mora z vodo napolniti vse večji volumen pri potopu za isto globino. Sumimo, da ima na obliko grafa morda vpliv tudi združevanje dveh centrifugirk, saj se z združitvijo dveh centrifugirk zoža zgornji del spodnje centrifugirke in spodnji del zgornje centrifugirke.
Na koncu vseh grafov, po sedemnajstih sekundah, opazimo povečano hitrost. Preden je centrifugirko prekrila voda, je bil ob robu posode dobro opazen vpliv površinske napetosti vode. Ko pa je centrifugirka približno 3 mm pod gladino vode, voda od zgoraj steče v centrifugirko in zapolni preostali prazni volumen. Zaradi ohranitve gibalne količine se posoda z vodo začne gibati hitreje in nato v celoti potone. Čisto na koncu pa vidimo, da se posoda ne potaplja več, saj je zadela ob dno našega akvarija.
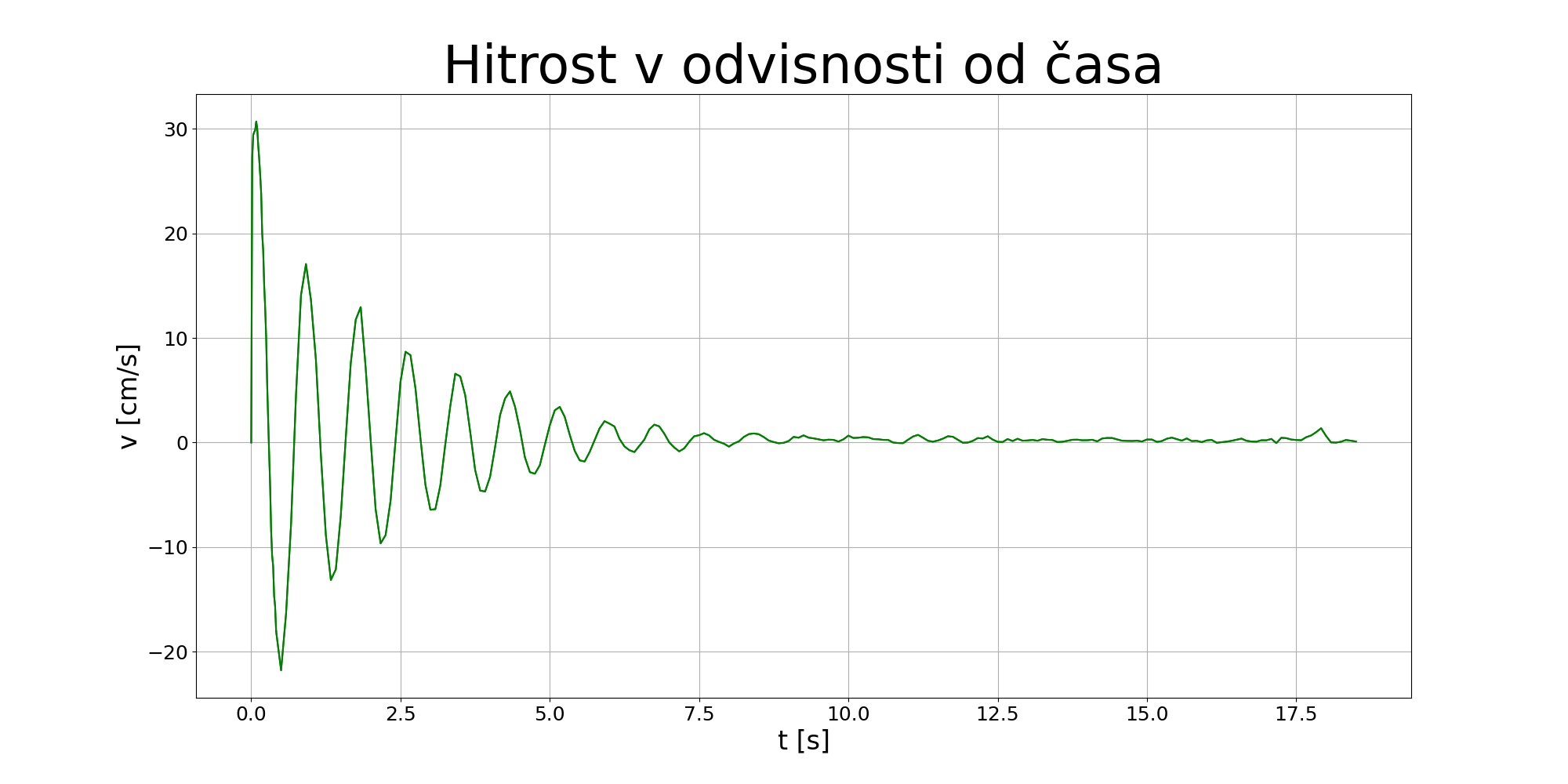
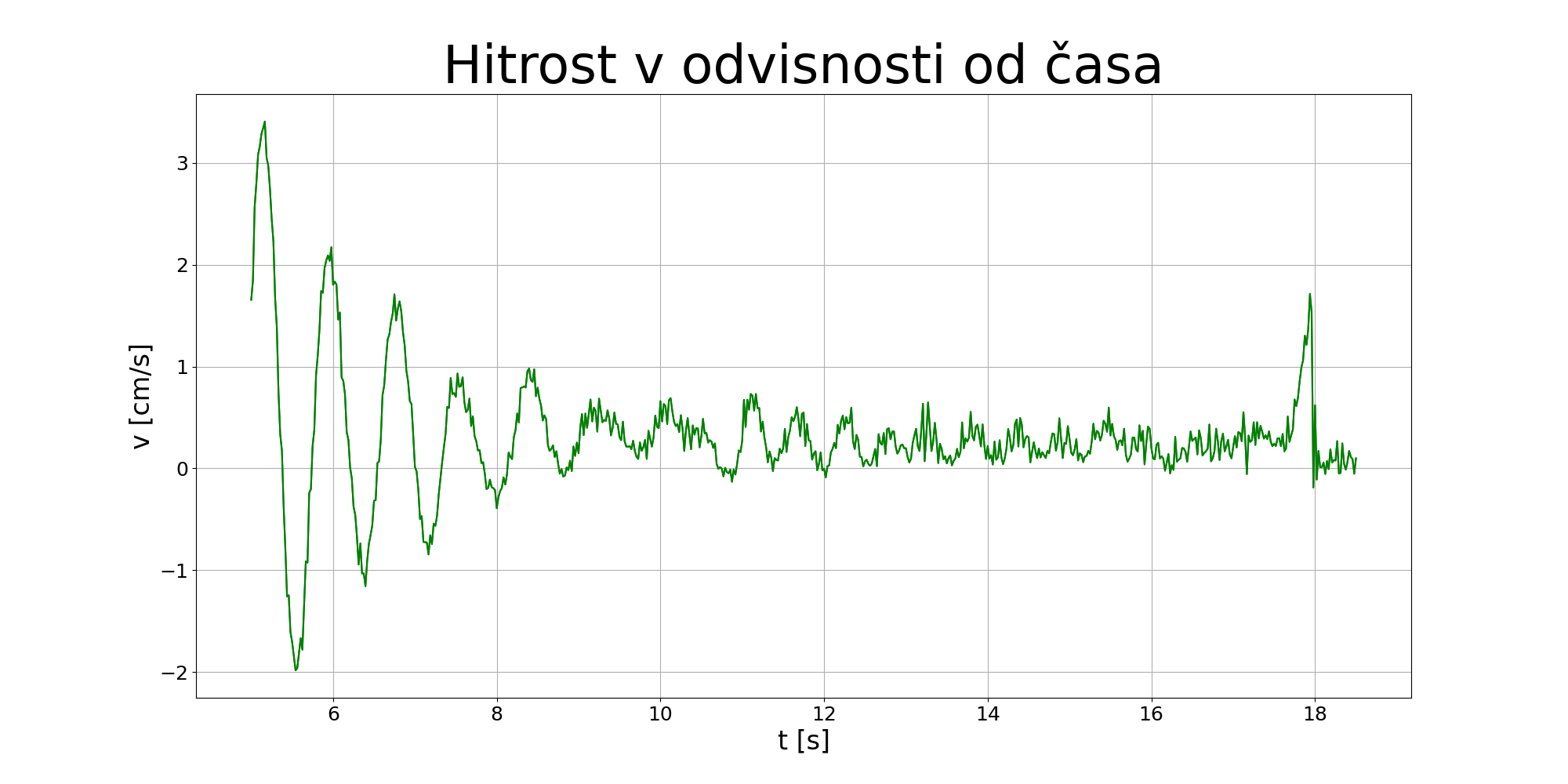
Na povečanem grafu hitrosti opazimo, da centrifugirka tudi proti koncu gibanja še vedno niha, vendar je po nekaj nihajih amplituda približno 0.01 začetne amplitude.
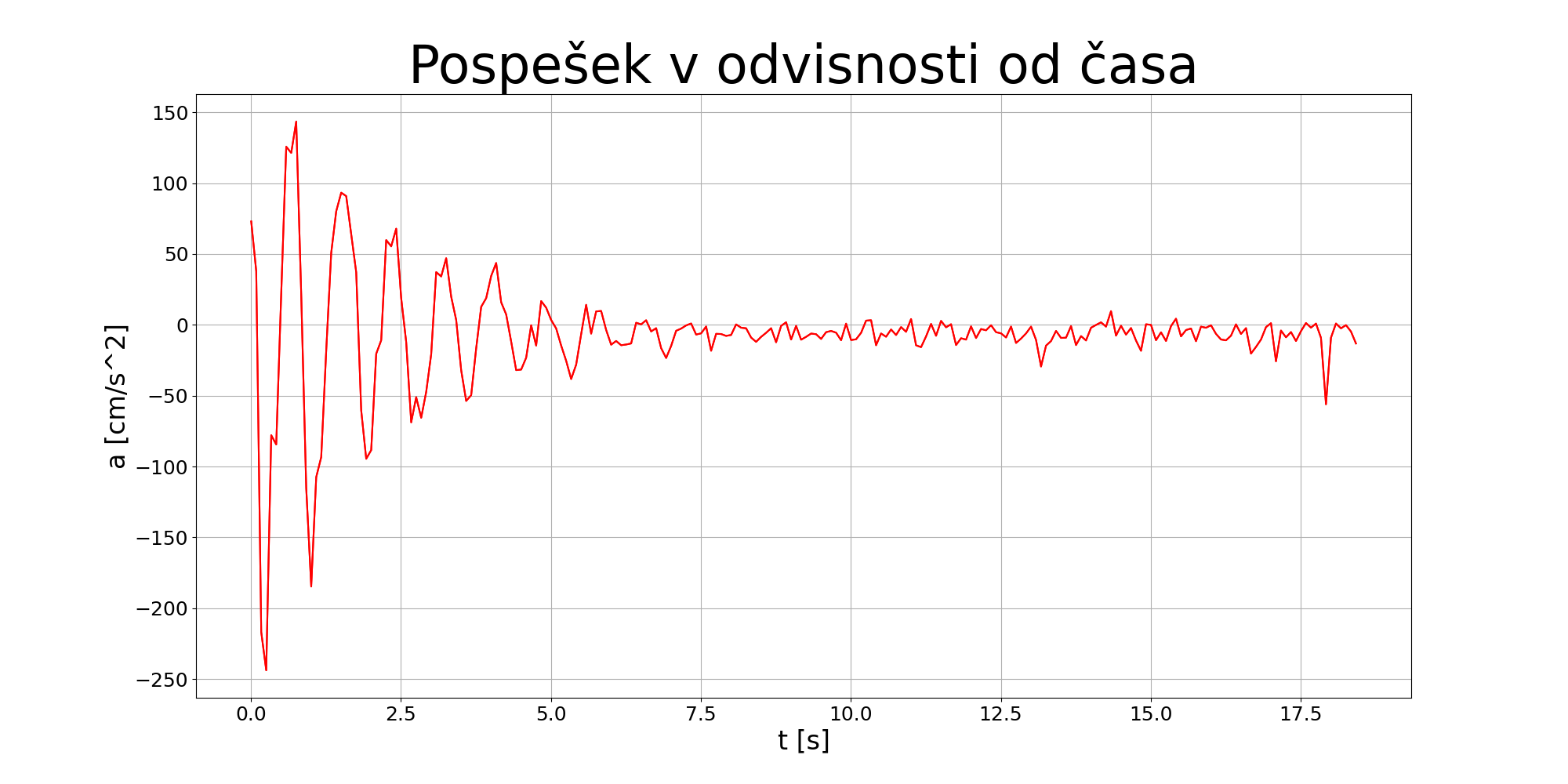
Po 5 sekundah lahko na grafu pospeška v odvisnosti od časa opazimo, da je pospešek večino časa negativen. To razloži konveksno obliko grafa lege v odvisnosti od časa. Prvih 5 sekund pa pospešek opazno niha. Iz premice na grafu lege v odvisnosti od časa pa ugotovimo, da povprečna hitrost na začetku pada.
Nihanje posode
Iz meritev smo za različne ponovitve poskusa odčitali nihajne čase in koeficiente dušenja nihanja posodice, ki ga opazimo na začetku potapljanja. V nadaljevanju razložimo, kako smo se tega lotili in omenimo dva opažena vzorca spreminjanja nihajnega časa in koeficienta dušenja v odvisnosti od naših parametrov (masa posode, število lukenj itd.). Tabela z vrednostmi t0 in β za več ponovitev poskusa se nahaja tule.
Nihajni čas
Nihajni čas je konstanten. Zaporedne ekstreme krivulje z[t] poiščemo s funkcijo FindPeaks v Mathematici. Če čase zaporednih ekstremov narišemo na grafe, ti kažejo izrazito linearno odvisnost (nihajni časi se ne spreminjajo vidno). Nihajni čas za vzorčni primer je 0,85 s ± 0,02 s.
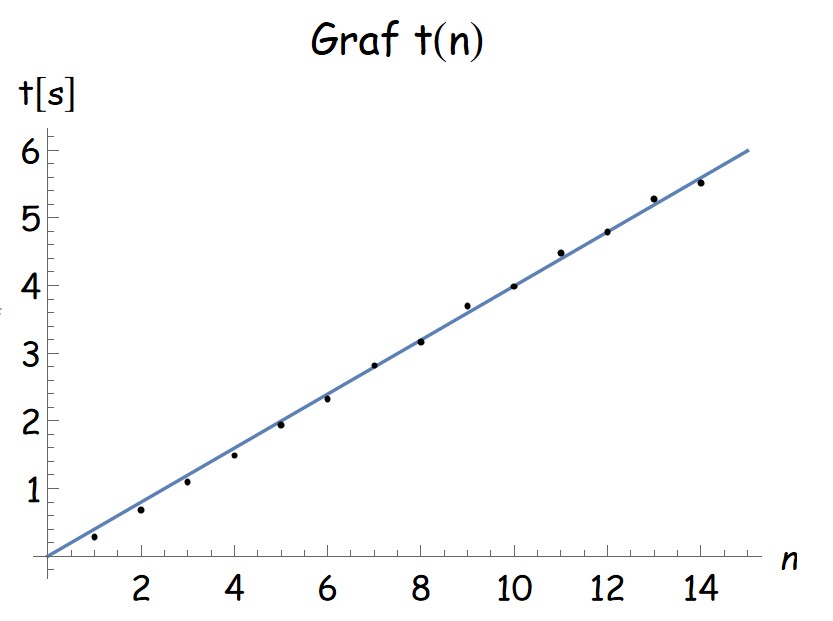
Nihajni čas posodic je pri posameznem poskusu konstanten. Pri različnih ponovitvah pa smo opazili, da se z večanjem mase posodice nekoliko poveča tudi nihajni čas. Pri odvisnosti nihajnega časa od ostalih parametrov nismo opazili jasnih vzorcev.
Koeficient dušenja
Za običajno linearno dušeno nihanje velja
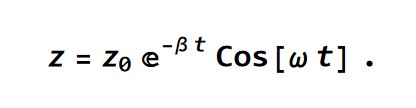
Razmerje sosednjih amplitud je torej
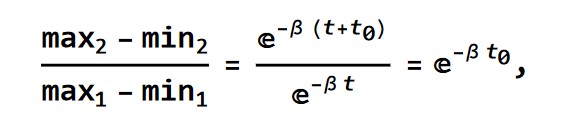
n-ta amplituda je tako
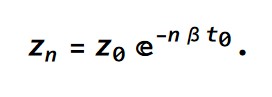
Če nihanje, "naloženo" na potapljanje, opišemo s tem modelom, dobimo dobro ujemanje (grafa 9 in 10).
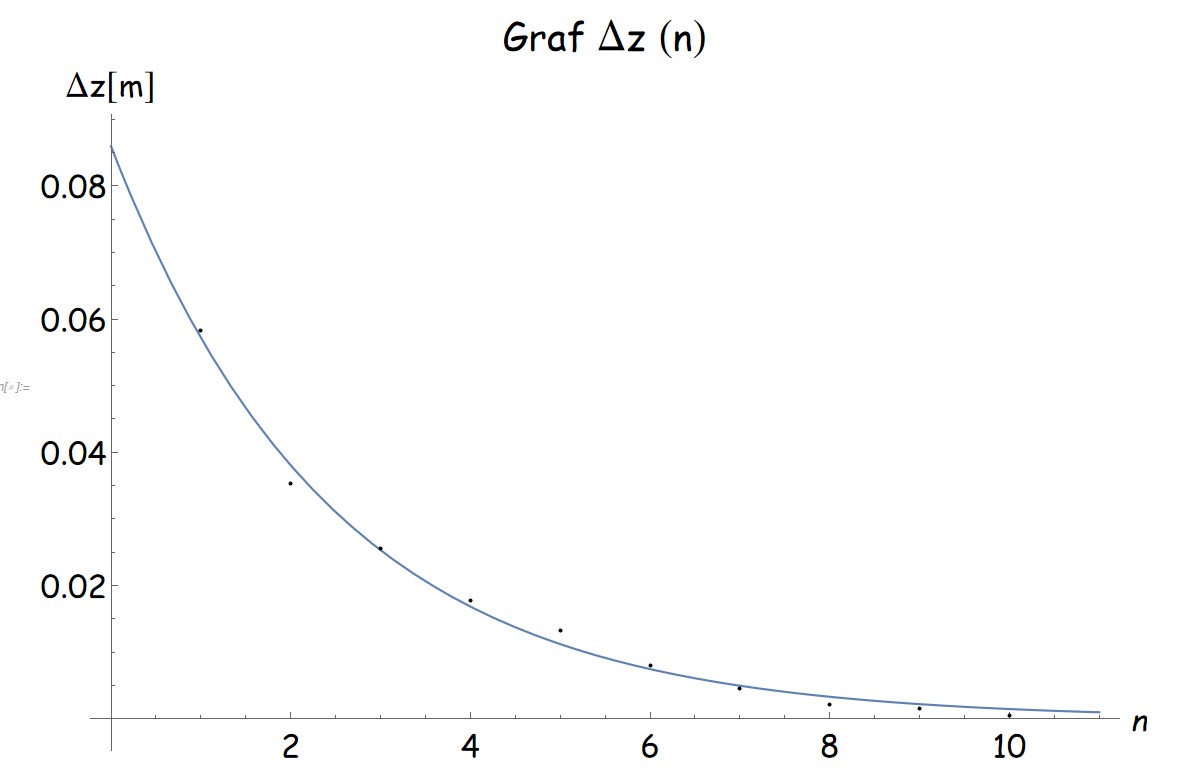
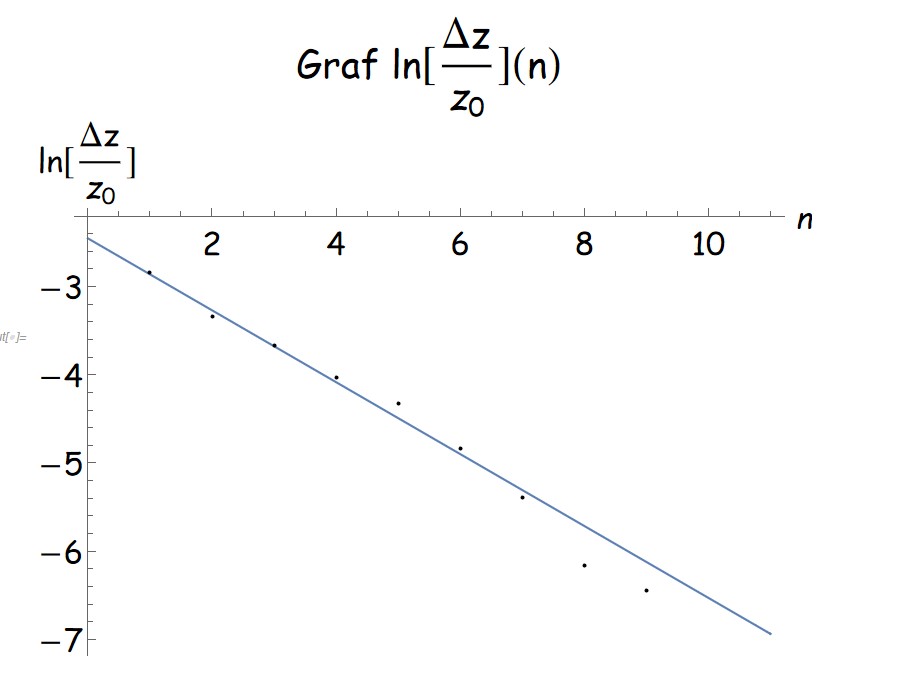
Za vzorčni primer je koeficient dušenja: 𝜷 = 0,46 s-1 ± 0,01 s-1. Pri preverjanju odvisnosti koeficienta dušenja od preiskovanih parametrov smo opazili, da se z večanjem števila lukenj koeficient povečuje. Pri ostalih parametrih ni jasnega vzorca.
Vpliv mase na čas potapljanja
Pri opazovanju vpliva mase na čas potapljanja, so bili ostali parametri konstantni. Centrifugirka je imela 2 luknji na steni posode s premerom 2,35 mm. Začetna masa je bila 28 g. Na magnet smo nato dodajali 4-gramske uteži.
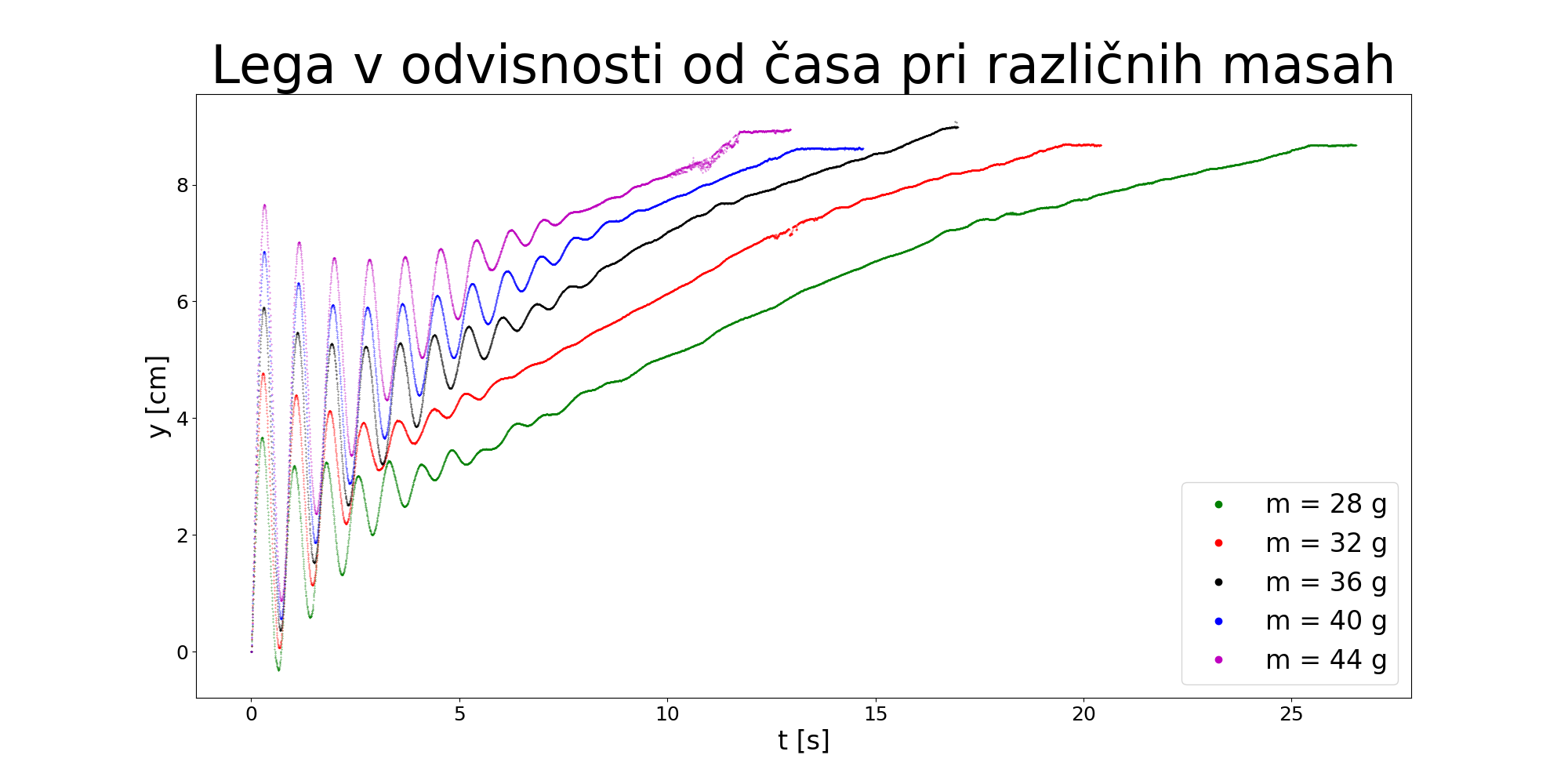
Čas potapljanja je obratno sorazmeren masi centrifugirke, torej se pri večji masi posoda potopi v krajšem času. Pri večji masi opazimo tudi večje amplitude nihanja in večjo poglobljenost na začetku. Zaradi večje mase je potreben večji vzgon, zato se posoda na začetku bolj potopi.
Graf časa potapljanja v odvisnosti od mase težko fitamo, saj imamo samo 5 podatkov, ki so po velikosti precej blizu. Tudi če bi imeli več meritev, nam verjetno ne bi uspelo primerno fitati grafa. Pri masah, ki so manjše od 28 g, je centrifugirka nestabilna in se prevrne. Pri masah, ki so še nekoliko večje od 44 g, pa se centrifugirka potopi v prvem nihaju. V primeru, ko je gostota centrifugirke in uteži manjša od gostote vode, se posoda ne bi potopila in bi bil čas potapljanja neskončen. Mejno maso za potop bi lahko izmerili tako, da bi dodajali uteži dokler se posoda ne bi potopila. Masa, pri kateri posoda lebdi, je mejna. Na to smo med načrtovanjem in izvajanjem poskusov, žal, pozabili. Funkcija, ki opiše odvisnost časa potapljanja od mase je gotovo definirana pri masah, pri katerih se posoda potopi. Funkcija ima dve asimptoti. Ena asimptota je navpična in leži na robu definicijskega območja, pri najmanjši masi, ko se posoda še potopi. Druga asimptota je vodoravna in je pri času potapljanja, ki je enak času prostega pada, saj posoda ne more hitreje potoniti.
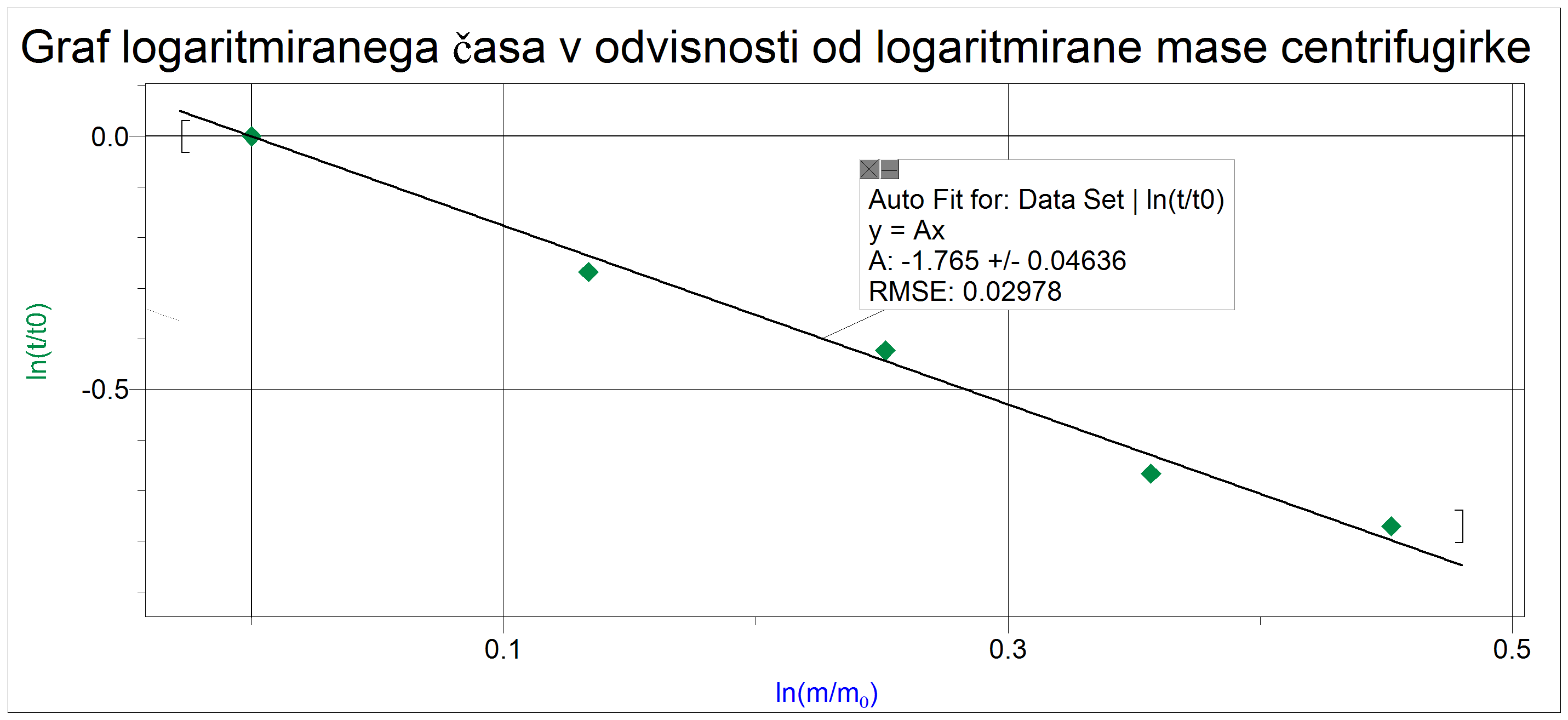
.png)
Iz logaritmiranega grafa opazimo, da se fitana premica zelo dobro prilagaja meritvam. Zgornjim pogojem gotovo ustrezajo funkcije t(m) = C / (m - m’)n + t0, pri čemer je m’ minimalna masa, pri kateri posoda še potone, t0 pa je čas prostega pada posode za isto višino. t0 je v našem primeru približno 0,04 s, m’ pa bi bilo potrebno izmeriti. V našem primeru je t0 zanemarljivo majhen, saj potapljanje vedno traja vsaj nekaj sekund. C je lastnost posode. Izmerimo jo lahko z eno meritvijo mase in časa potapljanja posode. Verjetno velja
C = T * (M - m’), kjer je T čas potapljanja posode, M pa masa posode.
Poleg centrifugirk smo spremljali tudi obnašanje pločevink pri različnih masah. Teh meritev nismo snemali s kamero, ampak smo samo merili čas potapljanja s štoparico. Merili smo čas potapljanja pri masah 42 g, 78 g, 102 g, 126 g in 162 g. Meritev vsake mase smo ponovili 3-krat. Meritve so precej natančne, saj je največja negotovost za posamezno maso 0,3 s.
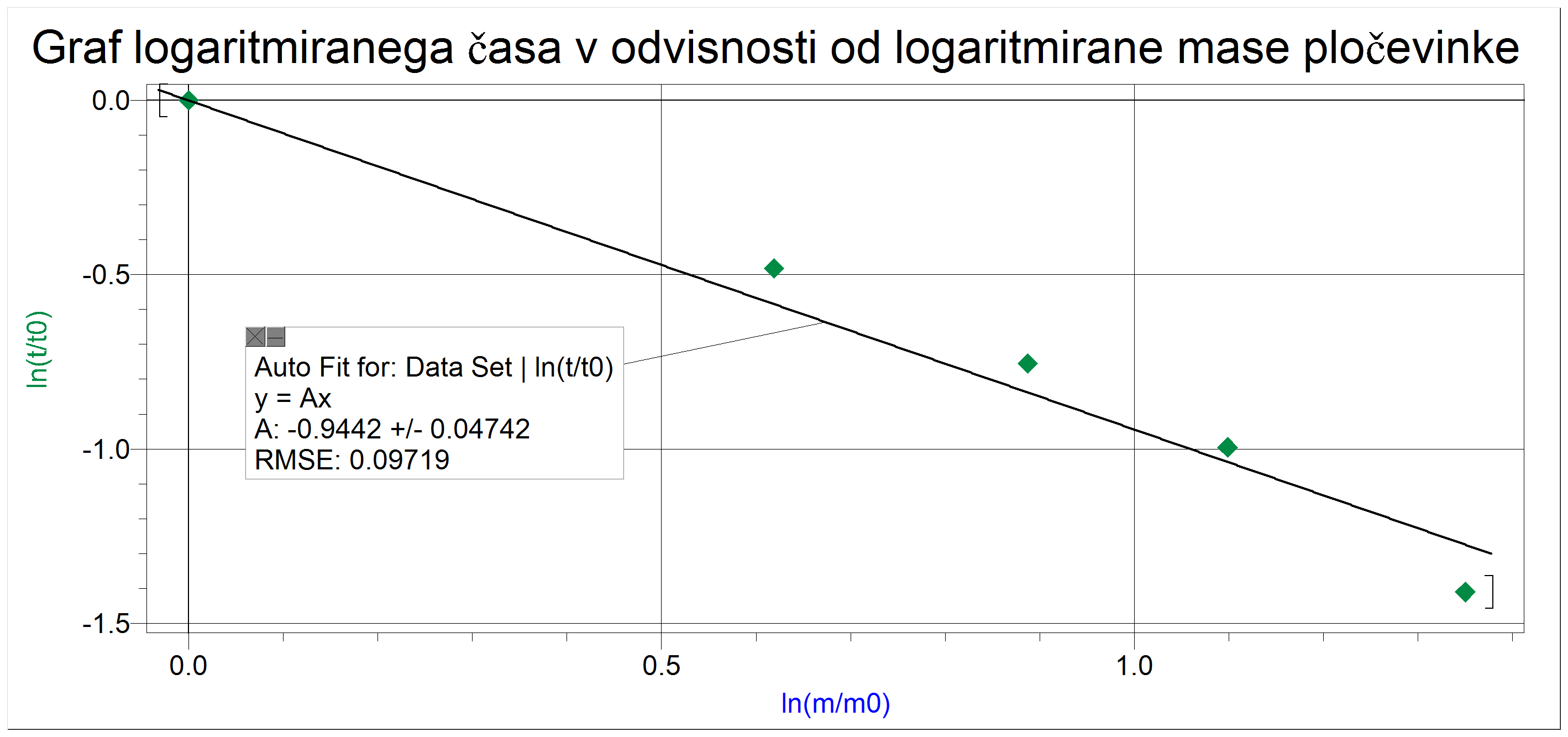
Grafa mase v odvisnosti od časa za pločevinko in centrifugirko izgledata podobno, čeprav sta posodi popolnoma različni. Tudi logaritmiran graf spominja na premico, vendar so podatki nekoliko bolj razpršeni. Graf pločevinke ima malo večji razpon meritev, zato je bolj primeren za fitanje. Pričakovana funkcija t(m) je podobna funkciji pri centrifugirki. V tem primeru ni mejne mase, saj je posoda že brez dodatnih uteži gostejša od vode.
.png)
Vpliv velikosti lukenj na čas potapljanja

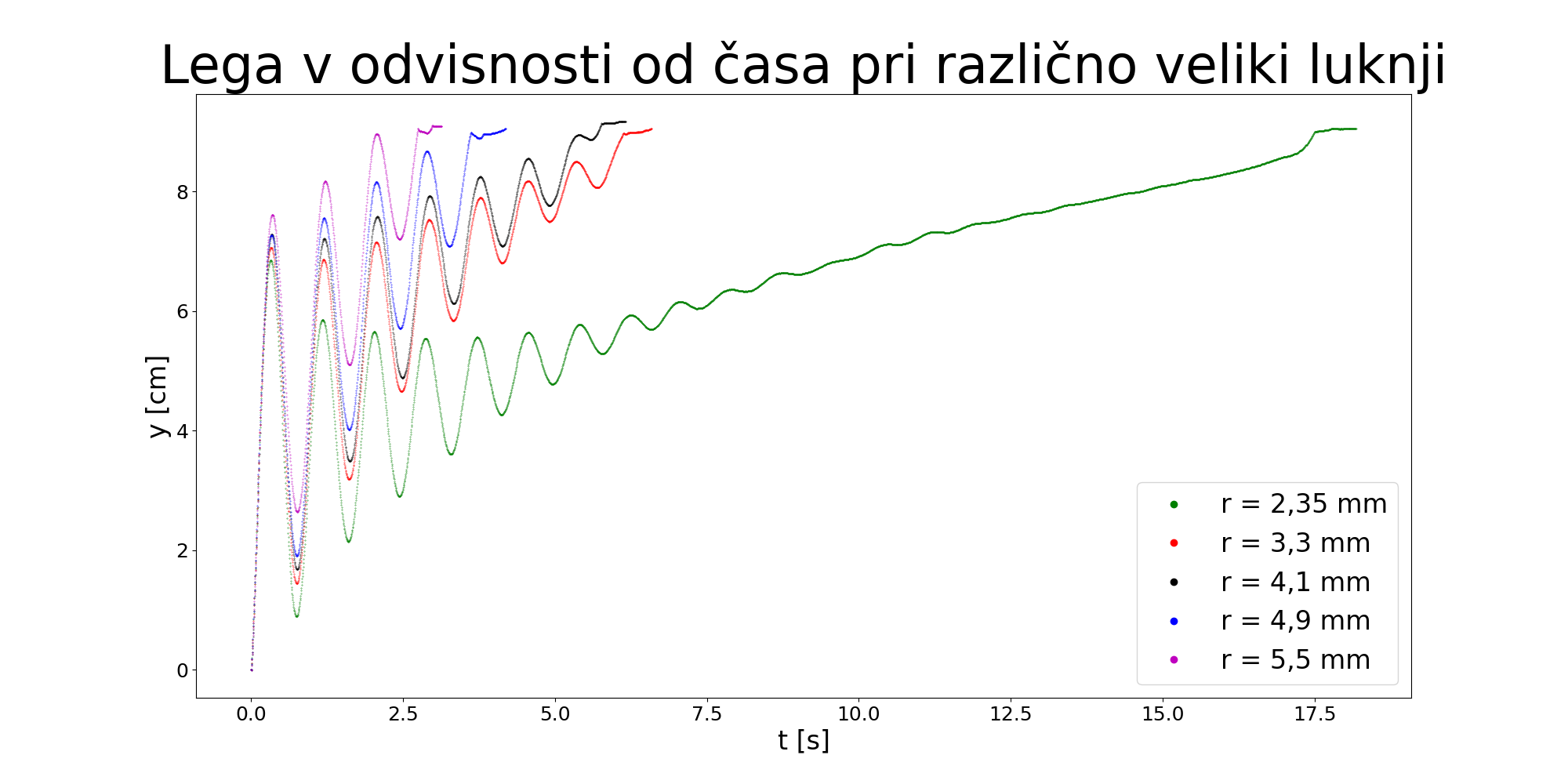
Pri opazovanju vpliva velikosti lukenj na čas potapljanja so bili ostali parametri konstantni. Centrifugirka je imela maso 32 gramov in ima eno luknjo na dnu posode. Menjali smo spodnji del spojke centrifugirk tako, da je bil premer luknje vsakič drugačen. Luknje so imele premere 2.35 mm, 3.3 mm, 4.1 mm, 4.9 mm, 5.5 mm.
Izračunali smo preseke lukenj in njihove pripadajoče relativne napake, kar je prikazano v tabeli.
Kot je razloženo v poglavju o merskih negotovostih, je napaka sestavljena iz 0,05 mm napake meritve svedra, 2 % zaradi nenatančnega vrtalnika ter 1 % zaradi stopljene plastike.
Iz grafa lege v odvisnosti od časa lahko očitamo čas potapljanja. Čas odčitamo ročno, najlažje s pomočjo orodja, ki meri razdalje na sliki. Če na graf nanesemo čas potapljanja v odvisnosti od preseka luknje dobimo obliko ki spominja po obliki na funkcijo 1/x. Zato izračunamo povprečno hitrost potapljanja ter to vstavimo v graf v odvisnosti od preseka luknje.
| Premer [mm] | Presek [mm2] | Relativna negotovost preseka [%] | Čas potapljanja [s] | Povprečna hitrost potapljanja [cm/s] |
|---|---|---|---|---|
| 2,35 | 4,3 | 7 | 17,5 | 0,51 |
| 3,3 | 8,5 | 6 | 6,14 | 1,5 |
| 4,1 | 13 | 5 | 5,77 | 1,6 |
| 4,9 | 19 | 5 | 3,61 | 2,5 |
| 5,5 | 24 | 5 | 2,76 | 3,3 |
Preko točk na grafu s pomočjo paralelograma narišemo premico, saj je po modelu čas potapljanja premo sorazmeren s presekom luknje. Funkcija najbolje prilegajoče se premice je
Napaka te funkcije je 20%, ta funkcija je uporabna zgolj na območju med največjim in najmanjšim preizkušenim presekom. Pri manjših luknjah je namreč treba upoštevati še kapilarni efekt ter viskoznost tekočine, pri večjih luknjah pa kmalu pridemo do preseka primerljivega s presekom posode, kar pa bi bil kar prosti pad posode brez dna v tekočini.
Vpliv števila lukenj na čas potapljanja

Pri opazovanju vpliva števila lukenj na čas potapljanja, so bili ostali parametri konstantni. Centrifugirka je imela maso 32 gramov in ima dve luknji na steni posode. Menjali smo spodnji del spojke centrifugirk, tako da je bilo število lukenj vsakič drugačno. Število lukenj se je spreminjalo: 1, 2, 3, 4, 6, 8, 12.
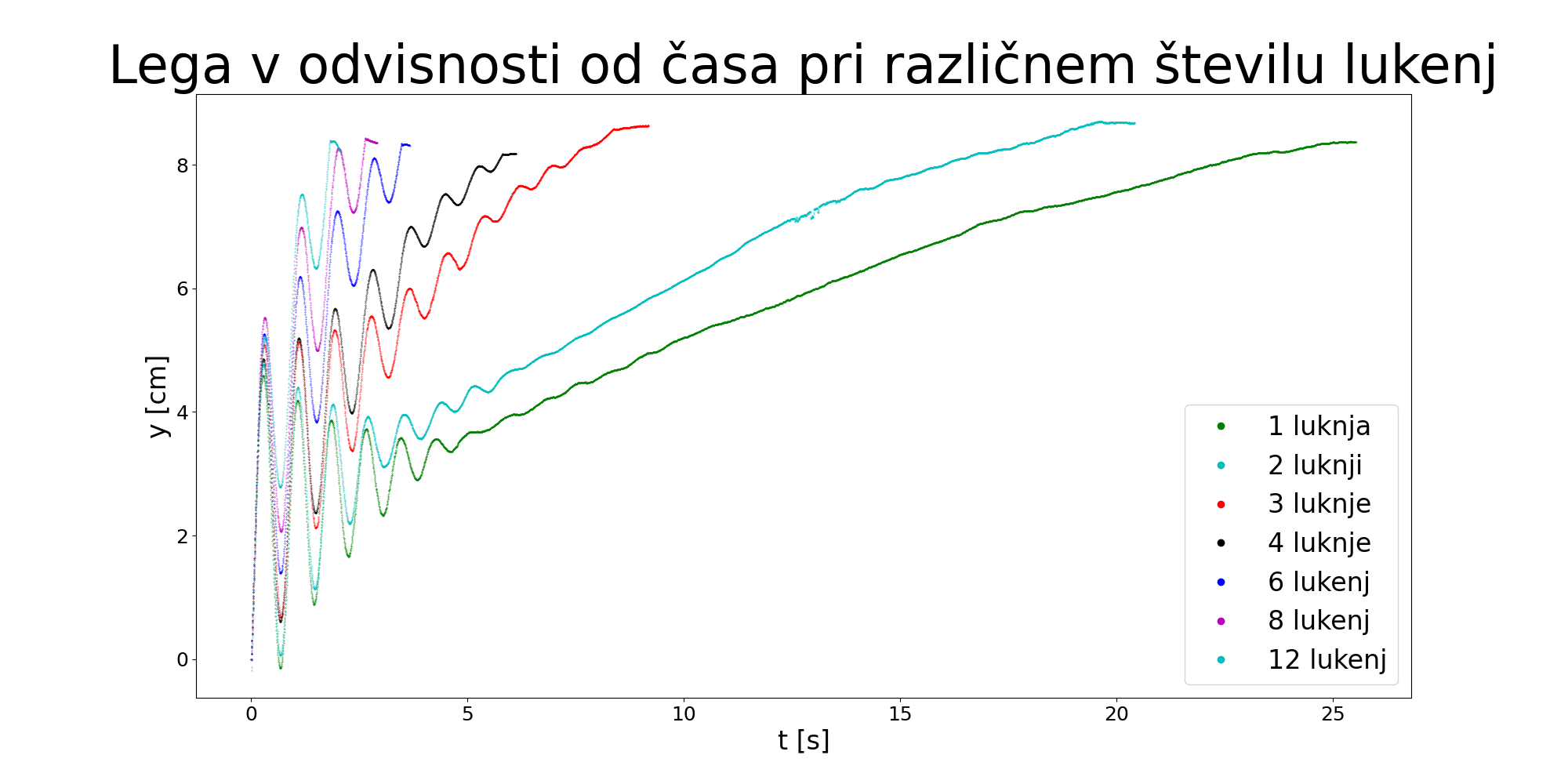
Kot je opisano v poglavju o negotovosti meritev, imamo premer svedra za vrtanje luknje določen na 0,05 mm natančno. To pri 2,35mm premera svedra pomeni 2% napake. Ko iz tega izračunamo presek luknje je to 4%, ter dodatne 4% zaradi nepravilnosti vrtanja, kar nam da 8% napake.
Iz grafa lahko očitamo čas potapljanja. Čas odčitamo ročno, najlažje s pomočjo orodja ki meri razdalje na sliki. Če na graf nanesemo čas potapljanja v odvisnosti od preseka luknje dobimo obliko ki spominja po obliki na funkcijo 1/x. Zato izračunamo povprečno hitrost potapljanja ter to vstavimo v graf v odvisnosti od števila lukenj.
Z enako metodo kot pri prejšnjem poglavju narišemo graf povprečne hitrosti potapljanja v odvisnosti od skupne površine vseh lukenj.
Preko točk na grafu s pomočjo paralelograma narišem premico, saj je po modelu čas potapljanja linearno sorazmeren s skupnim presekom lukenj. Funkcija najbolje prilegajoče se premice je
Območje natančnosti te funkcije je vsekakor za manj kot 12 lukenj, lahko bi bilo še za več, vendar tega z eksperimentom v tej obliki ne moremo preveriti. Namreč, če bi naredili nekaj več kot 12 lukenj, bi se bodisi luknje začele dotikati, kar pomeni da načeloma ni več lukenj, ampak nekaj večjih, ali pa bi bilo potrebno narediti luknje na različnih višinah. Če bi imeli toliko lukenj da bi jih bilo potrebno dati na različne višine, bi prišlo do dodatnih netočnosti ter napak, za več podatkov glej analizo odvisnosti časa potapljanja od višine luknje.
Primerjava pri enaki površini lukenj
Primerjali smo čas potapljanja pri podobni skupni površini lukenj. V enem primeru smo imeli 1 luknjo s premerom 4,9 mm; v drugem primeru pa smo imeli 4 luknje s premerom 2,4 mm. Ostali parametri so v obeh primerih enaki.
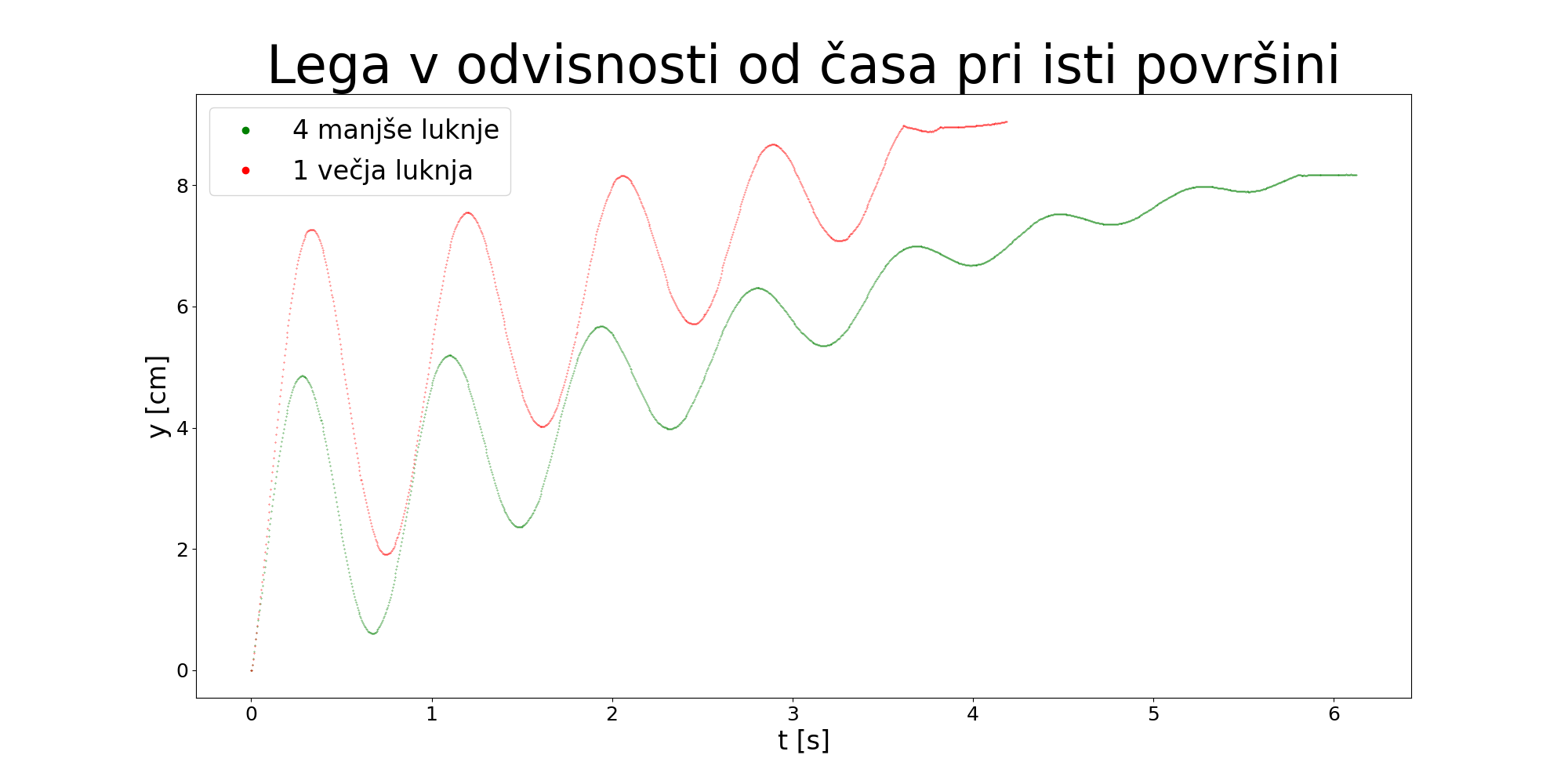
Iz grafa lahko odčitamo, da se posoda z eno večjo luknjo potaplja približno 3,5 s, posoda s 4 manjšimi pa približno 6 s. Razlike je približno za faktor 1,7. Sicer so luknje pri meritvah na različnih višinah, vendar v naslednjem poglavju ugotovimo, da lahko to spremeni rezultate za manj kot faktor 1,03. Če temu dodamo še 8% napake smo še vedno komaj na faktorju 1,1, kar pomeni da mora obstajati fizikalni razlog, da sta si časa tako različna. Naša teorija je, da takšno razliko dobimo zaradi enega ali obeh sledečih razlogov:
i. manjše luknje so dovolj majhne, da viskoznost vode ni več zanemarljiva, kar pomeni, da se ustvari kapilarni efekt, ki zavira pretok vode.
ii. pri večjih luknjah se ustvarijo turbulence, zaradi katerih teče voda hitreje, kot če je tok laminaren.
Če bi želeli ugotoviti kateri izmed razlogov je prevladujoč, bi bilo potrebno zasnovati več bolj kompliciranih eksperimentov, kot na primer opazovanje tokovnic, merjenje viskoznosti, in podobno. Za te eksperimente bi potrebovali nekaj napredne opreme, ki nam ni na voljo, ter mnogo več časa.
Vpliv višine lege luknje na čas potapljanja

Čas potapljanja pri različnih višinah lege lukenj smo merili s štoparico. Merili smo primerjalno, kar pomeni, da smo spuščali po dve posodici hkrati, ter merili čas. Ko sta bili luknji na obeh posodicah nižje, smo posodici prav tako spuščali z nižje višine. S tem smo zmanjšali relativno napako meritve, saj smo tako dosegli daljše meritve časov. To pomeni da je relativna napaka pri enaki absolutni napaki manjša. Višina spuščanja pa je v vseh primerih morala biti višje od najvišje luknje, saj sta morali biti obe luknji pod gladino vode, da lahko skozi njih teče voda. Za merjenje višine smo uporabljali narisane oznake, ki so pomenile volumen posode pod oznako.
V naslednji tabeli so zapisane razdalje oznak na centrifugirki od zgornjega roba:
| Oznaka | Razdalja do zgornjega roba [cm] |
|---|---|
| 5 ml | 5,06 |
| 10 ml | 5,91 |
| 15 ml | 6,83 |
| 20 ml | 7,73 |
| 25 ml | 8,65 |
| 30 ml | 9,60 |
Pare lukenj 5, 10, 15 ml smo spuščali z gladine pri oznaki 20 ml.
V tabeli so podani povprečni časi potapljanja z dane višine za vsak par. Vsak par posodic smo spustili 6-krat.
| Lega luknje | Povprečni čas potapljanja [s] |
|---|---|
| 5 ml | 19,47 |
| 10 ml | 19,23 |
| Lega luknje | Povprečni čas potapljanja [s] |
|---|---|
| 5 ml | 19,67 |
| 15 ml | 17,39 |
| Lega luknje | Povprečni čas potapljanja [s] |
|---|---|
| 10 ml | 18,99 |
| 15 ml | 17,64 |
Pri parih z eno od lukenj pri oznaki 25 ml smo spuščali centrifugirke z višine pri oznaki 30 ml. Pri paru 15 ml in 25 ml smo poskus ponovili 12-krat, pri paru 5 ml in 25 ml pa 3-krat.
| Lega luknje | Povprečni čas potapljanja [s] |
|---|---|
| 15 ml | 12,69 |
| 25 ml | 12,65 |
| Lega luknje | Povprečni čas potapljanja [s] |
|---|---|
| 5 ml | 14,42 |
| 25 ml | 12,35 |
Pri danih meritvah je jasno, da je čas potapljanja odvisen od višine na kateri se nahaja luknja. Največja razlika je med posodicama z luknjama pri oznakah 5 ml in 25 ml. Odstopanje enega časa od drugega je približno 15%, kar je več kot znaša merska napaka (2% površina luknje + 2% spuščanje iz različne višine + 2% napaka štopanja = 6%). Če želimo izračunati odvisnost, je potrebno opraviti nekaj več izračunov.
Želimo primerjati meritve pri spuščanju iz višin pri 20 ml ter pri 30 ml. Teh meritev ne moremo primerjati neposredno, saj centrifugirke, ki so bile na začetku bolj potopljene prepotujejo manjšo pot, kar pomeni da se bodo hitreje potopile, ne glede na lego luknje. Zato moramo čase primerjat s časi pri višinah, ki so bile uporabljene v obeh primerih. Tako lahko primerjamo bodisi z luknjo pri oznaki 5 ml ali pa pri oznaki 15 ml.
Tako torej, ko primerjamo s časom pri 5 ml, delimo dobljene čase pri luknjah pri danih višinah s časom izmerjenim pri luknji na 5 ml.
Ko imamo za dano višino več časov, vzamemo tistega, ki je bil izmerjen hkrati s primerjalno višino. To pomeni, da za tabelo primerjanja s posodico z luknjo pri oznaki 5 ml vzamemo meritve, ki so bile merjene v paru s posodico z luknjo pri 5 ml. S ponavljanjem meritev smo zmanjšali napako merjenja časa zaradi slučajne napake pri merjenju časa. Napaki zaradi nepravilnosti pri vrtanju lukenj se z večkrat ponovljeno meritvijo ne moremo izogniti. Če bi želeli zmanjšati to napako, bi bilo potrebno narediti več posodic z luknjo na neki dani višini.
Absolutna napaka meritve časa je 0,1 s, kar pri meritvah časov nad 12 s pomeni približno 0,8 % relativne napake. Ker smo meritve ponavljali po šestkrat, lahko napako delimo s korenom 6, kar nam da relativno napako 0,3 %. Relativna napaka polmera luknje je 2 %. To nam da 4 % relativne napake površine luknje. Temu dodamo še 2% napake kot je obrazloženo v poglavju o negotovostih meritev. Tako dobimo napako površine luknje 6 %, pri čemer je napaka meritve časa zanemarljiva.
Tako lahko izmerjene podatke tolmačimo kot trend, in ne kot zgolj napako pri merjenju/ izdelavi lukenj, kar pomeni, da je čas spuščanja odvisen od višine pri kateri je izvrtana luknja.
Iz naklona premice izračunamo koliko napake pridelamo zaradi spremembe višine luknje. Pri meritvah v primerjavi z posodico z luknjo pri 5 ml dobimo 4% na razdaljo med dvema oznakama, pri meritvah v primerjavi s posodico z luknjo pri 15ml pa 3%. Ko to preračunamo v cm dobimo v povprečju 3% napake na cm. Ta podatek nam pride prav pri primerjavi časov potapljanja pri eni ali več luknjah z isto površino. Zaradi narave posode smo namreč v različnih poglavjih raziskave vrtali luknje na različnih lokacijah, znotraj poglavja pa na isti (izjema je to poglavje).
Razlog za odvisnost od višine luknje bi lahko bilo to, da posoda ni valjasta. Izmerili smo namreč, da se zunanji premer posode spreminja z višino, vendar nam bi bolj prav prišel podatek notranjega polmera v odvisnosti od višine. Tega pa z našo opremo ni bilo mogoče izmeriti.