SAŠKA URA

Najosnovnejši teoretični model

Uvod

Za gibanje posodice bomo uporabili 2. Newtonov zakon (F = m a) in Bernoullijevo enačbo.

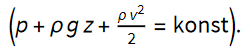
Posodico z utežmi, magnetki in vodo v njej obravnavamo kot sistem (vedno, ko bo omenjen sistem, bo mišljen ta sistem). Pospešek težišča sistema bosta v vsakem trenutku določali njegova masa v tem trenutku in sile nanj (F = m a). Sili, ki na ta sistem delujeta, sta teža sistema in sila vode nanj. F vode bomo še podrobneje razdelali (vzgona, curka, upora). Če znamo določiti gibanje težišča sistema in vode v posodici, lahko določimo tudi gibanje posodice.

Predpostavke modela

Za naš model predpostavimo naslednje:

1. Posodica se giba samo v navpični smeri.
2. Posodica je vedno pokončno obrnjena vrtenina.
3. Višina zunanje gladine se ne spreminja (akvarij je volumski rezervoar na višini 0).
4. Luknje so v primerjavi z dimenzijami posodice blizu njenega dna. (Ta predpostavka je vezana samo na idealizacijo uporabljenih centrifugirk (kako jih upoštevamo v splošnejšem modelu))
5. Prostornini stožca na dnu posodice in magnetov v njej sta zanemarljivi v primerjavi s celotno prostornino vode v posodici. Njuna razlika, ki bi sicer nastopala v nekaterih enačbah, je še zanemarljivejša.
6. Zanemarimo površinsko napetost vode.
7. Uporabimo Bernoullijevo enačbo, pri čemer zanemarimo viskoznost vode.
8. Sila upora na sistem je taka, da je pospešek zaradi nje približno sorazmeren s hitrostjo posodice.

Oznake

Preden začnemo s podrobnejšo razlago, lahko naštejemo nekaj oznak, ki jih bomo pogosto uporabljali:

Indeksi:

• p za posodico (npr. v_p je hitrost posodice)
• c za curek vode skozi luknje v posodi
• l za luknje
• ng za notranjo gladino
• rel za glede na posodico (*sicer vse v sistemu zunanje gladine*)

Običajne oznake:

• N za števila
• S za ploščine
• z za navpično koordinato, glede na zunanjo gladino, merjeno navzgor (kjer piše lega, je mišljeno z-koordinata )
• v za hitrosti
• V za prostornine

Sicer uporabljamo običajne fizikalne oznake npr.: t za čes, R za polmer...

Tako na primer v_c,rel pomeni hirost curka vode, skozi luknje v posodici, glede na posodico.

Posebne oznake

• z_p=z_l lega lukenj posodice (To vzamemo za lego posodice.)
• R[z] polmer posodice na višini z od lukenj
• m_p masa posodice z magnetki in utežmi vred
• z_ng lega notranje gladine
• F_u sila upora
• V_izp prostornina izpodrinjene vode
• m_v masa vode v posodici

Teža sistema (m g)

Masa posodic z magneti in utežmi se v posameznem eksperimentu ne spreminja. Masa vode v posodici se spreminja sorazmerno masnemu pretoku skozi luknje.

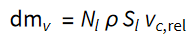
kjer je ρ gostota vode.

Začetna masa vode v posodici je sorazmerna z njeno začetno prostornino. Po 5. predpostavki lahko to prostornino izračunamo kot za vrtenino od lukenj navzgor:

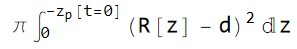
kjer je d debelina posodice. (Spomnimo se: za lego posodice z_p smo vzeli lego njenih lukenj).

Hitrost curkov skozi luknje

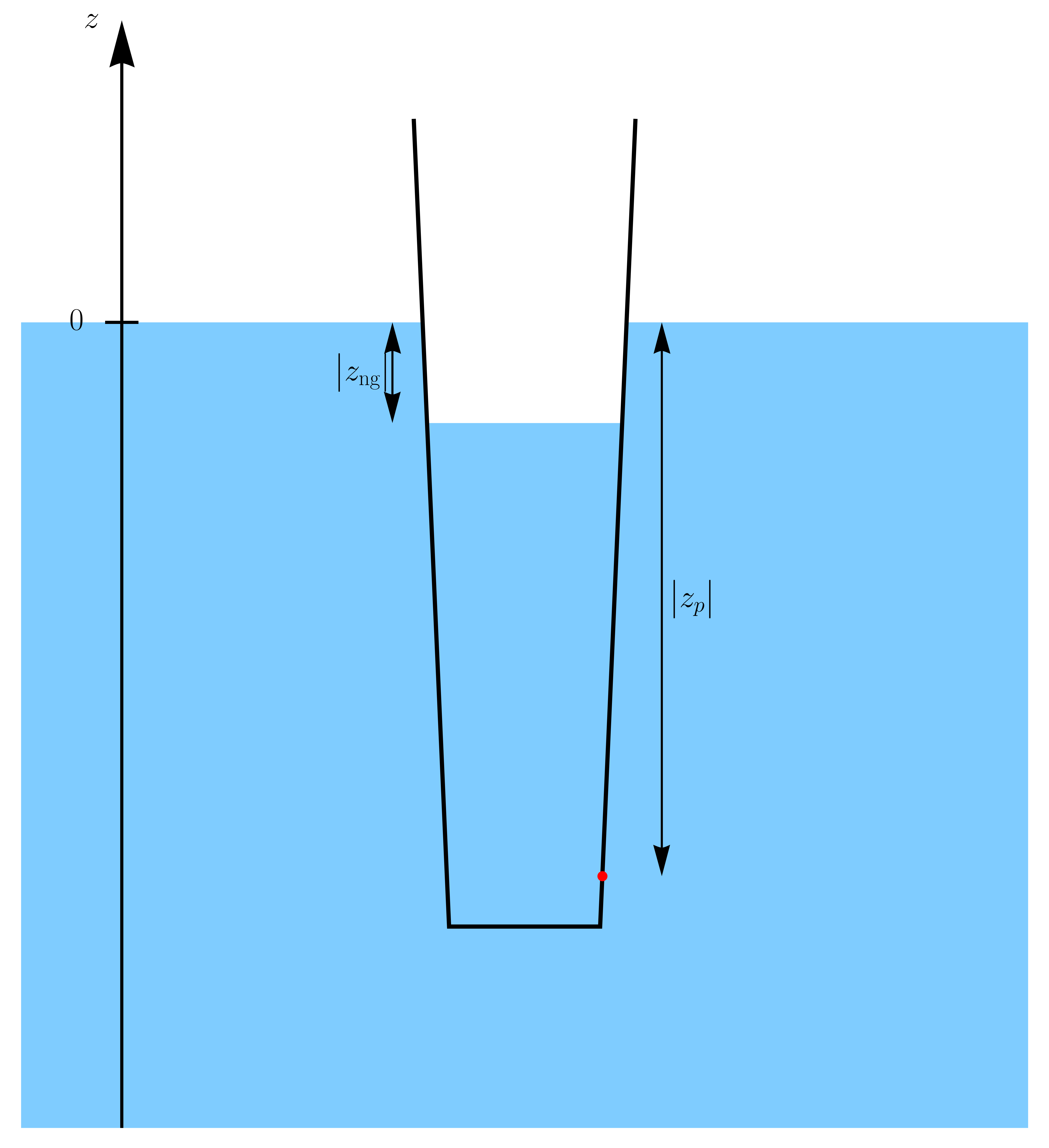
Hitrost curka bomo izračunali z Bernoullijevo enačbo. Leva in desna stran enačbe se nanašata na točki levo in desno od luknje. Pri tem bomo ničlo potencialne energije postavili na višino luknje.

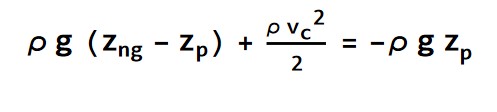
Iz Bernoullijeve enačbe izrazimo hitrost curka

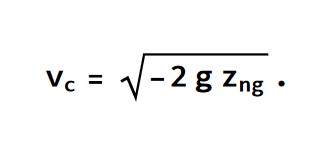
Leva stran enačbe je za točko pred luknjo posodice (na notranji strani posodice), desna pa za točko na zunanji gladini.

Hitrosti curkov so pri tipičnih vrednostih z_ng, to je nekaj cm, velikostnega reda 1 m/s, kar je za nekje 2 velikostna reda večje od hitrosti gibanja posodice (glej graf). Popravke hitrosti pretakanja vode zaradi gibanja posodice lahko torej zanemarimo.

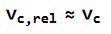
Sicer bi morali tudi različno obravnavati stranske in spodnje luknje.

Sila vzgona

Sila vzgona je nasprotna teži izpodrinjene vode.

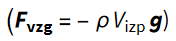
Za posodico to izračunamo z vrtenino, kot je bilo opisano zgoraj. Tudi spreminjanje te prostornine opišemo podobno, kot zgoraj:

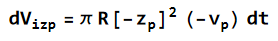
kjer je V_izp prostornina izpodrinjene vode.

Sila upora

Silo upora modeliramo tako, da opiše običajno linearno dušeno nihanje,

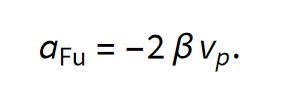
Sila dušenja na sistem je potem

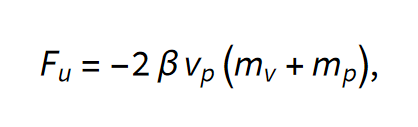
kjer je m_v masa vode v posodici.

Treba je opozoriti, da zadnja enačba za silo upora fizikalno nima nobenega smisla. Upor seveda ni odvisen od mase sistema, pač pa od geometrije potopljenega dela posodice. Vemo pa, da s časom (povprečeno na nihaj) naraščata tako masa posodice, kot tudi površina posodice na kateri deluje viskozno trenje. Gre torej za linearni približek funkcije

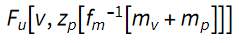
f_m je na interval nihajnega časa glajena funkcija mase sistema v odvisnosti od časa.

Gibanje

Po zakonu o gibalni količini za sistem velja

kjer zadnji člen dm_vv_c velja pri luknjah na dnu posodice, pri stranskih pa vzamemo navpično komponento hitrosti curka,

Do tega rezultata lahko pridemo tako, da vzamemo vektor, tangenten na plašč posodice. Tak je na primer vektor (R'[0], 1). Zavrtimo ga za 90° in dobimo (-1, R'[0]). Dobljen vektor je normala posodice in kaže v smeri curka. Če s to normalo izrazimo vektor v_c in vzamemo njegovo navpično komponento, dobimo prejšnji rezultat za v_{c, z}.

S tako opisanim spreminjanjem, lahko v vsakem trenutku izračunamo gibalno količino sistema.

Gibalno količino vode v posodici glede na posodico lahko izračunamo tako:

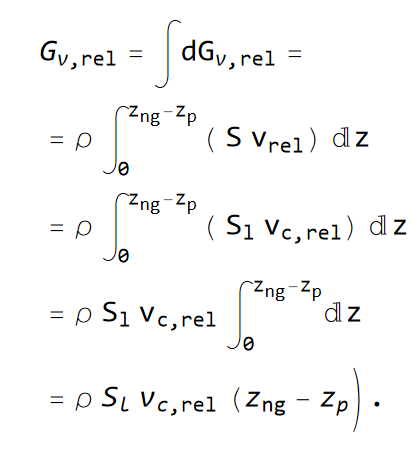
Gibalna količina vode v laboratorijskem koordinatnem sistemu je zato

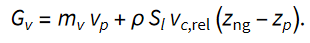
Tako lahko gibalno količino sistema izrazimo kot

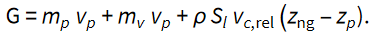
Od tod lahko izrazimo hitrost posodice

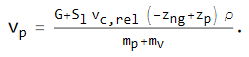
Na ta način torej lahko opišemo gibanje posodice.

Gibanje posodice dobimo itarativno, s fizikalno simulacijo. V vsakem kratkem časovnem koraku simulacije, dt izračunamo spremembo gibalne količine sistema dG. Iz posodobljene gibalne količine G po zadnji formuli izrazimo hitrost posodice v_p. Legi posodice naposled prištejemo njeno spremembo v_pdt. Uporaba Eulerjevega algoritma v tem primeru ni ovira, saj problem računsko ni zahteven in lahko računamo z zelo majhnim časovnim korakom dt.

Poenostavitev

V stacionarnem režimu, to je, ko se hitrost posodice ne spreminja več, se opis poenostavi. Vzeli bomo nekaj dodatnih predpostavk:

1. Posodice so valjaste
2. Stene posodic nimajo debeline
3. Uporne sile so zanemarljive

Ob predpostavki III mora v stacionarnem režimu vzgon uravnovešati težo sistema

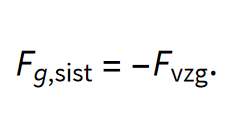
Od tod dobimo

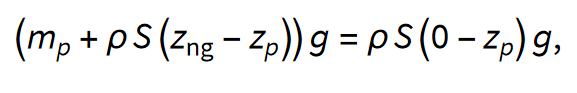
iz česar sledi

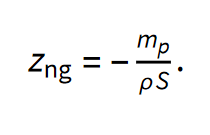
V stacionarnem režimu se torej notranja gladina vode glede na gladino v akvariju ne spreminja.

Tako je konstantna tudi hitrost curka (glej enačbo).

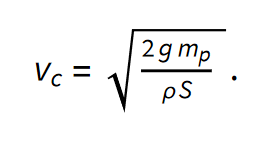
Ker je, kot smo že zapisali, v stacionarnem režimu notranja gladina pri miru, velja

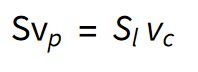
in s tem

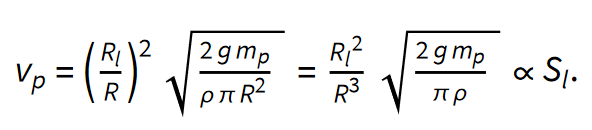
Tu je R polmer valjaste posodice, R_l pa polmer luknje.

Vidimo, da je v stacionarnem režimu hitrost potapljanja posode sorazmerna s površino luknje. To se sklada z rezultati naših meritev (glej poglavje Vpliv velikosti lukenj na čas potapljanja), kjer smo ugotovili, da je povprečna hitrost potapljanja sorazmerna s površino lukenj.

Primerjava modela in eksperimenta

Koeficient dušenja

Tega koeficienta teoretično ne znamo določiti. Zato bomo za simulacije vzeli eksperimentalno določene vrednosti β. Tabelo z vrednostmi najdete tule.

Nihajni čas

Teoretično ne bi pričakovali konstantnih časov med sosednjima nihajema, saj je

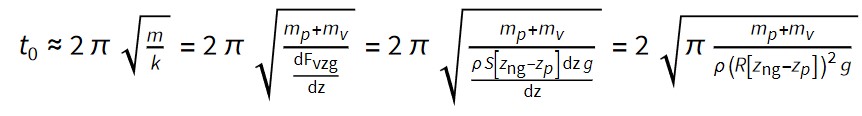
Da bi imeli konstanten nihajni čas bi se morala tako k (sorazmeren preseku S posodice na zunanji gladini), kot tudi masa m sistema hkrati spreminjati za isti faktor. Vendar pa pri eksperimentu vidimo približno enake nihajne čase.

Gibanje posodic na splošno

Za lego posodice v odvisnosti od časa dobimo naslednje grafe, kjer je modri graf teoretična napoved, oranžni pa meritev eksperimenta.

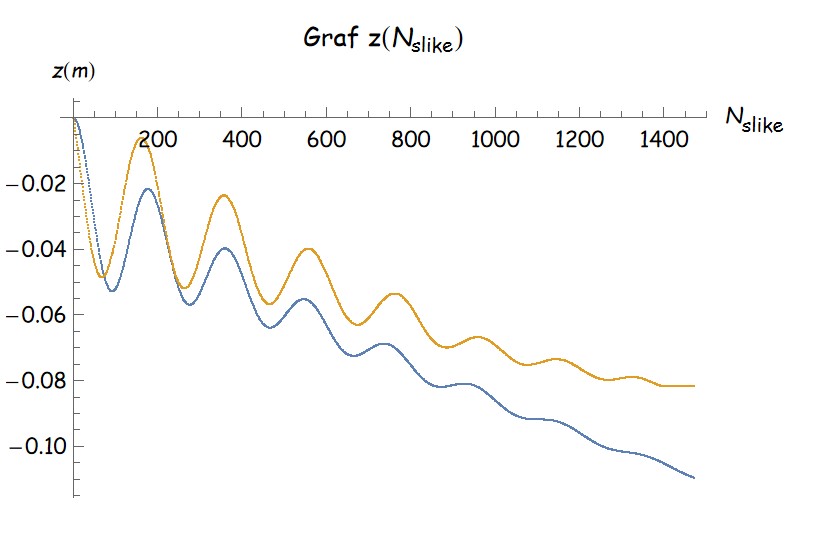
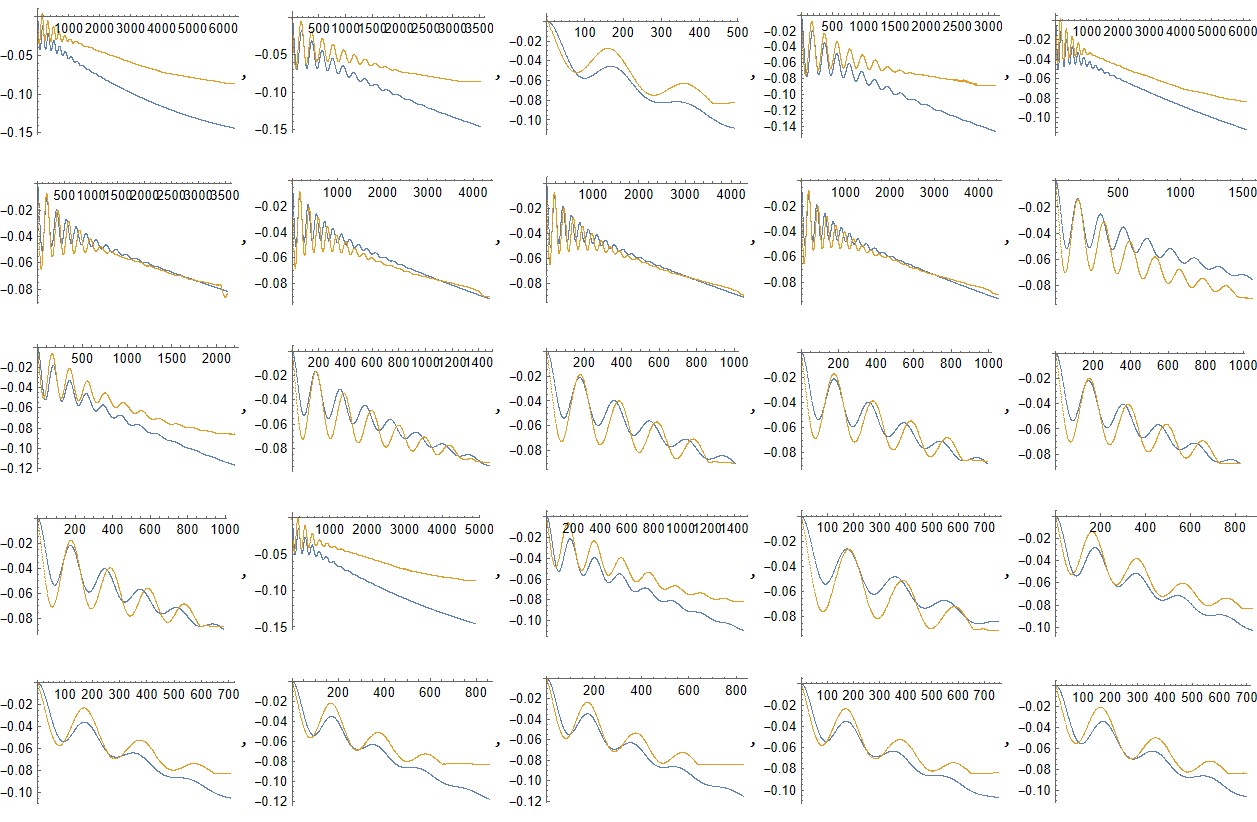
Iz grafov na sliki vidimo, da teorija precej odstopa od eksperimenta, dobimo pa kvalitativno pravilne oblike grafov. Poskusi z različnimi parametri se različno ujemajo z rezultati modela. Na prvi pogled ne opazimo jasnih vzorcev ujemanja v odvisnosti od parametrov. Iskanje vzrokov za različno ujemanje bi lahko bila nadaljna razširitev našega eksperimenta.

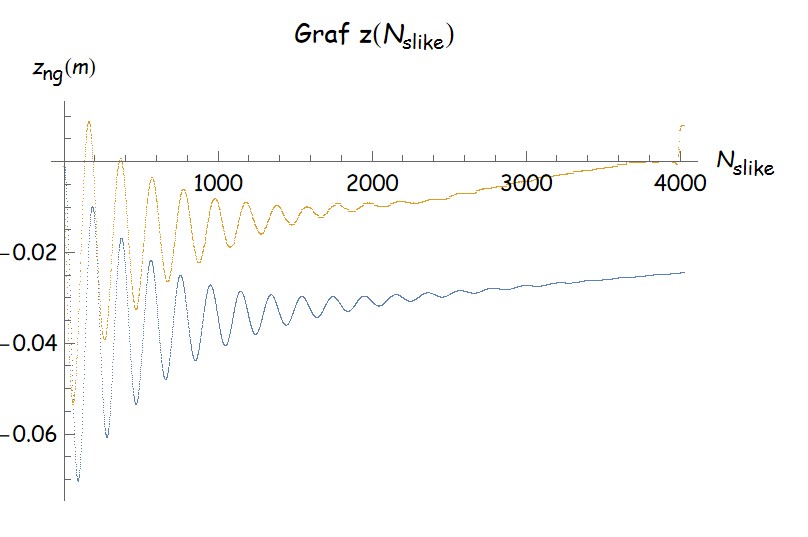
Meritve višine notranje gladine so bile precej zahtevne, zato jih nismo naredili veliko. V posodico smo dali črnilo, da je bila voda znotraj posodice vidna na posnetkih. Za natančno obdelavo teh posnetkov bi morali sprogramirati drugačen program kot smo ga uporabljali za ostale meritve. Ker nismo imeli veliko meritev in so bile te nekoliko bolj nenatančne kot ostale, se analize višine notranje gladine nismo podrobneje lotili. Pri primerjavi z modelom vidimo precejšnje ujemanje oblike grafa in odstopanje številskih vrednosti. V prihodnje bi lahko izboljšali metodo merjenja in podrobneje raziskali tudi ta pojav.