Kako temna je senca?

teorija

O osvetljenosti:

Gostota svetlobnega toka je enaka

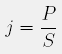
$j = \frac{P}{S}$

svetlobnemu toku na enoto ploskve, ki stoji pravokotno na smer širjenja svetlobe. V primeru točkastega svetila, ki sveti enakomerno na vse strani, velja:

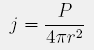
$j = \frac{P}{4 \pi r^2}$

Osvetljenost (j') ploskve S pa je definirana kot moč na enoto površine osvetljene ploskve

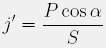
$j' =\frac{P \cos\alpha}{S}$

kjer je α kot med smerjo toka in normalo ploskve. Če kot primer ponovno vzamemo točkasto svetilo, vidimo, da osvetljenost pada z razdaljo ter s kotom, pod katerim nanjo padajo žarki

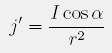
$j' =\frac{I \cos\alpha}{r^2}$

kjer je I svetilnost točkastega svetila.

Lux:

Svetila oddajajo elektromagnetna (EM) valovanja v velikem frekvenčnem razponu. Vidna svetloba je le del tega valovanja. Ker oko ni občutljivo na celoten spekter EM valovanja, je osvetljenost smiselno meriti tako kot svetlobo zaznava naše oko. Zato je bil tudi uveden lux. Lux je fiziološka enota za osvetljenost (enota je lm/m²). To pomeni da je njena vrednost prilagojena zaznavam naših čutil.

Prehod skozi polsenco:

Pri prehodu skozi polsenco lahko opazujemo več elementov. Pri našem eksperimentu smo se osredotočili na širine ter poteke prehodov (t.j. s kakšno funkcijo bi lahko opisali prehod). Zaradi tega bomo tukaj preučili ta parametra. Zavedati pa se moramo, da je treba razlikovati tudi med razpršeno svetlobo (s kakršno smo delali eksperiment) in usmerjeno svetlobo (npr. laser).

Širina prehoda:

Opazujemo le eno dimenzijo, širino. Recimo da je naša žarnica široka A in oddaljena od ovire za razdaljo A'. Če je zaslon na katerem merimo širino prehoda od ovire na drugo stran oddaljen za B', bo širina polsence enaka B, in sicer v razmerju:

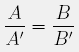
$\Frac{A}{A'} = \frac{B}{B'}$

To je razvidno iz preproste geometrije.

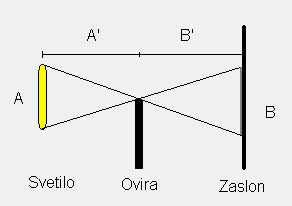
Vendar pa je svetloba valovanje in se kot taka uklanja, ko potuje mimo ovire. To bi lahko povzročilo, da bi se dejanska širina prehoda razlikovala od te, ki jo predvideva zgornja enačba. Toda odklon postane bolj očiten šele pri valovnih dolžinah, ki so reda velikosti ovire, medtem ko je valovna dolžina svetlobe reda 10^-7m. Zato so odstopanja pri svetlobi relativno majhna in jih pri ovirah, ki smo jih uporabili, ne opazimo.

Potek prehoda:

Dve enako veliki svetili naj nam bi v enakih okoliščinah dali enako širok prehod, česar pa ne moremo sklepati za potek. Le ta je odvisna od same oblike svetila. Sklepamo lahko, da je osvetljenost v neki točki sorazmerna z delom žarnice, ki osvetljuje to točko. Pri tem sklepu smo naredili kar nekaj predpostavk. Zanemarili smo dimenzije svetila v primerjavi z razdaljo, ki jo mora posamezen žarek prepotovati med svetilom in točko v kateri merimo osvetljenost. Privzeli smo, da vsi žarki naredijo enako dolgo pot. Ravno tako smo predpostavili, da svetilo sveti enakomerno po vsej svoji površini. Torej je osvetljenost sorazmerna površini svetila, ki sveti v tisto točko.

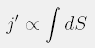
$j' \propto \int dS$

Pa poglejmo na primeru flourescentne žarnice (v nadaljevanju neonke). Če gledamo neonko iz strani, ki je obrnjena proti zaslonu, lahko rečemo, da je pravokotne oblike. Zato velja

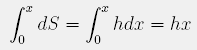
$\int_0^x dS= \int_0^x h dx = h x$

(kjer je h višina neonke, ter x parameter širine) kar pomeni, da bo osvetljenost linearno naraščala. Mlečna žarnica je približno okrogle oblike. Naj bo r polmer in x tekoči parameter po širini. Koordinatni sistem postavimo v sredino žarnice. Torej je:

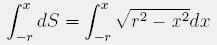
$\int_{-r}^{x} dS = \int_{-r}^{x} \sqrt{r^2 - x^2} dx$

Po integriranju dobimo:

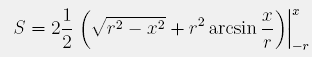
$S = 2 \frac{1}{2} \left. \left( \sqrt{r^2 - x^2} + r^2 \arcsin{\frac{x}{r}} \right) \right|_{-r}^x$

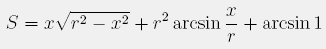
$S = x \sqrt{r^2 - x^2} + r^2 \arcsin{\frac{x}{r}} + \arcsin{1)$

Ta funkcija (ko x teče od -r do r) ima obliko

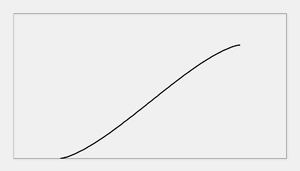
in podobno bi moral izgledati tudi prehod pri mlečni žarnici.

Pri zgornjih primerih smo predpostavili, da je oddaljenost žarnic od zaslona velika. Vprašanje je, kaj se zgodi, če dimenzije žarnice niso zanemarljive. V tem primeru vsi žarki ne prepotujejo več enako dolge poti. Poglejmo najkrajšo povprečno pot žarka. Le ta je na ‘simetrijski osi’ svetila. Pri okroglih svetilih sicer ne moremo govoriti o simetrijski osi, vendar je ta v tem primeru določena kot najmanjša razdalja med svetilom in zaslonom. Ko se po zaslonu premikamo stran od simetrijske osi, se povprečna pot žarka veča, in ker gostota svetlobnega toka z razdaljo pada, se manjša tudi osvetljenost. K temu učinku pripomore tudi to, da žarki dlje od simetrijske osi padejo na ploskev pod večjim kotom glede na normalo. Na grafu prehoda bi se to videlo kot manjšanje strmine krivulje od temnega proti svetlemu robu prehoda (velja le pri takšni postavitvi kot smo jo imeli pri poizkusu).
Do podobnega pojava pride tudi, če upoštevamo razsežnost svetila v smeri proti zaslonu (npr. pri mlečni žarnici), t.j., da ni vsaka točka svetila enako oddaljena od zaslona. V tem primeru bo osvetlitev močnejša tam, kjer bo svetilo bližje zaslonu. V primeru mlečne žarnice naj bi to pomenilo večjo strmino prehoda v srednjem delu.