Velikost deformacije telesa je odvisna od koeficienta sile F in ploskve S, na katero deluje sila v pravokotni smeri. Če je sila usmerjena pravokotno ven iz ploskve se kvocient F/S imenuje natezna napetost σ:

Če je sila usmerjena pravokotno v ploskev povzroča tlak in skrčenje telesa. V tem primeru se kvocient F/S imenuje tlak sile p:

Če je sila poševna glede na ploskev, povzroča tlak ali natezno napetost le njena projekcija v smeri pravokotnice na ploskev.
Merska enota tlaka ali natezne napetosti je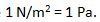

Podolgovato telo z dolžino b in prečnim presekom S raztegujemo s silo F. Kvocient raztezka x telesa in njegove prvotne dolžine b se imenuje relativni ali specifični raztezek ɛ:

Po večini je to majhno število, ki ga navadno povemo v odstotkih.
Hookov zakon pravi, da je natezna napetost premosorazmerna z relativnim raztezkom:

Sorazmernostna konstanta E je prožni modul snovi. Njegova merska enota je 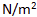in pove, kolikšna napetost je potrebna za relativni raztezek 1, to pomeni, da se telo raztegne za svojo dolžino (x=b). Hookov zakon velja samo za majhne relativne raztezke, pri večjih pa zveza med natezno napetostjo in relativnim raztezkom ni več linearna. Strmina linearnega dela krivulje σ(ɛ) podaja prožnostni modul E snovi. Pri velikih raztezkih za nadaljnje raztegovanje niso potrebne tolikšne napetosti, kot bi pričakovali po Hookovem zakonu.
Konstanta prožne vzmeti k je pri ravni žici odvisna od prožnostnega modula E, dolžine b in preseka S. Velja:

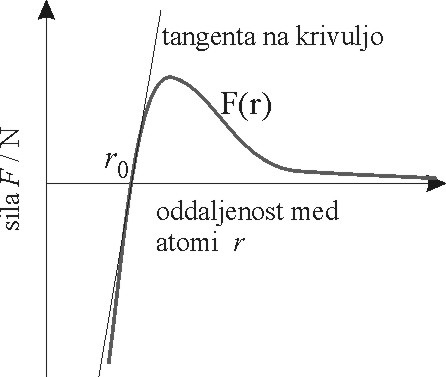
Sila med atomi F v odvisnosti od njihove medsebojne oddaljenosti r. Naklon tangente na krivuljo pri ravnotežni razdalji med atomi r0 je modul elastičnosti E. Kjer se tangenta sklada s krivuljo, velja Hookov zakon.

Hookov zakon lahko zapišemo tudi drugače, in sicer kot:

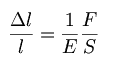
l…dolžina neobremenjenega telesa
Δl…raztezek (podaljšek, razteg) ali skrček v smeri delovanja zunanje sile F,
S…prečni presek telesa,
E…prožnostni modul.

Razmerje med relativnim raztezkom in relativnim prečnim skrčkom (zožitkom) se označuje z m

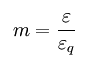
njegova obratna vrednost pa je Poissonovo število μ
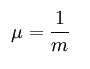