Fizika domin

Teorija

S padajočimi dominami se večina od nas sreča že v zgodnjem otroštvu. Začetno ''slepo'' navdušenje kaj hitro zamenja želja po razumevanju pojava. Na prvi pogled je mehanizem padanja domin sila enostaven, vendar se s podrobnejšo analizo porajajo vedno nova vprašanja. Zadeva je zapletena celo do te mere, da še danes ''zaposluje'' fizike v samem vrhu stroke (npr.: [1], [2], [3], [4]...). Seveda nivo znanstvenih člankov presega okvire naše naloge, zato se bomo tematike zgolj dotaknili in predstavili nekaj osnovnih principov.

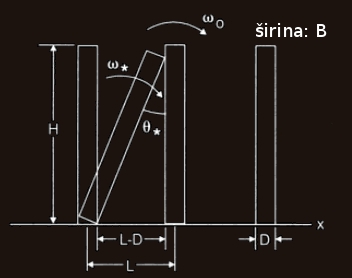
Slika 1: Shema padanja domin v vrsti na ravni podlagi. Vir [5].

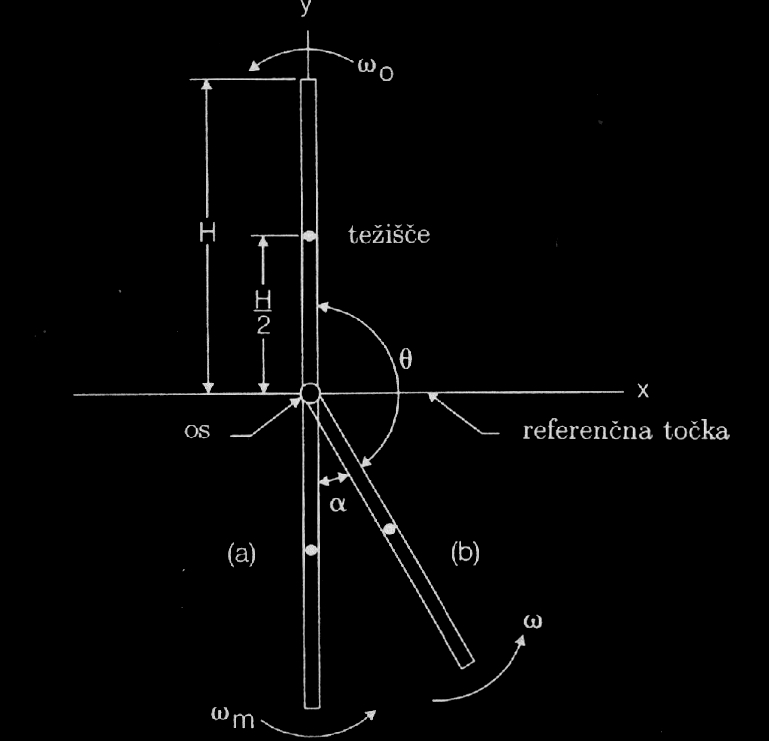
Slika 2: Padanje ene domine.

Valovna hitrost vrste padajočih domin

Denimo, da imamo dolgo vrsto domin na ravni podlagi. Razmak med centroma katerihkoli dveh zaporednih domin v vrsti je enak in ga označimo z L(glej sliko 1 za oznake). Višina posamezne domine naj bo H, njena širina B in debelina D. Privzamimo, da velja D<<H in da domine na podlagi ne zdrsavajo, temveč se pri padanju le vrtijo okrog roba med ploskvijo, ki leži na podlagi in ploskvijo, ki je obrnjena proti naslednji (še stoječi) domini. Vztrajnostni moment domine okrog te osi je \begin{equation}J=\frac{1}{3}mH^2.\end{equation} Banks (2002) predpostavlja, da na padajočo domino vpliva le ena domina pred njo, zato se bomo te poenostavitve držali tudi mi, saj se lahko sicer situacija precej zaplete [1]. Kotno hitrost padajoče domine v trenutku, ko zadane naslednjo, označimo z $\omega_\ast$ , kot med dominama pa s $\theta_\ast$. S slike 1 razberemo, da velja $$\sin \theta_\ast=\frac{(z-B)}{H}$$. Ob predpostavki, da ima domina enako energijo, ko stoji $\theta = 0$ in v trenutku trka $\theta=\theta_\ast$, lahko zapišemo izraz: \begin{equation} W_{pot1}+W_{kin1}=W_{pot2}+W_{kin2} \end{equation} ter ob upoštevanju oznak na sliki 2: \begin{equation} W_{pot1}(-\frac{H}{2})+\frac{1}{2}J\omega_m^2=W_{pot}(-\frac{H}{2}cos\alpha)+J\omega^2. \end{equation} Vemo, da velja $W_{pot}=mg$ in $J=\frac{1}{3}mH^2$. Tako dobimo: \begin{equation} \omega=\sqrt{\omega_m^2-\frac{3g}{H}(1-\cos\alpha)} \end{equation} Z zasnovo eksperimenta in definicijami količin, prikazanimi na sliki 1, se zgornja enačba zapiše kot: \begin{equation} \omega_\ast=\sqrt{\omega_m^2-\frac{3g}{H}(1+\cos\theta_\ast)} \end{equation} Kot α preberemo iz slike 2. V enačbi zgoraj se srečamo s količino $\omega_m$, kar bi bila maksimalna kotna hitrost domine v primeru, če bi bila vpeta v podnožju in prosto vrtljiva okoli te osi. V kolikor bi premikanje poganjala zgolj gravitacija, bi imela domina kotno hitrost $\omega_m$ v točki, ko bi visela navpično navzdol (pod ravnino vrste domin). Ta izraz potrebujemo zaradi povezav z energijo. Za minimalno kotno hitrost zapišemo: \begin{equation} \omega_0=\sqrt{\omega_m^2-\frac{6g}{H}}. \end{equation}

Vpeljimo še eno pomembno predpostavko: gibalna količina se v vodoravni smeri ohranja. Vemo, da velja $M=J\omega$, zato: \begin{equation} \omega_\ast \cos \theta_\ast = \omega_0. \end{equation} Z upoštevanjem gornjih relacij pridemo do enačbe: \begin{equation} \omega_m=\frac{1}{\sin\theta_\ast}\sqrt{\frac{3g}{H}[2-(1+\cos\theta_\ast)\cos^2\theta_\ast]} \end{equation} Na tem mestu preskočimo nekaj matematike, ki presega naš nivo in dobimo: \begin{equation} t_\ast=\frac{1}{2}\omega_m[K(k)-F(\phi_\ast,k)], \end{equation} kjer je $t_\ast$ čas padanja od $\theta=0$ do $\theta=\theta_\ast$ in $\phi_\ast=\alpha_\ast/2=(\pi-\theta_\ast)/2$. $K(k)$ in $F(\phi_\ast,k)$ sta popolni in nepopolni eliptični integral prve vrste. Velja tudi $k=\sqrt{6g/H}/\omega_m$. Sedaj definirajmo še iskano (valovno) hitrost: $c=(L-D)/t_\ast$ in brezdimenzijski parameter $\frac{c}{\sqrt{gH}}$. Iščemo $\frac{c}{\sqrt{gH}}=f(\frac{z}{H})$. To je analitično rešljivo in tako je nastala zvezna krivulja na grafu na grafu 1, kjer so s krogci in prekinjeno črto predstavljeni tudi merski podatki McLachlana in sod. [6]. Opazimo, da se krivulji dobro ujemata med $\frac{L}{H}=0.4$ in vsaj $\frac{L}{H}=0.85$.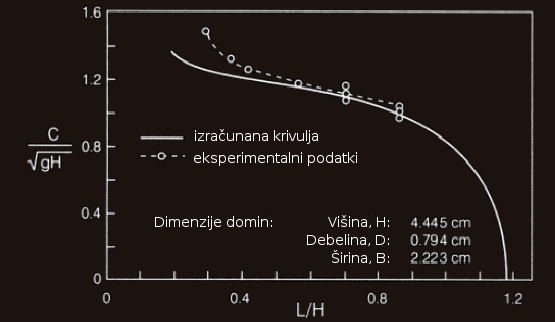

Slika 3: Primerjava rezultatov matematičnega modela valovne hitrosti padajočih domin z eksperimentalnimi podatki. Vir [5].

Tu je potrebno poudariti še nekaj. Sicer drži da se iz gornjih enačb lahko dobi $t_{\ast}$, in posledično $c$. Ampak to ni dovolj, saj lahko iz $t_{\ast}$ sklepamo o $c$ le takrat, ko je $\omega_m$ za vsako domino enak, kar pa ni vedno res, saj začetne domine ne padajo enako hitro kot kasnejše. Tej napaki smo se poskušali izogniti tako, da smo hitrost padanja domin merili šele od neke domine naprej, torej da je pred začetno merjeno domino padlo že vsaj 10 domin.

Fizika padanja ene domine

Natančno izdelano domino, katere ploskve so ravne in pravokotne ena na drugo lahko na ravni podlagi postavimo na katerokoli ploskev. Med opravljanjem praktičnega dela projektnega dela smo se med drugim ukvarjali tudi s padanjem ene domine. Domina, postavljena na najmanjšo ploskev je v stabilni legi. Pri izračunih bomo predpostavili, da je sila lepenja med domino in podlago dovolj velika, da ne pride do spodrsavanja. Domina je v stabilni legi, dokler je kot nagiba manjši od mejnega kota. Mejni kot lahko izračunamo po naslednji enačbi:

\begin{equation} arctg(θ)=\frac{D}{H}, \end{equation}

pri čemer je D debelina, H pa višina domine. Če domino nagnemo za kot, ki je manjši od mejnega kota in jo nato spustimo, se bo vrnila v začetno lego. Ko je kot nagiba enak mejnemu kotu, se domina nahaja v labilni legi, kar pomeni, da se njena lega ne bo spreminjala, če ne pride do spremembe nagiba. Takoj, ko se kot nagiba le malo spremeni, domina ne bo več v labilni legi in se vanjo ne bo več vrnila. Ustavila se bo v najbližji stabilni ali indiferentni legi. Predpostavimo, da domino nagibamo v smeri urinega kazalca. Na domino, ki je v labilni legi ne deluje navor teže, saj je prijemališče navora nad podporno točko domine. Dokler je kot nagiba manjši od mejnega kota, na domino deluje navor teže:

\begin{equation} M=\frac{mg}{2}(Hsin θ- Dcos θ). \end{equation}

Iz pogoja, da je $M=0$ iz gornje enačbe takoj sledi enačba za mejni kot. Ko kot nagiba preseže mejni kot, pa navor teže domino premika v stanje, kjer je njena potencialna energija najmanjša ($W_p=\frac{1}{2}mgD$).

S podatki o dominah, s katerimi smo delali mi, lahko naredimo teoretično napoved, v kakšni legi bo naša domina pri nekem kotu, ter kakšen je mejni kot.

H=49.18+/-0.02 mm
D=8.85+/-0.02 mm

Mejni kot:

\begin{equation} arctg(θ_0)=\frac{D}{H}=10.2±0.1° \end{equation}

Sedaj vemo, da bo domina v stabilni legi, ko se bo od navpičnice nagnila za kot θ≤10.2°, v labilni legi, ko bo kot θ=10.2±0.1° ter da bo padla po tleh, ko bo kot glede na navpičnico θ≥10.2°.

Literatura

[1] J. M. J. van Leeuwen. The domino effect. arXiv:physics/0401018v1 (2004).
[2] R. Larham. Validation of a model of the domino efect? arXiv:0803.2898v1 (2008).
[3] Charles W. Bert. Falling dominoes. SIAM Review, 28, 219 (1986).
[4] D. E. Shaw. Mechanics of a chain of dominoes. American Journal of Physics, 46, 640 (1978).
[5] R.B. Banks. Towing Icebergs, Falling Dominoes, and Other Adventures in Applied Mathematics. Princeton paperbacks. Princeton University Press, 2002.
[6] B. G. McLachlan, G. Beaupre, A. B. Cox, and L. Gore. Falling dominoes. SIAM Review, 25, 403 (1983).