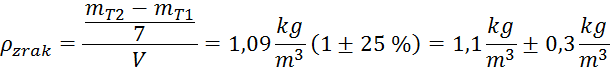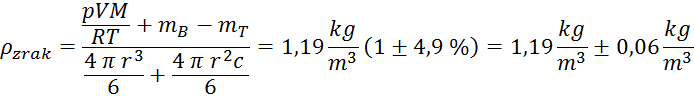Rezultati
Prvi poskus Drugi poskus
Tretji poskus
Četrti poskus
Na vrh ↑
Tukaj
bomo predstavili meritve in računske rezultate vseh štirih eksperimentov. Opise
poskusov si lahko preberete tukaj, teoretične
osnove pa tukaj. Povzetek rezultatov je v zaključku.
Ocenjevanje merskih napak:
Napake
rezultatov so pri vseh spodaj opisanih izračunih ocenjene po pravilu
najšibkejšega člena. Pravilo pravi, da je relativna napaka rezultata enaka
največji relativni napaki meritev.
Če
imamo meritve 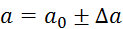 ,
, 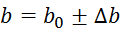 in
in 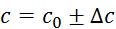 in želimo izračunati
npr. vrednost izraza
in želimo izračunati
npr. vrednost izraza 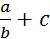 (lahko bi nastopal
kakršenkoli drug izraz), najprej izračunamo relativne napake meritev
(lahko bi nastopal
kakršenkoli drug izraz), najprej izračunamo relativne napake meritev 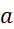 ,
,
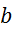 in
in 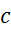 ,
ki znašajo
,
ki znašajo 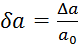 ,
, 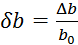 in
in 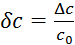 . Nato preverimo,
katera relativna napaka je največja (tista meritev je torej najšibkejši člen)
in največja relativna napaka meritev postane tudi relativna napaka končnega
izračuna. Če je med relativnimi napakami največja npr.
. Nato preverimo,
katera relativna napaka je največja (tista meritev je torej najšibkejši člen)
in največja relativna napaka meritev postane tudi relativna napaka končnega
izračuna. Če je med relativnimi napakami največja npr. 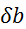 ,
velja, da je
,
velja, da je 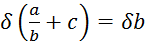 . Izraz
. Izraz 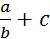 z mersko napako torej
zapišemo takole:
z mersko napako torej
zapišemo takole: 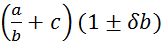 .
.
V
nadaljevanju bodo med zbranimi relativnimi napakami pod izračunom največje
relativne napake obarvane rdeče.
Prvi poskus – spreminjanje vzgona v odvisnosti od
spreminjanja prostornine balona
Prvi poskus
Drugi poskus
Tretji poskus
Četrti
poskus
Na vrh ↑
Opis
eksperimenta lahko najdete tukaj.
Meritev in izračun začetnega volumna balona:
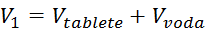
Volumen tablet, ki imajo obliko valja s premerom 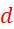 in višino
in višino 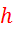 , določimo
po enačbi (v balon smo dali 5 tablet):
, določimo
po enačbi (v balon smo dali 5 tablet):
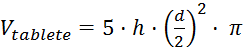
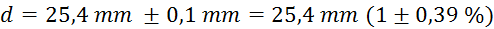 (kljunasto merilo
je natančno na desetinko milimetra) ki znaša
5,9 %ka je enaka največji relativni napaki meritev, torej napaki meritve
(kljunasto merilo
je natančno na desetinko milimetra) ki znaša
5,9 %ka je enaka največji relativni napaki meritev, torej napaki meritve
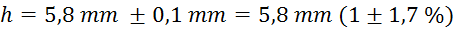 (kljunasto merilo
je natančno na desetinko milimetra)
(kljunasto merilo
je natančno na desetinko milimetra)
Volumen vode pa najlažje natančno določimo iz mase v balon dodane
vode, če predpostavimo, da je gostota vode 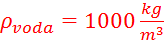 :
:
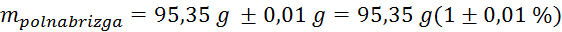 (tehtnica je
natančna na stotinko grama)
(tehtnica je
natančna na stotinko grama)
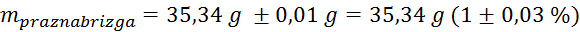 (tehtnica je
natančna na stotinko grama)
(tehtnica je
natančna na stotinko grama)
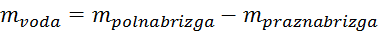
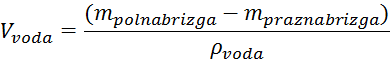
Začetni volumen balona torej znaša:
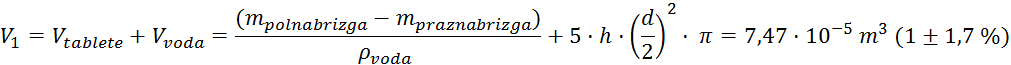
Relativne
napake vseh meritev, potrebnih za izračun začetnega volumna, znašajo:
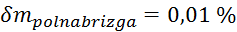 ,
, 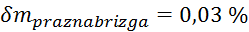 ,
, 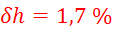 ,
, 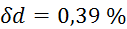
Relativna
napaka začetnega volumna je enaka največji relativni napaki meritev, tj. napaki
debeline tablete 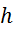 , ki znaša
, ki znaša 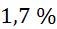 .
.
Sprememba mase pri tehtanju balona:
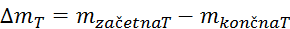
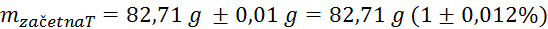 (tehtnica je natančna na stotinko
grama)
(tehtnica je natančna na stotinko
grama)
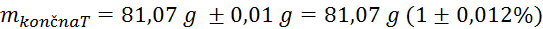 (tehtnica je natančna na stotinko
grama)
(tehtnica je natančna na stotinko
grama)
Končni volumen balona določimo kot volumen elipsoida (predpostavimo,
da balon zavzema obliko elipsoida z dvema polosema 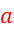 in eno
in eno 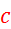 )
)
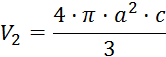
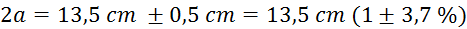 (natančnost obrisa
sence na tabli je pol centimetra)
(natančnost obrisa
sence na tabli je pol centimetra)
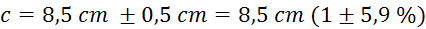 (natančnost
obrisa sence na tabli je pol centimetra)
(natančnost
obrisa sence na tabli je pol centimetra)
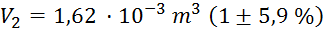
Relativne
napake vseh meritev, potrebnih za izračun končnega volumna, znašajo:
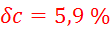 ,
, 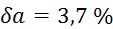
Relativna
napaka končnega volumna je enaka največji relativni napaki meritev, torej
napaki meritve 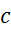 , ki znaša
, ki znaša 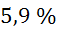 .
.
Izračun gostote zraka:
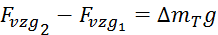
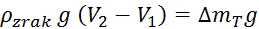
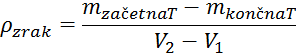
Gostota zraka:
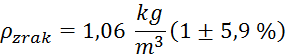
Relativne
napake vseh meritev, potrebnih za izračun gostote, znašajo:
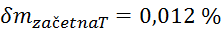 ,
, 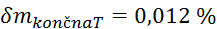 ,
, 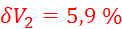 ,
, 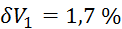
Relativna
napaka gostote je enaka največji relativni napaki med meritvami, tj. relativni
napaki končnega volumna 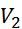 , ki znaša
, ki znaša 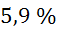 ,
,
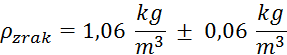
Drugi poskus – tehtanje zraka
Prvi
poskus
Drugi poskus
Tretji poskus
Četrti
poskus
Na vrh ↑
Opis eksperimenta,
izpeljave nekaterih enačb in opis oznak lahko najdete tukaj.
Meritve za
izračun volumna enega vpiha:
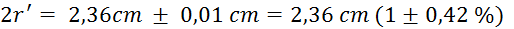 (
(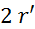 - premer bata
tlačilke + debelina stene tlačilke) (kljunasto
merilo je natančno na desetinko milimetra)
- premer bata
tlačilke + debelina stene tlačilke) (kljunasto
merilo je natančno na desetinko milimetra)
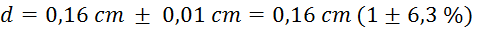 (
(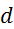 -
debelina stene tlačilke) (kljunasto merilo je natančno na
desetinko milimetra)
-
debelina stene tlačilke) (kljunasto merilo je natančno na
desetinko milimetra)
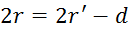
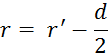
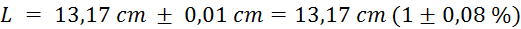 (kljunasto
merilo je natančno na desetinko milimetra)
(kljunasto
merilo je natančno na desetinko milimetra)
Izračun
volumna tlačilke:
Volumen
tlačilke:
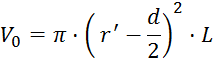
, znaša
tve
Volumen
enega vpiha tlačilke s popravkom povratnega odmika 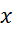 :
:
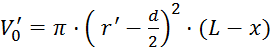
Volumen
skupno napihanega zraka po 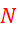 vpihih za
odmik
vpihih za
odmik 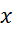 pri
pri 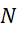 -tem
vpihu (
-tem
vpihu (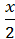 je povprečen odmik):
je povprečen odmik):
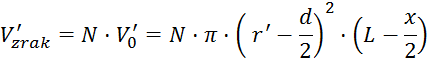
Gostota
zraka:
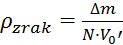 (
(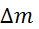 – razlika mas;
– razlika mas; 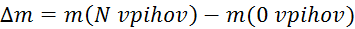 )
)
Prvi niz
meritev mase v odvisnosti od volumna vpihanega zraka in izračun gostote:
|
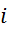
|
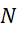
|
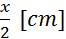 (merjenje je
zaradi zahtevnega reliefa zahtevno in zato natančno le na 5 mm) (merjenje je
zaradi zahtevnega reliefa zahtevno in zato natančno le na 5 mm)
|
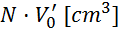
|
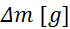 (tehtnica je
natančna na stotinko grama) (tehtnica je
natančna na stotinko grama)
|
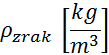
|
|
1
|
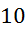
|
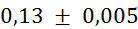
|
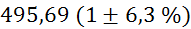
|
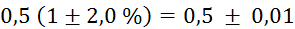
|
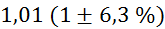
|
|
2
|
|
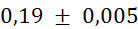
|
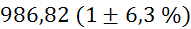
|
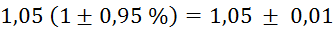
|
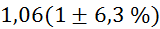
|
|
3
|
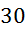
|
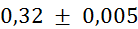
|
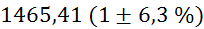
|
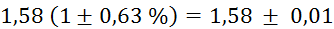
|
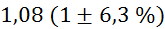
|
|
4
|
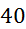
|
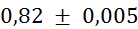
|
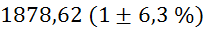
|
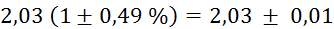
|
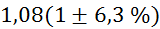
|
|
5
|
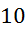
|
|
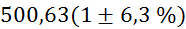
|
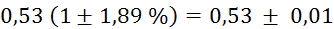
|
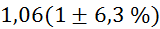
|
|
6
|
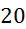
|
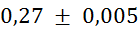
|
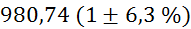
|
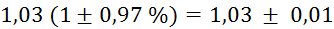
|
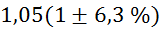
|
|
7
|
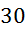
|
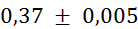
|
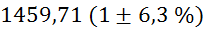
|
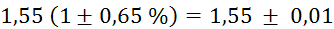
|
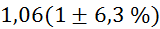
|
|
8
|
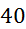
|
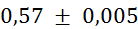
|
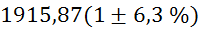
|
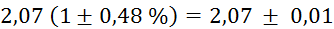
|
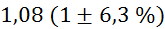
|
Relativne
napake vseh meritev, potrebnih za izračun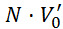 , znašajo:
, znašajo:
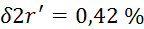 ,
, 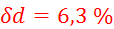 ,
, 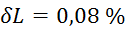 , vsi
, vsi 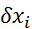 za
za 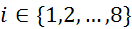 so manjši ali enaki
od
so manjši ali enaki
od 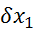 ,ki znaša
,ki znaša 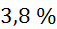 .
.
Relativne napake pri
volumnih 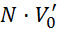 so določene kot
največje relativne napake meritev, iz katerih volumen izračunamo. Med njimi ima
torej največjo relativno napako za vsak
so določene kot
največje relativne napake meritev, iz katerih volumen izračunamo. Med njimi ima
torej največjo relativno napako za vsak 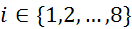 meritev
debeline tlačilke
meritev
debeline tlačilke 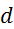 , ki znaša
, ki znaša 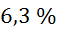 . Tako je napaka
volumna
. Tako je napaka
volumna 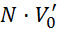 enaka
enaka 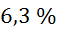
Relativne napake vseh
izračunov, potrebnih za izračun gostote zraka, znašajo:
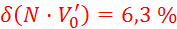 za
vsak
za
vsak 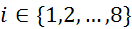 , relativne napake
, relativne napake 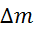 pa znašajo med
pa znašajo med 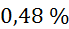 in
in 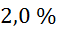 (glej zgornjo
preglednico)
(glej zgornjo
preglednico)
Relativne napake
gostot so enake največji relativni napaki med meritvami, potrebnimi za izračun gostote.
Napako gostote torej določa napaka volumna 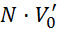 , ki znaša
, ki znaša 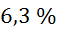 .
.
Gostota:
Relativna napaka
povprečne gostote je enaka napakam vseh posameznih gostot iz meritev.
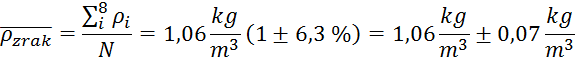
Drugi
niz meritev mase v odvisnosti od volumna vpihanega zraka in izračun
gostote(trikratna ponovitev meritve brez spreminjanja števila vpihov) :
Relativne napake pri
volumnih 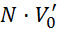 so določene kot
največje relativne napake meritev, iz katerih volumen izračunamo. Med njimi ima
največjo relativno napako pri vseh primerih meritev debeline tlačilke
so določene kot
največje relativne napake meritev, iz katerih volumen izračunamo. Med njimi ima
največjo relativno napako pri vseh primerih meritev debeline tlačilke 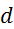 ,
ki znaša
,
ki znaša 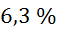 .
.
Relativne napake gostot so enake največji relativni napaki med meritvami,
potrebnimi za izračun gostote. Napako gostote posledično določa napaka volumna 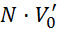 , ki znaša
, ki znaša 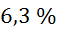 .
.
Relativne
napake vseh meritev, potrebnih za izračun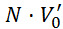 , znašajo:
, znašajo:
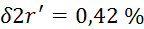 ,
, 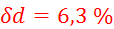 ,
, 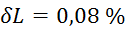 , vsi
, vsi 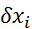 za
za 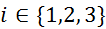 so manjši ali enaki
od
so manjši ali enaki
od 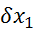 ,ki znaša
,ki znaša 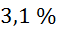 .
.
Relativne napake pri
volumnih 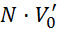 so določene kot
največje relativne napake meritev, iz katerih volumen izračunamo. Med njimi ima
torej največjo relativno napako za vsak
so določene kot
največje relativne napake meritev, iz katerih volumen izračunamo. Med njimi ima
torej največjo relativno napako za vsak 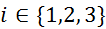 meritev
debeline tlačilke
meritev
debeline tlačilke 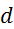 , ki znaša
, ki znaša 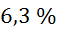 . Tako je napaka
volumna
. Tako je napaka
volumna 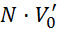 enaka
enaka 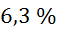
Relativne napake vseh
izračunov, potrebnih za izračun gostote zraka, znašajo:
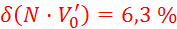 za
vsak
za
vsak 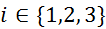 , relativne napake
, relativne napake 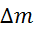 pa znašajo med
pa znašajo med 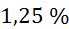 in
in 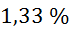 (glej zgornjo
preglednico)
(glej zgornjo
preglednico)
Relativne napake
gostot so enake največji relativni napaki med meritvami, potrebnimi za izračun
gostote. Napako gostote torej določa napaka volumna 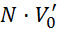 , ki znaša
, ki znaša 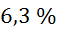 .
.
Gostota:
Relativna napaka
povprečne gostote je enaka napakam vseh posameznih gostot iz meritev.
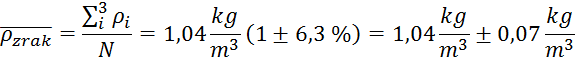
Tretji poskus – tehtanje zračnice pri različnih tlakih
Prvi poskus
Drugi poskus
Tretji poskus
Četrti
poskus
Na vrh ↑
Opis eksperimenta
lahko najdete tukaj.
Meritve
mase v odvisnosti od tlaka:
|
tlak
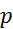 (merilec tlaka ima na skali
označene le četrtinke bara, zato je natančnost majhna) (merilec tlaka ima na skali
označene le četrtinke bara, zato je natančnost majhna)
|
masa
kolesa 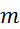 (tehtnica je
natančna na en gram) (tehtnica je
natančna na en gram)
|
|
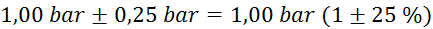
|
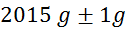
|
|
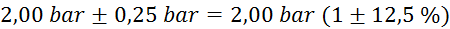
|
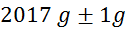
|
|
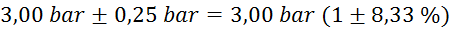
|
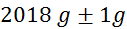
|
|
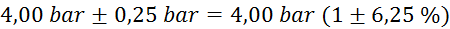
|
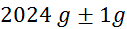
|
|
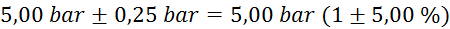
|
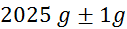
|
|
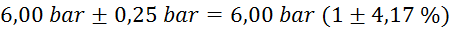
|
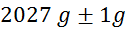
|
|
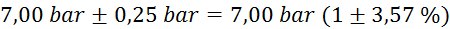
|
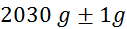
|
|
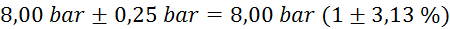
|
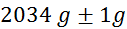
|
Po izpeljavi, ki je
predstavljena pri opisu
poskusa, lahko maso zraka v zračnici
pri normalnih pogojih izračunamo takole:
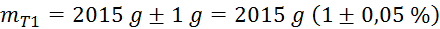 (tehtnica
je natančna na en gram)
(tehtnica
je natančna na en gram)
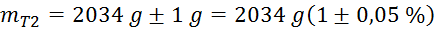 (tehtnica je
natančna na en gram)
(tehtnica je
natančna na en gram)
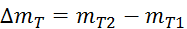
�_eline plašča, ki znaša ajvečji relativni napaki
meritev, tj. tivni napaki meritevza izračun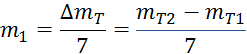
(Zadnja
enačba ni popolnoma natančna. Ob pogledu na izpeljavo ugotovimo, da je sedmica
v imenovalcu v resnici odvisna od tlaka, zato je relativna napaka izračuna 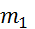 enaka največji napaki
meritev tlaka, tj. meritvi tlaka pri
enaka največji napaki
meritev tlaka, tj. meritvi tlaka pri 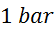 , ki znaša
, ki znaša 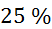 .)
.)
Volumen
zračnice smo določili po formuli za volumen torusa (predpostavili smo, da ima
zračnica obliko torusa):
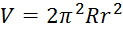
Določitev 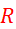 iz obsegov:
iz obsegov:
Največji možni R
(po plašču):
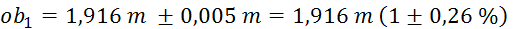 (meritev s šiviljskim
metrom je natančna na pol centimetra)
(meritev s šiviljskim
metrom je natančna na pol centimetra) 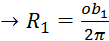
Najmanjši možni R
(po obroču, »feltni«):
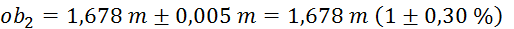 (meritev s šiviljskim
metrom je natančna na pol centimetra)
(meritev s šiviljskim
metrom je natančna na pol centimetra)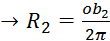
Povprečen R:
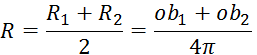
Ocena 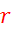 :
:
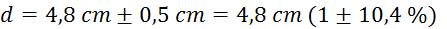 (širina gume skupaj s
plaščem) (napaka nastane zaradi zahtevnosti merjenja na neravnem reliefu
gume, merjeno kar s šiviljskim metrom)
(širina gume skupaj s
plaščem) (napaka nastane zaradi zahtevnosti merjenja na neravnem reliefu
gume, merjeno kar s šiviljskim metrom)
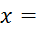 debelina
plašča
debelina
plašča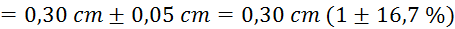 (debelina plašča
je izmerjena s kljunastim merilom, zaradi neravnega reliefa pa ni povsod enaka
in niha za
(debelina plašča
je izmerjena s kljunastim merilom, zaradi neravnega reliefa pa ni povsod enaka
in niha za 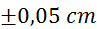 )
)
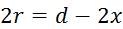
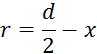
Izračun
volumna:
Relativna napaka
izračuna je po pravilu najšibkejšega člena enaka največji relativni napaki meritev,
tj. napaki debeline plašča, ki znaša 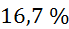 .
.
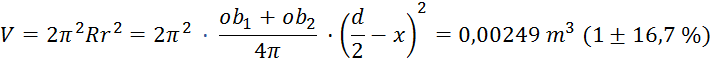
Gostota
zraka:
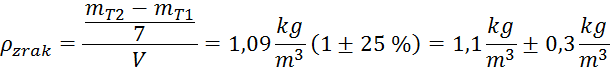
Relativne napake
meritev, potrebnih za izračun gostote, znašajo:
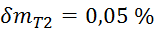 ,
,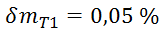 ,
,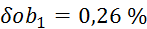 ,
, 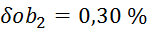 ,
, 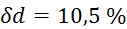 ,
, 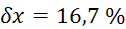 , relativne napake
tlakov pa so manjše manjše oz. enake
, relativne napake
tlakov pa so manjše manjše oz. enake  (glej zgornjo
tabelo).
(glej zgornjo
tabelo).
Relativna napaka
gostote je enaka največji relativni napaki meritev, tj. napaki izraza 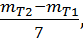 ki je sicer odvisen meritve
tlaka, napaka tlaka pri
ki je sicer odvisen meritve
tlaka, napaka tlaka pri 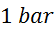 pa znaša
pa znaša 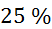 .
.
Četrti poskus – tehtanje
napihnjenega balona in razlika gostote zraka v balonu in izven njega
Prvi poskus
Drugi poskus
Tretji poskus
Četrti
poskus
Na vrh ↑
Opis eksperimenta
lahko najdete tukaj.
Izmerjeni
podatki:
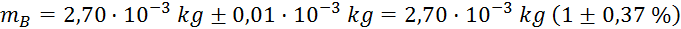 (tehtnica je
natančna na stotinko grama)
(tehtnica je
natančna na stotinko grama)
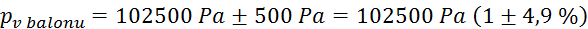 (merilec tlaka je
bolj natančen, vendar meritev tlaka niha)
(merilec tlaka je
bolj natančen, vendar meritev tlaka niha)
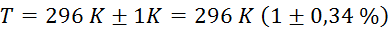 (termometer je
natančen na 1°C)
(termometer je
natančen na 1°C)
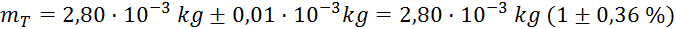 (tehtnica je natančna na stotinko
grama)
(tehtnica je natančna na stotinko
grama)
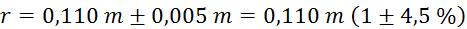 (natančnost obrisa sence na tabli je
pol centimetra)
(natančnost obrisa sence na tabli je
pol centimetra)
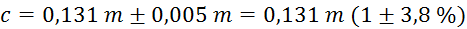 (natančnost obrisa sence na tabli je
pol centimetra)
(natančnost obrisa sence na tabli je
pol centimetra)
Izračun
volumna balona (izpeljava pri opisu poskusa):
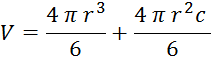
Izračun
gostote po enačbi (izpeljava pri opisu eksperimenta, privzamemo
pa, da je 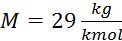 in splošna plinska
konstanta
in splošna plinska
konstanta 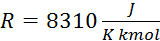 ):
):
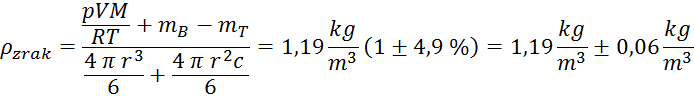
Relativne napake
meritev, potrebnih za izračun gostote, znašajo:
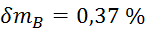 ,
, 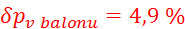 ,
, 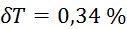 ,
, 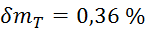 ,
, 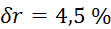 ,
, 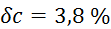 .
.
Relativna
napaka gostote je enaka največji relativni napaki meritev, tj. napaki meritve
tlaka v balonu, ki znaša 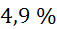 .
.
Prvi poskus
Drugi poskus
Tretji poskus
Četrti
poskus
Na vrh ↑
![]() ,
, ![]() in
in ![]() in želimo izračunati
npr. vrednost izraza
in želimo izračunati
npr. vrednost izraza ![]() (lahko bi nastopal
kakršenkoli drug izraz), najprej izračunamo relativne napake meritev
(lahko bi nastopal
kakršenkoli drug izraz), najprej izračunamo relativne napake meritev ![]() ,
,
![]() in
in ![]() ,
ki znašajo
,
ki znašajo ![]() ,
, ![]() in
in ![]() . Nato preverimo,
katera relativna napaka je največja (tista meritev je torej najšibkejši člen)
in največja relativna napaka meritev postane tudi relativna napaka končnega
izračuna. Če je med relativnimi napakami največja npr.
. Nato preverimo,
katera relativna napaka je največja (tista meritev je torej najšibkejši člen)
in največja relativna napaka meritev postane tudi relativna napaka končnega
izračuna. Če je med relativnimi napakami največja npr. ![]() ,
velja, da je
,
velja, da je ![]() . Izraz
. Izraz ![]() z mersko napako torej
zapišemo takole:
z mersko napako torej
zapišemo takole: ![]() .
.![]()
![]() in višino
in višino ![]() , določimo
po enačbi (v balon smo dali 5 tablet):
, določimo
po enačbi (v balon smo dali 5 tablet):![]()
![]() (kljunasto merilo
je natančno na desetinko milimetra)
(kljunasto merilo
je natančno na desetinko milimetra)![]() (kljunasto merilo
je natančno na desetinko milimetra)
(kljunasto merilo
je natančno na desetinko milimetra)![]() :
:![]() (tehtnica je
natančna na stotinko grama)
(tehtnica je
natančna na stotinko grama)![]() (tehtnica je
natančna na stotinko grama)
(tehtnica je
natančna na stotinko grama)![]()
![]()
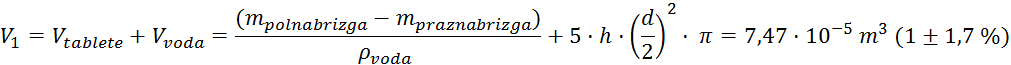
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() , ki znaša
, ki znaša ![]() .
. ![]()
![]() (tehtnica je natančna na stotinko
grama)
(tehtnica je natančna na stotinko
grama)![]() (tehtnica je natančna na stotinko
grama)
(tehtnica je natančna na stotinko
grama)![]() in eno
in eno ![]() )
)![]()
![]() (natančnost obrisa
sence na tabli je pol centimetra)
(natančnost obrisa
sence na tabli je pol centimetra)![]() (natančnost
obrisa sence na tabli je pol centimetra)
(natančnost
obrisa sence na tabli je pol centimetra)![]()
![]() ,
, ![]()
![]() , ki znaša
, ki znaša ![]() .
.![]()
![]()
![]()