Hidravlični skok

V kanalu: Teoretični pristop | Merjenje | Hipoteze | Rezultati | Ugotovitve

Potek meritev

je bil sledeč:

Pri posameznem pretoku tekočine iz vira, katerega smo arbitrarno izbrali z odprtjem ventila, smo večkrat izmerili pretočno hitrost. Dejanske hitrosti torej nismo poznali, kar že nakazuje, da bi eksperiment korenito izboljšali z elektronsko regulacijo pretoka. V nadaljevanju je podan primer meritev pri enem od izbranih pretokov.

Primer meritev pri določeni hitrosti dotoka:

t[s]	V[L]	Q[]
3,37	0,102	0,030267
3,5	0,1	0,028571
3,98	0,117	0,029397
3,6	0,105	0,029167
3,68	0,103	0,027989
3,9	0,11	0,028205
3,92	0,112	0,028571

Takšne meritve smo izvedli pri 6 različnih hitrostih pretoka. Na osnovi povprečnih pretokov pri posameznem odprtju ventila, smo nadalje izračunali pristoječe ploščinske pretoke q - pretoke na enoto širine, ki je za primer pravokotnega kanala stalna.

Izračunali smo ustrezne ploščinske pretoke q- pretoke na enoto širine, ki je za primer pravokotnega kanala stalna.

Pri posamezni hitrosti dotoka smo nato spreminjali višino zapornice ter tako varirali višino superkritične tekočine – y₁. Določili smo kritično višino y_c, ter izračunali konjugirane višine y₂, Froudova šrevila Fr, specifične sile M za posamezne višine in pristoječe brezdimenzijske specifične energije E . Izmerjene vrednosti višin v odvisnosti od specifične sile smo primerjali s teoretično konvergenčno linijo

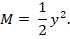
Izmerjene vrednosti višin v odvisnosti od E pa smo primerjali s teoretično konvergenčno linijo

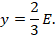
q	y1 hipotetika	Fr	y2 hipotetika	M1	M2- preizkus	yc	Mc	Ey1	Ey2
0,000283	0,0005	8,089949	0,005476	1,65	1,65	0,002015	6,09012	0,016862	0,005612
	0,0009	3,34994	0,003837	9,49	9,49			0,00595	0,004115
	0,0003	17,4068	0,007237	2,73	2,73			0,045749	0,007315
	0,001	2,860229	0,003576	8,68	8,68			0,00509	0,003896
	0,0015	1,556911	0,002637	6,58	6,58			0,003318	0,003225
0,000326	0,0005	9,307539	0,006336	2,18	2,18	0,002212	7,34194	0,022158	0,006471
	0,0009	3,854128	0,004476	1,24	1,24			0,007584	0,004746
	0,0003	20,02664	0,008348	3,61	3,61			0,06046	0,008426
	0,001	3,290712	0,004181	1,13	1,13			0,006414	0,00449
	0,0015	1,791237	0,003123	8,34	8,34			0,003906	0,003678
0,000212	0,0005	6,055376	0,004039	9,29	9,29	0,001661	4,13891	0,009667	0,00418
	0,0009	2,507451	0,002773	5,5	5,5			0,003729	0,003071
	0,0003	13,0291	0,00538	1,53	1,53			0,025764	0,005459
	0,001	2,140899	0,002569	5,08	5,08			0,003292	0,002916
	0,0015	1,165358	0,001833	4,18	4,18			0,002519	0,002515
0,00023	0,0005	6,576908	0,004407	1,09	1,09	0,001755	4,6209	0,011314	0,004546
	0,0009	2,72341	0,003045	6,41	6,41			0,004238	0,003337
	0,0003	14,15125	0,005856	1,81	1,81			0,030339	0,005935
	0,001	2,325288	0,002826	5,91	5,91			0,003703	0,003165
	0,0015	1,265727	0,002038	4,73	4,73			0,002702	0,002689
0,000246	0,0005	7,026984	0,004725	1,25	1,25	0,001834	5,04727	0,012845	0,004863
	0,0009	2,90978	0,003281	7,26	7,26			0,00471	0,003568
	0,0003	15,11966	0,006266	2,06	2,06			0,034591	0,006345
	0,001	2,484414	0,003049	6,67	6,67			0,004086	0,003381
	0,0015	1,352344	0,002215	5,24	5,24			0,002872	0,002844
0,000725	0,0005	20,71063	0,014397	0,000107	0,000107	0,003771	2,13283	0,107733	0,014526
	0,0009	8,575995	0,010475	6	6			0,033996	0,010719
	0,0003	44,56218	0,018757	0,000179	0,000179			0,298168	0,018833
	0,001	7,322313	0,009867	5,41	5,41			0,027808	0,010143
	0,0015	3,985762	0,007738	3,69	3,69			0,013415	0,008186
	0,002	2,588829	0,00639	2,88	2,88			0,008702	0,007047
	0,0025	1,852415	0,005417	2,46	2,46			0,006789	0,006331

Graf M-y:

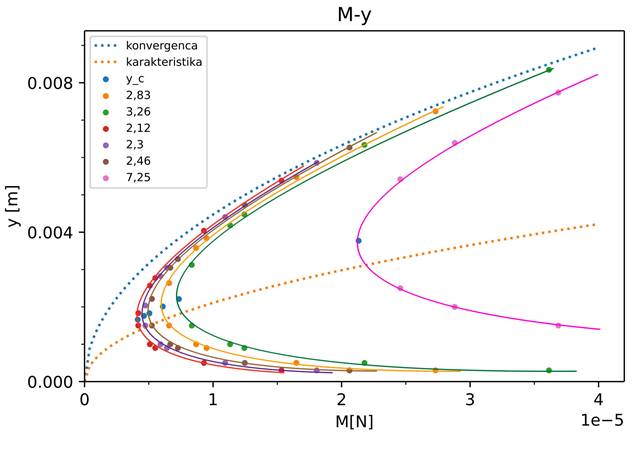
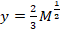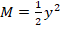karakteristika – , konvergenca - , ostale krivulje so zveze konjugiranih višin in specifičnih sil pri tabeliranih vrednostih q. Eksperimetnalne vrednosti (točke ) pri enakem M so konjugirane višine. Modre točke predstavljajo kritično višino – Fr=1.

Opomba: N označuje .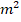

Graf E-y:

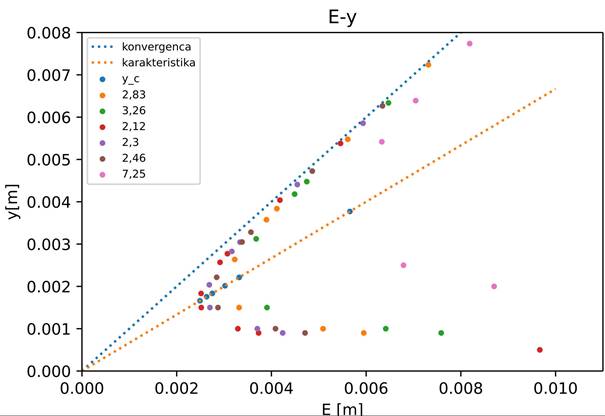
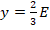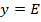karakteristika – , konvergenca - , ostale krivulje so zveze konjugiranih višin in specifičnih energij pri tabeliranih vrednostih q. Eksperimetnalne vrednosti (točke ) pri enaki vrednosti specifične energije so alternirane višine. Modre točke so kritična višina – Fr=1.