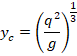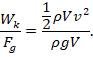|
|
Hidravlični skok |
|
| Naloga | Uvod | Osnovne ideje
| Prva opažanja | V koritu | V kanalu: Teoretični pristop | Merjenje
| Hipoteze | Rezultati | Ugotovitve | Zaključek | |
|
|
Pri
teoriji izhajamo iz Newtonovih zakonov in Bernoullijeve enačbe. Velja
ohranitev gibalne količine.
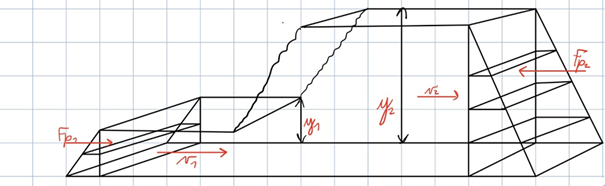
Model hidravličnega
skoka in pristoječe fizikalne količine. (V nadaljevanju izpeljave obravnavamo isto- in nasprotiležne
vektorje, zato brez škode za splošnost vektorski znak izpustimo). Pri doprinosu sil zanemarimo silo trenja in vpliv teže:
Silo potiska definiramo kot:
Upoštevamo
kontinuitetno enačbo za volumski tok:
Upoštevamo kontinuitetno enačbo za volumski tok:
Volumski tok lahko zreduciramo na dve dimenziji, saj je širina
kanala
Nekoliko preuredimo in dobimo pomemben izraz o ohranitvi
gibalne količine(momenta) v hidravliki odprtih kanalov:
Vidimo, da se moment res ohranja, višini Iz zgornje enačbe razberemo tudi obnašanje v limiti:
Hitrost in globina (višina) tekočine sta povezani v relacijo
podano kot brezdimenzijsko Froudovo število:
Pri tem velja naslednje: 1.
2.
3.
Z upoštevanjem zadnjega, kjer sta konjugirani višini enaki,
enaki pa sta tudi fazna (propagation velocity) in grupna (bulk velocity)
hitrost gravitacijskih valov, dobimo izraz za kritično višino:
Z nekaj matematičnega preoblikovanja enačbe za ohranitev
specifične sile ter upoštevanjem kontinuitetne relacije pridobimo pomembno
zvezo med konjugiranima višinama in Froudovim številom:
Z inženirskega stališča je ključna obravnava energij pri
pojavu. Pri tem definiramo kinetično energijo na enoto teže:
Definiramo še gostoto potencialne energije:
Od koder lahko na enoto teže izrazimo tudi potenicalno
energijo:
Iz energijskega zakona, kjer zanemarimo izgube na račun trenja
sledi:
Oziroma:
|
|
|
|
|