Hidravlični skok

V koritu: Teoretični pristop | Merjenje | Hipoteze | Rezultati | Ugotovitve

Predpostavimo, da imamo opravka z idealno/ neviskozno tekočino. Narišemo skico in definiramo oznake:

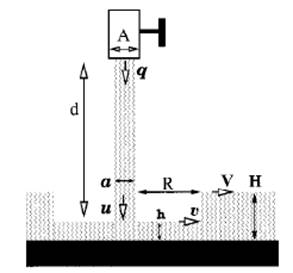
Skica prikazuje shemo poskusa za idealno tekočino, kjer predpostavimo, da se premer curka s časom ne spreminja.

Višino padanja curka definiramo kot d, razdaljo med hidravličnim skokom (robom hidravličnega kroga) in robom curka definiramo kot R. Višino gladine tik pred hidravličnim skokom definiramo kot h, višino tik po skoku pa kot H.

Hitrost curka, ko zapusti šobo, označimo z , hitrost curka tik preden zadane dno umivalnika pa označimo z u. Hitrost toka tik pred hidravličnim skokom označimo z v, hitrost toka po skoku pa z V.

Z oznako q označimo volumski pretok curka.

Za računanje vzamemo dva cilindrična razdelka v okolici območja R; prvi razdelek naj bo pred hidravličnim skokom, drugi pa po njem. Privzamemo, da velja zakon o ohranitvi gibalne količine in zapišemo enačbo:

Kjer G predstavlja gibalno količino, t je čas, ρ je gostota tekočine, in pa sta sunka zunanjih sil pred () in po () hidravličnem skoku.

Pri tem sta

Kjer g predstavlja gravitacijski pospešek.

Predpostavimo, da velja poenostavitev

Po kontinuitetni enačbi torej velja

Iz česar pa sledi

Iz trditev in pa lahko ohranitev gibalne količine zapišemo kot

Iz kontinuitetne enačbe sledi

Iz česar pa lahko izrazimo

Ko to vstavimo v relacijo , dobimo

Predpostavimo sedaj še, da imamo opravka z viskozno tekočino:

Narišemo skico in definiramo oznake:

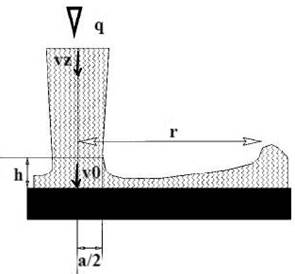
Skica prikazuje shemo poskusa za viskozno tekočino, kjer q predstavlja volumski pretok curka, r predstavlja radij hidravličnega skoka, predstavlja polmer curka preden zadane površino, h' predstavlja pa višino gladine znotraj hidravličnega skoka na danem položaju r'.

Privzamemo, da se za majhen curek »razlije« s hitrostjo , ki je enaka hitrosti u v prejšnjem primeru, ko smo predpostavili neviskoznost tekočine.

Predpostavimo torej, da se curek »razlije«, kot da bi bil iz neviskozne tekočine, razen mejne plasti- plasti tekočine blizu vpadne površine, kjer na njeno obnašanje vplivajo učinki viskoznosti. Tok znotraj mejne plasti je viskozni laminarni tok, tok nad njim pa je laminarni tok, ki se giblje s hitrostjo . Velja, da se hidravlični skok razvije na mestu, kjer je debelina mejne plasti enaka višini vodne gladine.

Za izpeljavo formule predpostavimo, da je prej omenjena mejna plast le tanek del celotne debeline tekočine in da ostane tanka vse do trenutka hidravličnega skoka.

Če je povprečna hitrost toka pri danem polmeru, bo blizu mesta, kjer curek vpade na dno umivalnika . Velja še, da je hitrost med razvijanjem viskoznega sloja vedno manjša kot .

Na mestu hidravličnega skoka je , zato lahko zapišemo naslednjo neenakost:

Višino gladine h na mestu hidravličnega skoka pa lahko zapišemo kot:

Zapišimo še enačbi za volumski pretok in hitrosti in :

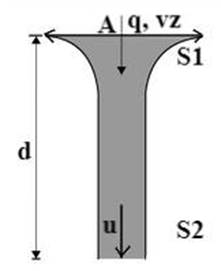
Shema toka curka iz pipe

Vemo, da z danim volumskim pretokom q skozi pipo premera A v času t kozarec napolnimo z m grami vode. Zapišimo še gostoto vode ρ= 997 in ploščino Zapišimo enačbo za masni pretok vode, prek nje pa zapišimo še povezavo med masnim in volumskim tokom q:

Hitrost ob izstopu curka iz pipe je torej:

Zapišemo še enačbo za hitrost curka u na razdaji d, z istim volumskim pretokom q in z izstopno hitrostjo . Sklepamo, da se tlak in tok s časom ne spreminjata.

Zapišemo enačbo hitrosti in kontinuitetno enačbo:

Nastavimo razmerje ploščin in :

oziroma