Hidravlični skok

V koritu: Teoretični pristop | Merjenje | Hipoteze | Rezultati | Ugotovitve

Napake dolžin padanja curka, radijev, premerov curka smo ocenili na 1mm natančno. Čase smo ocenili na 2s natančno, absolutna napaka kuhinjske tehtnice pa je 2g.

Naprej privzamemo še, da je, zaradi dolgotrajnosti izvedbe poskusa, med samim poskusom prihajalo do manjših razlik pretoka vode, kjer smo privzeli, da se pretok ne spreminja. Dopuščamo tudi možnost, da je prišlo do manjših napak pri dolžinskih meritvah, saj podlage nikoli niso bile naravnane popolnoma vodoravno. Pri slednjih lahko privzamemo, da so se v enaki meri pojavljale tekom vseh posameznih delov eksperimenta.

Najprej preverimo, da velja hipoteza, da je nastanek krožnega hidravličnega skoka neodvisen od vrste podlage:

[]	Material	d [cm]	R [cm]
12,7	Teflon	16,6	2
	plastika		2
	keramika		2
24,6	Teflon		2,5
	plastika		2,6
	keramika		2,5
43,3	Teflon		3,1
	plastika		3,1
	keramika		3,1
61,1	Teflon		4,4
	plastika		4,4
	keramika		4,4

Opazimo, da so, z izjemo meritve pri plastiki pri drugem sklopu meritev, radiji ob istem masnem pretoku in ob enaki dolžini d enaki, ne glede na vrsto podlage.

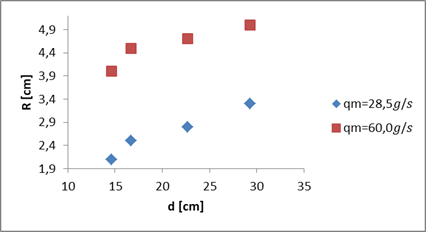
Preverimo še, če velja hipoteza, da se z višino d spreminja tudi R:

Zaradi lažje preglednosti narišemo kar

graf R(d) pri različnih vrednostih masnega pretoka :

Opazimo, da pri istem masnem pretoku qm z večanjem razdalje med pipo in podlago d, razdalja med robom curka in hidravličnim skokom R narašča.

Še več, opazimo, da se pri enakem d, a večjem qm poveča tudi R. Z »odpiranjem« pipe se torej poveča tudi radij hidravličnega kroga.

Nato podamo še meritve za primer, ko predpostavimo, da je tekočina neviskozna

N	Vrsta podlage	A [cm]	a [cm]	d [cm]	t [s]	m [kg]	q []	h [mm]	H [mm]	R [mm]
1	Aluminij	1,3	0,4	28,7	9,59	0,284	2,97	0,486	2,227	43,5
2			0,65		5,26	0,29	5,53	0,384	3,687	55
3			0,75		4,31	0,268	6,24	0,367	4,067	57,5
4			0,3		9,32	0,267	2,87	0,509	2,205	41,5
1	Plastika		0,4	27,7	8,89	0,274	3,09	0,671	2,723	31,5
2			0,3		9,72	0,293	3,02	0,579	2,474	36,5
3			0,6		6,77	0,269	3,99	0,797	3,828	26,5
4			0,7		4,92	0,27	5,50	0,423	3,849	50
1	Teflon		0,4	28,2	8,14	0,248	3,06	1,030	3,337	20,5
2			0,3		10,55	0,272	2,59	0,728	2,374	29
3			0,6		4,51	0,273	6,07	0,671	5,349	31,5
4			0,7	22,1	4,78	0,287	6,02	0,754	5,627	28
1	Keramika		0,2	24,9	11,62	0,243	2,10	0,939	2,186	22,5
2			0,4		7,61	0,28	3,69	0,587	3,041	36
3			0,5		6,88	0,284	4,14	0,542	3,278	39
4			0,7		4,13	0,278	6,75	0,503	5,151	42

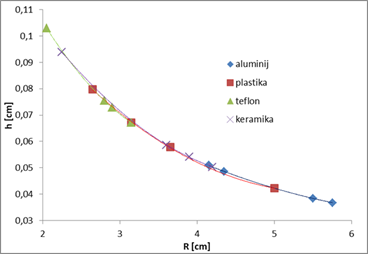
in narišemo pripadajoče grafe:

Graf h(R) višine vodne gladine v odvisnosti od polmera hidravličnega kroga:

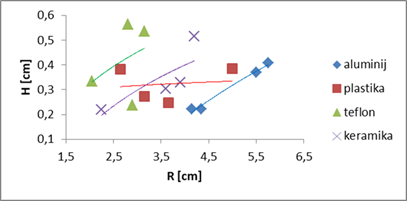
Graf H(R) višine vodne gladine po hidravličnem skoku v odvisnosti od polmera hidravličnega kroga:

Iz meritev opazimo, da velja poenostavitev v prvem delu teorije, ki pravi

Prav tako velja tudi, da se z večanjem volumskega pretoka q veča tudi R.

Drugi graf H(R) nam pri tem načinu računanja ne da nobenih pojasnil, iz grafa h(R) pa lahko razberemo, da z večanjem R višina gladine pred skokom h pada po skoraj enaki funkciji, ne glede na vrsto podlage. Pridemo do dveh sklepov:

a) Vrsta podlage ne igra vloge pri višini gladine vode pred hidravličnim skokom h,

b) Z večanjem volumskega pretoka q, se višina gladine h pred skokom manjša

Opomba: Če naredimo enake izračune z upoštevanjem, da a ni enak A, bo graf H(R) enak:

Graf H(R) višine vodne gladine po hidravličnem skoku v odvisnosti od polmera hidravličnega kroga, kjer predpostavimo, da a ni enak A:

Opomba: Pri meritvah smo upoštevali, da je tekočina neviskozna, debelina curka pa se med padcem spreminja.

Meritve za plastiko in teflon nam ne dajo nobenih pojasnil, zato se osredotočimo na meritve za aluminij in keramiko. Vidimo, da meritve za oba materiala ležijo na skoraj enakih krivuljah. Še več, ti krivulji sta podobni krivulji iz prejšnjega grafa h(R). Torej tudi za gladino vode po hidravličnem skoku pridemo do enakih sklepov.

Zapišemo še meritve za primer, ko predpostavimo, da imamo viskozno tekočino:

N	Material	r' [mm]	r [mm]	t [s]	q	[mm]	h [mm]	h' [mm]
1	Aluminij	27,69	45,50	0,0736	2,97	2,000	0,208	0,174
		22,50						0,207
		19,50						0,233
		15,00						0,291
		7,500						0,509
2		57,40	58,25	0,1124	5,53	3,250	0,366	0,181
		42,28						0,225
		37,985						0,245
		19,50						0,413
		13,00						0,565
3		38,76	61,25	0,164	6,24	3,750	0,322	0,256
		19,73						0,442
		8,800						0,806
		8,880						0,801
4		29,00	43,00	0,116	2,87	1,500	0,129	0,152
		21,50						0,200
		9,675						0,411
		4,000						0,833
1	Plastika	23,57	33,50	0,1245	3,09·	2,000	0,185	0,196
		18,60						0,242
		14,70						0,298
		2,600						1,071
1	Teflon	15,30	22,50	0,0735	3,06	2,000	0,281	0,287
		12,30						0,346
		3,200						0,939
		1,940						1,237
3	Keramika	25,36	41,50	0,10233	4,14	2,500	0,249	0,247
		23,30						0,266
		19,07						0,316
		15,40						0,378

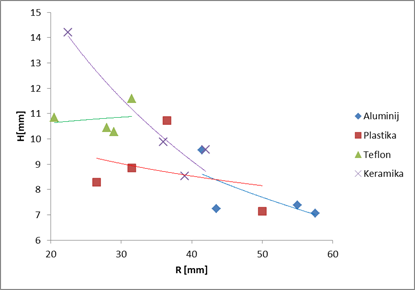
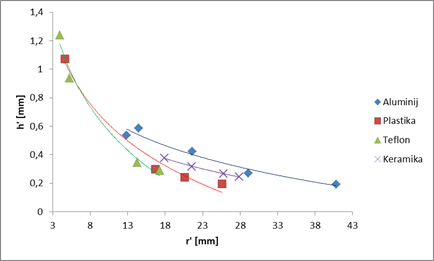
Spet narišemo graf. Tokrat rišemo graf h'(r'), kjer h' predstavlja višino gladine v točki, ko smo na oddaljenosti r' znotraj hidravličnega kroga. r' je razdalja od središča curka, do neke izbrane točke znotraj hidravličnega kroga.

Graf h'(r') višine gladine znotraj hidravličnega skoka na danem položaju r' v odvisnoti od tega položaja r', kjer smo predpostavili viskoznost tekočine:

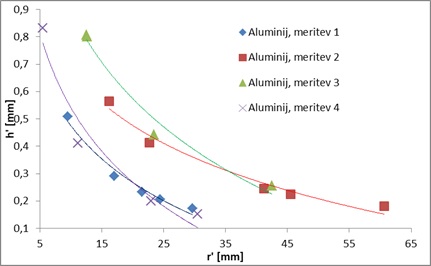
Opazimo, da nam tudi ta graf ne poda dovolj zadovoljivih rezultatov. Za vse podlage z naraščanjem r' h', torej, višina vodne gladine znotraj hidravličnega kroga, pada. Vendar pa za čedalje večje r' meritve ne tečejo po enakih krivuljah. Opazimo pa, da se pri pri meritvah, ko je , krivulje posameznih meritev začnejo prekrivati. Za zelo majhne r' bi torej lahko rekli, da je višina vodne gladine neodvisna od podlage.

Graf h'(r') višine gladine znotraj hidravličnega skoka na danem položaju r' v odvisnoti od tega položaja r', za primer aluminijeve podlage pri različnih masnih pretokih , kjer predpostavimo viskoznost tekočine:

Tudi tu opazimo sledeče:

Ko se oddaljujemo od curka, se niža tudi gladina vode. Podobno kot pri prejšnjih meritvah tudi tukaj meritve za posamezne poskuse ne ležijo na enaki krivulji.