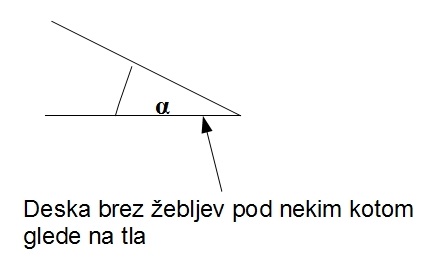
 Slika 2: Klanec.
Slika 2: Klanec.
Električni tok po prevodnikih, za katere velja Ohmov zakon, lahko ponazorimo s poševno desko, posejano z žeblji(slika 3), po kateri spuščamo kroglice. Med trkoma se gibljejo kroglice enakomerno pospešeno, ob trku z žebljem izgubijo pridobljeno kinetično energijo in informacijo o gibanju pred trkom. Posledica tega je v povprečju enakomerno gibanje po klancu.
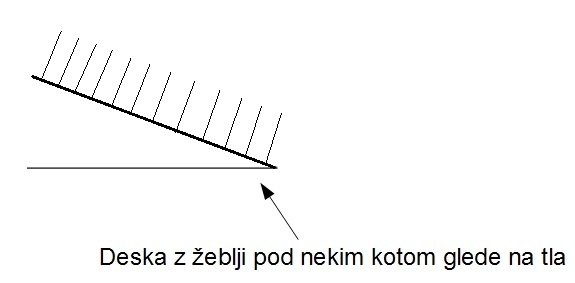 Slika 3: eblji na klancu.
Slika 3: eblji na klancu.
Mehanizem električnega upora lahko torej pojasnimo s trki nosilcev električnega naboja v prevodni snovi. Ta model je leta 1900 predstavil Paul Drude.
V prevodnem kanalu, kjer je električno polje E (v našem eksperimentu ponazorjen z naklonom deske), so nosilci naboja prosti elektroni (ogice). Na vsakega od njih deluje sila FE = -eE, zaradi katere bi se moral elektron gibati pospešeno:
ma=FE =-eE,
kjer je m masa elektrona, a pospešek, FE sila, ki deluje nanj, e naboj elektrona in E električna poljska jakost. Pospeevalna sila v naem sistemu, ki je ekvivalentna e*E, je dinamična komponenta sile tee. Le-ta je sinusno odvisna od naklonskega kota podlage.
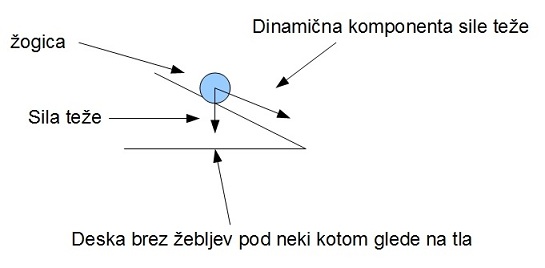 Slika 4: oga na klancu.
Slika 4: oga na klancu.
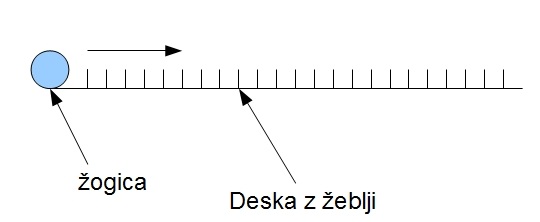 Slika 5: Deska na tleh.
Slika 5: Deska na tleh.Ker pa v našem primeru prihaja do trkov z ostalimi delci v snovi (žeblji), elektron izgubi del hitrosti in s tem tudi del kinetične energije, kar spominja na neelastični trk. Tako izrinjen elektron začne zaradi sile FE = -eE ponovno pospeševati do novega trka. Ta situacija se ponavlja (glej posnetek), zato je bolje govoriti o poprečni hitrosti elektrona oziroma o povprečni hitrosti vE celotne množice prostih elektronov (ki jo primerjamo z električnim tokom). V modelu predpostavimo povprečno silo upora Fu=-kvE.
Dobimo gibalno enačbo (v poprečju enakomernega gibanja) prostega elektrona, katerega poprečni pospešek a je 0:
ma=FU +FE =-kvE - eE,
a=(-kvE -eE)/m=0 => kvE /m = (-eE)/m,
Konstanta k / m = f v modelu trkov predstavlja oceno o frekvenci trkov, njej obratna vrednost τ = 1 / f pa čas med zaporednima trkoma.
Iz zgornje enačbe dobimo:
vE = (-eEτ)/m ,
iz česar lahko razberemo, da je povprečna hitrost prostih elektronov sorazmerna električni poljski jakosti.
Če upoštevamo še da je gostota električnega toka J = ρvE in ρ=-ne, kjer pomeni n število prostih elektronov v m3 snovi, potem je:
vE =J/(-ne) = (-eEτ)/m => J= (ne2 Eτ)/m .
Tako pridemo do enačbe, ki povezuje vektor gostote toka in vektor poljske
jakosti. Sorazmernostni faktor imenujemo specifična električna prevodnost: γ=ne2τ/m. Ta enačba je ena izmed najpomembnejih spoznanj Drudejevega modela.
Posnetek 1: Drudejev model.