MODEL
1. Eksperiment
Če pri prvem eksperimentu dogajanje obravnavamo kot vsiljeno nihanje (zgornje nihalo upoštevamo samo kot zunanji pospešek) lahko izpeljemo funkcijo:
$$ f(x) = (U - \frac{A \omega^2}{m \omega^2 - k} sin(\omega \frac{\pi}{2} \sqrt{\frac{m}{k}}))sin(\sqrt{\frac{m}{k}} x) + \frac{A \omega^2 sin(\omega x)}{m \omega^2 -k},$$kjer je U odmik nihala po \( \frac{\pi}{4} \), A pospešek zgornjenega nihala, m masa uteži, k koeficient vzmeti, \( \omega \)
krožna frekvenca vzbujanja.
Sicer nam funkcija predlaga, da v primeru dveh vzmetnih nihal zunanji pospešek na nihajni čas ne vpliva.
Kot kažejo rezultati, se nihajni čas nihala, ki ga vzbuja sinusno nihanje, res ne spremeni oziroma so spremembe neznatne tj. manjše od napake.
To najlažje razložimo tako, da si predstavljamo nihalo, ki ga vzbujamo z zelo veliko oziroma zelo majhno frekvenco.
V tem primeru bo vzbujanje pospešilo nihalo, kmalu zatem pa ga z nasprotno enakim učinkom upočasnilo.
Tako bo na periodi enega nihaja veljalo, da je povprečen pospešek enak nič.
Z GeoGebro lahko dobimo funkcijo z različnimi parametri, da si lažje predstavljamo. Vidimo, na primer da je pri \(A = 0\), torej ko ni pospeška nihanje popolnoma sinusno.
2. Eksperiment
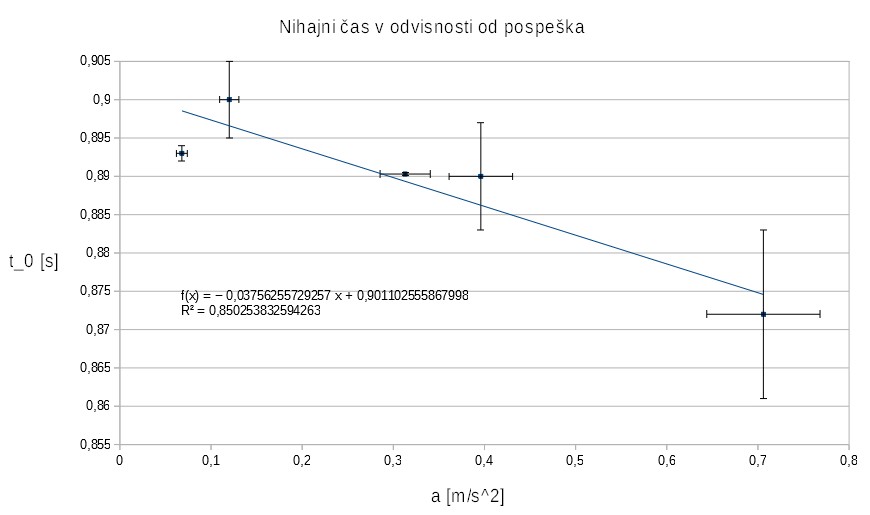
Graf nihajnega časa v odvisnosti od pospeška \(t_0(a)\)
Iz grafa je videti, da nihajni čas linearno pada s pospeškom sistema. Poleg tega lahko iz presečišča grafa z y osjo lahko razberemo koliko je \(t_0\) v nepospešenem sistemu in ali se ujema s predvideno vrednostjo lastnega nihanja. \(t_{0_i} = 901 \pm 135 ms\) (napaka dobljena iz fita) primerjamo s \(t_{0} = 956 \pm 5 ms\) in vidimo, da se podatka ujemata, tako da tudi fit ni tako slab.
Če si sicer pogledamo formulo $$ \omega = \sqrt{\frac{g+a}{l}},$$ (ki sledi iz enačbe 8), ne bi pričakovali linearne funkcije. Če pa jo narišemo dobimo:
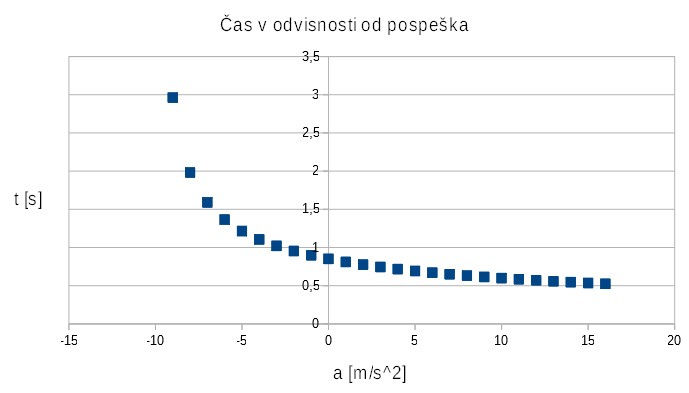
Očitno je prava formula potenčne oblike, a je za a>0 sicer zelo podobna linearni funkciji.
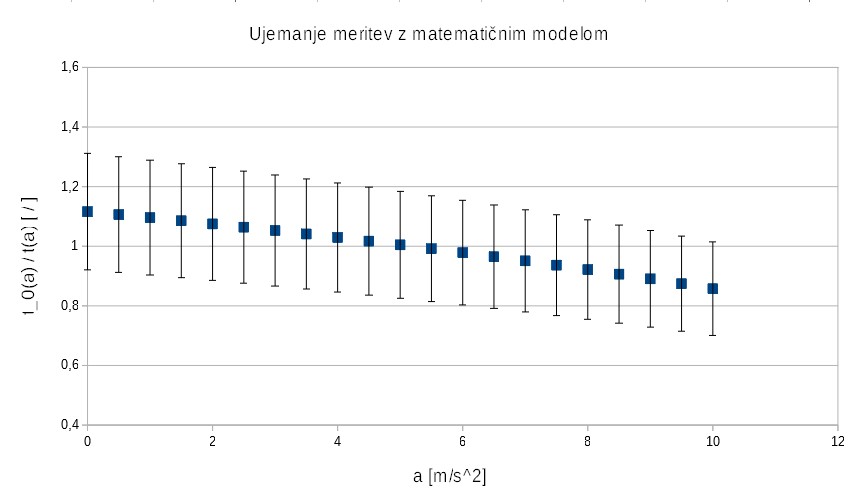
Če primerjamo naše meritve z matematičnim modelom, tako da dobljene vrednosti pri danih pospeških delimo med sabo, dobimo graf, ki nam pokaže, kako dobro se meritve ujemajo z matematičnim modelom. Če je vrednost grafa 1 to pomeni, da je ujemanje popolno. Pri pospeških od 0 do 10 vidimo, da to z upoštevanjem napake drži. Sicer so naše meritve potekale pri nižjih pospeških od 0 do 1 ms-2, tako da bi za bolj natančno oceno zagotovo meritve morali opraviti pri večjem razponu pospeškov.
Sklep
V V pospešenem sistemu se z nihali zgodi naslednje: nihajni čas se pribiližno linearno zmanjšuje v odvisnosti od pospeška sistema, kot opazimo v 2. eksperimentu. Če je povprečje pospeška enak nič, pa se efekt izniči in se nihalu nihajni čas ne spremeni, kot je razvidno iz prvega eksperimenta. Morda je mogoče, da v primeru dveh sklopljenih matematičnih nihal seštevek pospeškov ni natanko nič in bi prišlo, do kakšnega efekta, ampak tega ne moremo preveriti zaradi trackerja.