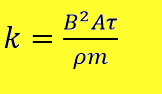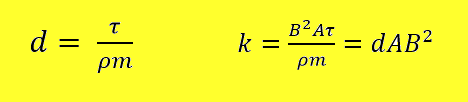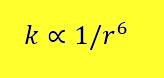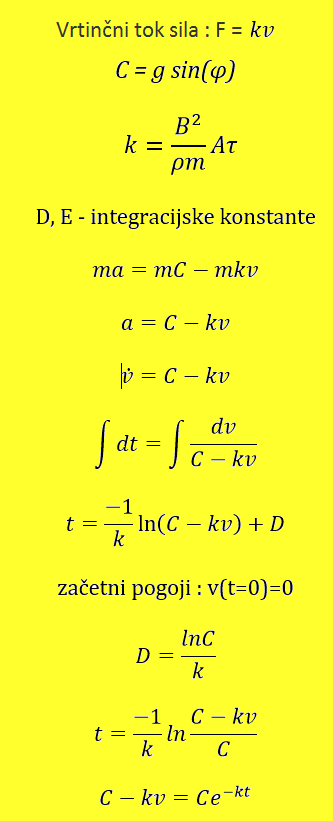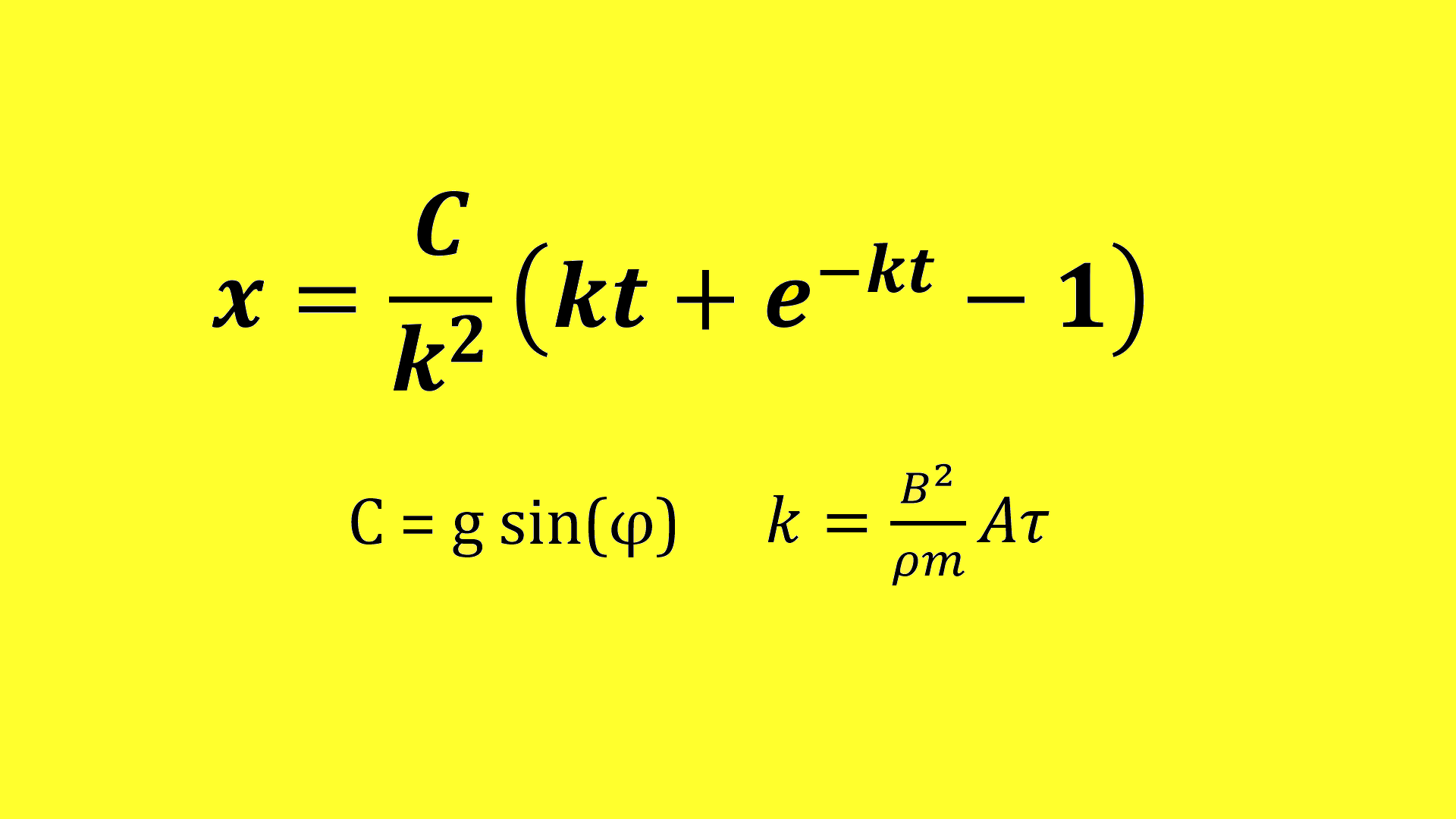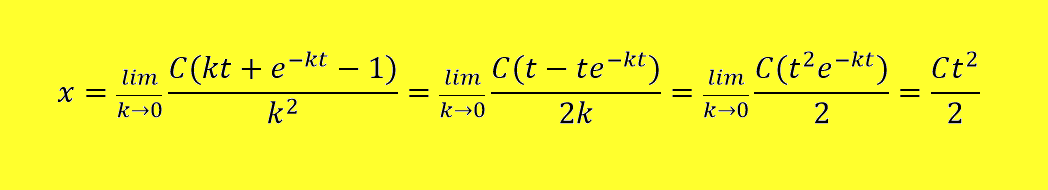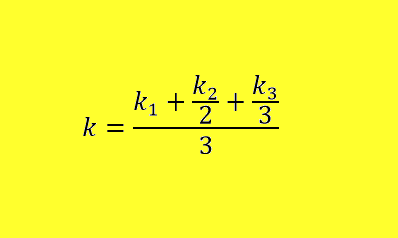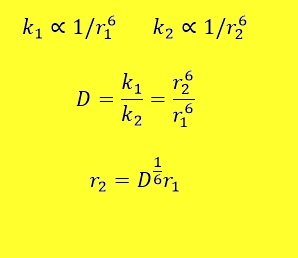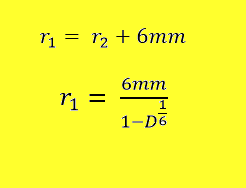|
Rezultate
eksperimenta smo ob koncu projektnega dela Magnetno zaviranje na klancu
poskušali pojasniti z matematičnim modelom. Na podlagi
teoretskega znanja, ki smo ga dobili s študijem fizike ter izkustvenega znanja,
pridobljenega ob pripravi in izvajanju eksperimenta, smo v skupini menili, da
je razlog za magnetno zaviranje vozička na klancu v vrtinčnem toku. Vrtinčni tok so
zanke električnega toka, inducirane v prevodniku zaradi spreminjajočega se
magnetnega polja. Pred magnetom se, v smeri njegovega gibanja po prevodniku,
gostota magnetnega polja magneta povečuje. To povzroči indukcijo vrtinčnega
toka.
Za magnetom, v
nasprotni smeri gibanja magneta, pa se gostota magnetnega polja magneta
zmanjšuje. To spet povzroči indukcijo vrtinčnega toka, a v nasprotni smeri kot teče
prvi vrtinčni tok.
Gre za posledico
Faradayevega zakona o indukciji.
Vrtinčni tok pa
ustvarja svoje magnetno polje, ki nasprotuje spreminjanju začetnega magnetnega
polja premikajočega se magneta, ki je povzročil nastanek vrtinčnega toka. To
pojasnjuje Lenzov zakon.
Zaradi tega
nasprotovanja spreminjanju magnetnega polja (spreminja se zaradi premikanja
vozička), nastane sila, ki deluje v nasprotni smeri premikanja vozička.
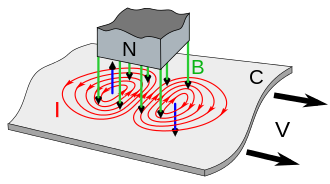
Slika št. 10: Prikaz vrtinčnega
toka
N - magnet
B (zelena barva) - začetno magnetno polje magneta
I (rdeča barva) - zanke vrtinčnega toka
C – prevodnik, ki se premika
V - smer premikanja prevodnika
puščice (modra barva) – magnetno polje, ki ga ustvari vrtinčni tok, ki
nasprotuje spreminjanju začetnega magnetnega polja premikajočega se
magneta
Poleg vrtinčnega toka pa na
premikanje vozička po klancu vplivajo tudi sila gravitacije ter sila trenja.
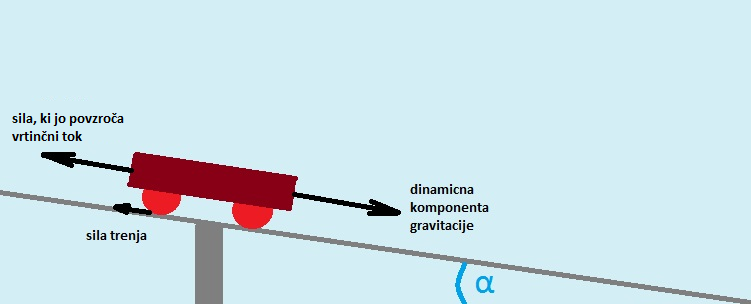
Slika št. 11: Prikaz delovanja sil na voziček
V eksperimentih
smo uporabili različne postavitve magnetov na vozičku. Za lažjo predstavo smo
izdelali enostavno sliko, ki kaže te različne postavitve. 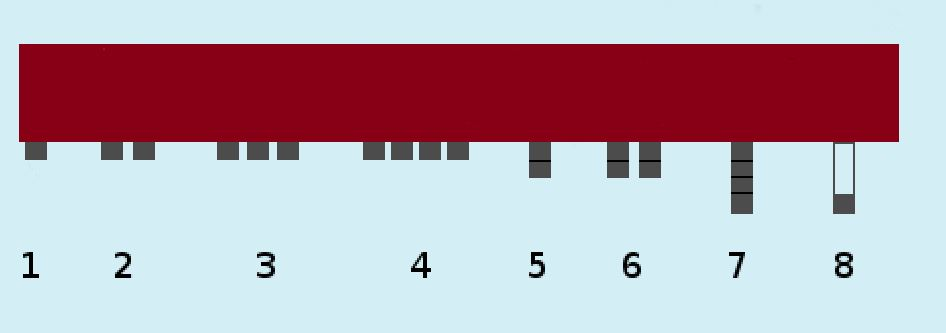
Slika št. 12: Prikaz
različnih postavitev magnetov na vozičku (magneti so bili vedno postavljeni zaporedno torej v eni vrsti)
1 - 1 magnet tik ob
vozičku
2 - 2 magneta tik ob
vozičku
3 - 3 magneti tik ob
vozičku
4 - 4 magneti tik ob
vozičku
5 - 2 magneta, postavljena
drug na drugem
6 - 2 krat po 2 magneta,
postavljena drug na drugem
7 - 4 magneti, postavljeni
drug na drugem
8 - 1 magnet, s plastiko
smo simulirali razdaljo 3 magnetov od vozička
Sivi kvadratki – magneti
Rdeča barva - voziček
Enačba matematičnega modela
Pri
izračunu gibanja vozička na klancu smo uporabili Newtonov zakon. Z reševanjem diferencialnih enačb smo prišli do
končne enačbe (izpeljava je prikazana na koncu), ki prikaže razmerje med
pozicijo vozička (x) ter časom (t) premikanja vozička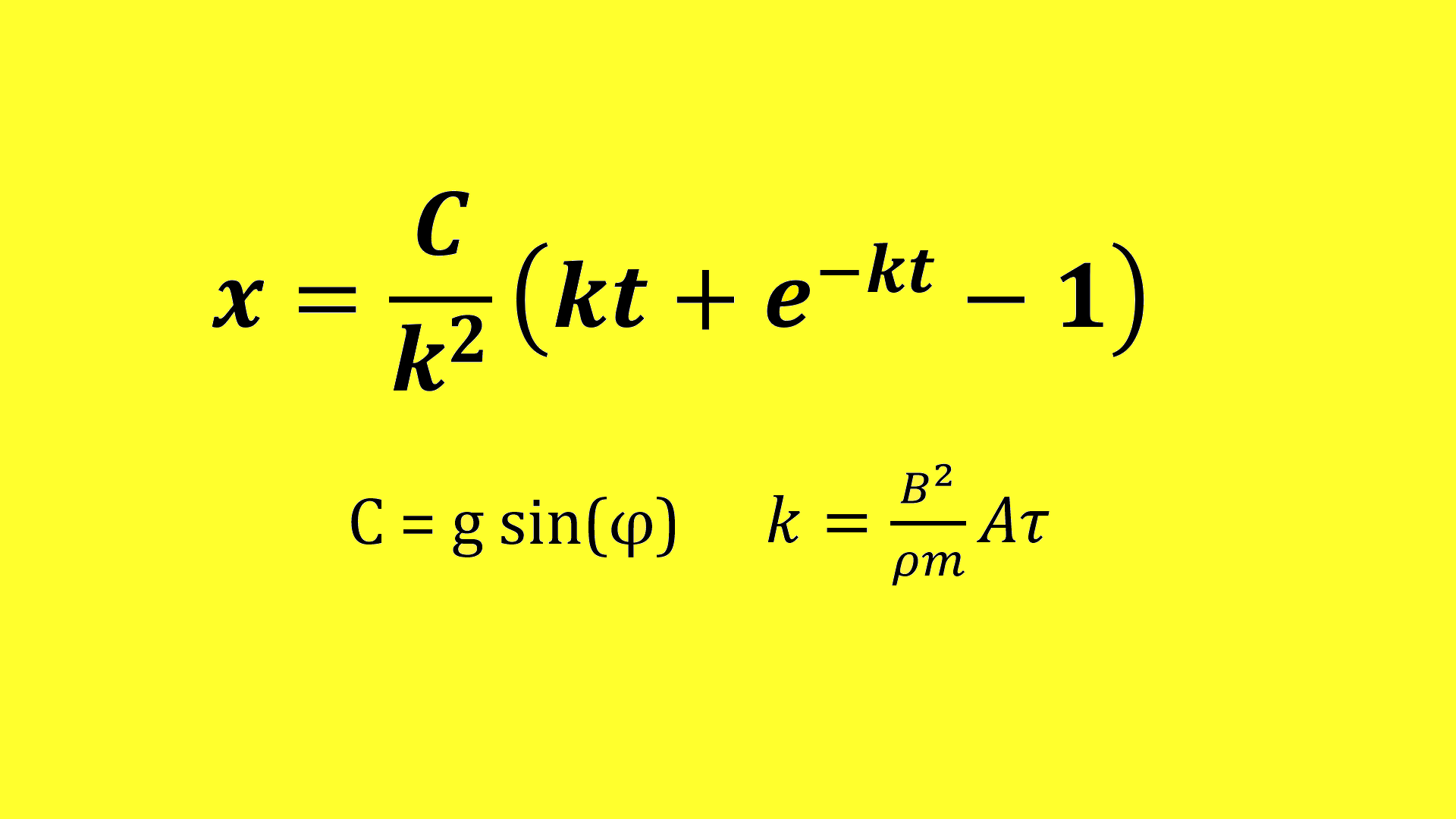
φ – kot klanca
t – čas
x –pozicija
τ – širina prevodnika
m –masa prevodnika
ρ – upornost
B –magnetno polje
A – površina magneta
Primerjava matematičnega
modela z meritvami Da bi lahko ovrednotili matematični model, smo ga želeli primerjati z
meritvami oziroma rezultati eksperimenta. Vse meritve prikazuje graf št. 12. 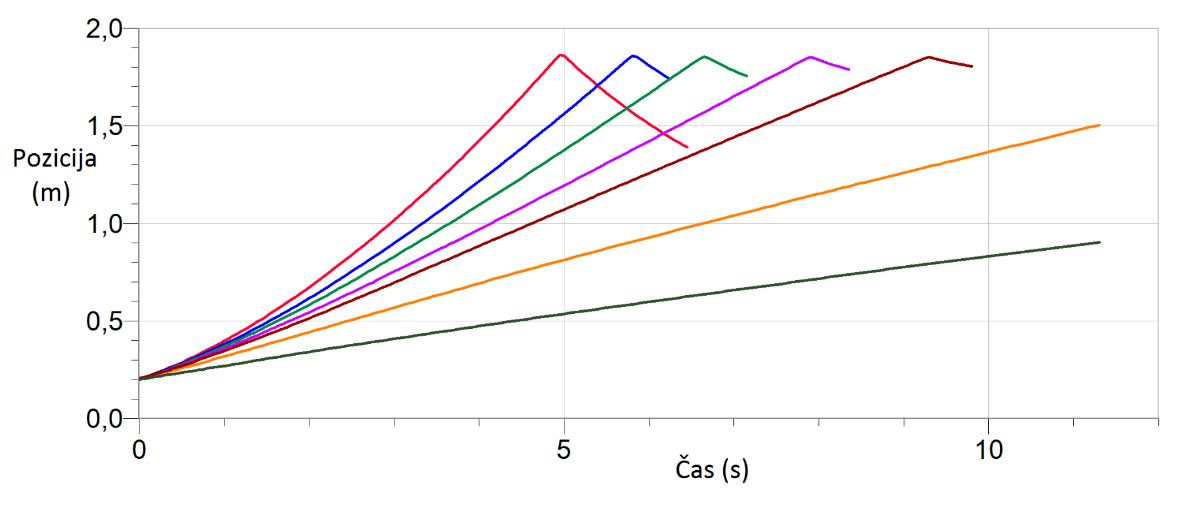
Slika št. 13: Graf – primerjava hitrosti in
pozicije vozička pri določenih parametrih in kotu 0.86░
rdeča krivulja –
voziček brez magnetov
modra krivulja –
1 magnet tik ob vozičku
rjava krivulja –
4 magneti tik ob vozičku
oranžna krivulja
– 2 magneta, postavljena drug na drugem
zelena krivulja –
2 magneta tik ob vozičku
vijolična
krivulja – 3 magneti tik ob vozičku
temno zelena
krivulja – 2 krat po 2 magneta, postavljena drug na drugem
Naslednji korak je bila izdelava grafov, ki prikazujejo matematični model
ter meritve. S tem bi bila primerjava najboljša. Uporabili smo program GnuPLot,
s katerim smo meritve prilagodili (v nadaljevanju fitali) in s tem dobili
realne koeficiente. Z njimi smo lahko izdelali grafične prikaze primerjav za
posamezne meritve.
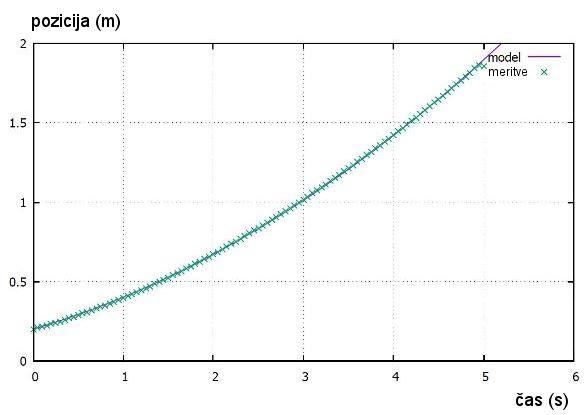
Slika št. 14: Graf – prilagoditev (fit) krivulje
meritvam pri vozičku brez magnetov (rdeča krivulja na sliki št. 13) V matematičnem modelu imamo dva poglavitna koeficienta: k in C. Koeficient
k vsebuje parameter gostote magnetnega polja B. V primeru, ko na vozičku ni
pritrjenih magnetov, je vrednost k = 0. Da bi dobili končno enačbo vozička brez
magnetov, smo uporabili L'H˘pitalovo pravilo. 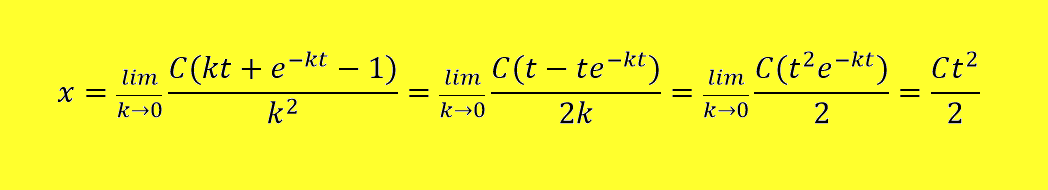
Tako smo dobili koeficient C, katerega vrednost je 0.06906.
Z dobljenim koeficientom C smo nato želeli pogledati, kako bi s fitanjem
koeficienta k matematični model primerjali z meritvami. Za primerjavo smo
izrisali tri grafe:
- fit meritev pri vozičku z enim magnetom (modra krivulja na sliki št. 13);
- fit meritev pri
vozičku z dvema magnetoma tik ob vozičku (zelena krivulja na sliki št. 13);
- fit meritev pri
vozičku s tremi magneti tik ob vozičku (vijolična krivulja na sliki št. 13). 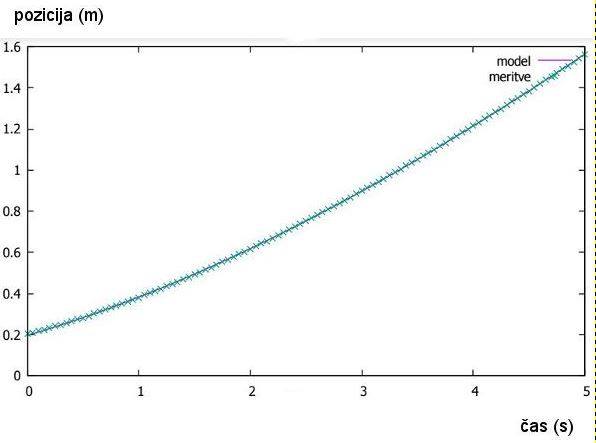
Slika št. 15: Graf –
prilagoditev (fit) krivulje meritvam pri vozičku z enim magnetom, z vrednostjo
k1 = 0.07595 (modra krivulja na sliki št. 13) 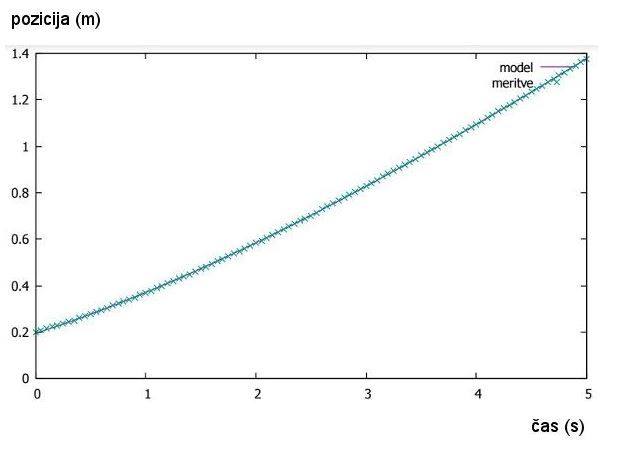
Slika št. 16: Graf – prilagoditev (fit)
krivulje meritvam pri vozičku z dvema magnetoma tik ob vozičku, z vrednostjo k2
= 0.1294 (zelena krivulja na sliki št. 13)
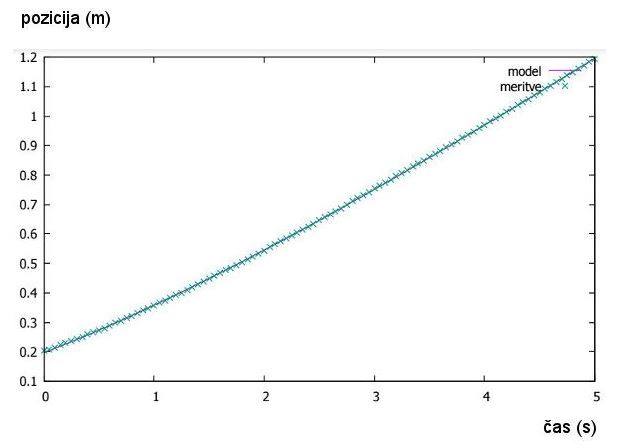
Slika št. 17: Graf – prilagoditev (fit)
krivulje meritvam pri vozičku s tremi magneti tik ob vozičku z vrednostjo k3
= 0.1948 (vijolična krivulja na sliki št. 13)
Izrisani grafi so pokazali, da se matematični model lepo prilega meritvam.
Sklepali smo lahko, da sta zaradi tega ujemanja, matematični model ter njegov
izračun verjetno pravilna. S tem smo dosegli prvotni cilj, ki je bil potrditi
ali ovreči matematični model.
Koeficient k v
matematičnem modelu
V matematičnem modelu sta dve konstanti: C in k. Konstanta C je povsem
jasna, v zvezi z konstanto k pa se nam je porodilo nekaj vprašanj, o katerih
razmišljamo v nadaljevanju.
Pri fitanju smo opazovali koeficient k, ko gre za voziček z enim magnetom
(modra krivulja na sliki št. 12), z dvema magnetoma tik ob vozičku (zelena
krivulja na sliki št. 12) ter s tremi magneti tik ob vozičku (vijolična
krivulja na sliki št. 12). Dobili smo naslednje vrednosti koeficienta k:
- 1 magnet tik ob vozičku, k1 = 0.07595,
- 2 magneta tik ob vozičku, k2 = 0.1294,
- 3 magneti tik ob vozičku, k3 = 0.1948.
Ugotovili smo, da našteti koeficienti približno izkazujejo nek vzorec, saj
je k2= 2k1, k3=3k1 ter k3=(3/2)k2 (tukaj bi morali bit znaki za približno enako).
Zaradi te ugotovitve smo naredili povprečje k1, k2 in k3. 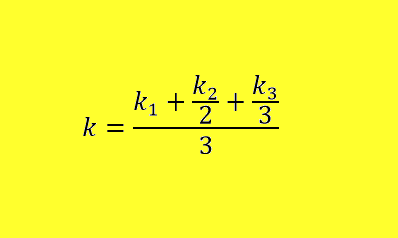
To povprečje znaša k = 0.07103. Nato smo grafe še enkrat izrisali z novo
vrednostjo k = 0.07103 ter k1 = k, k2 = 2k in k3
= 3. 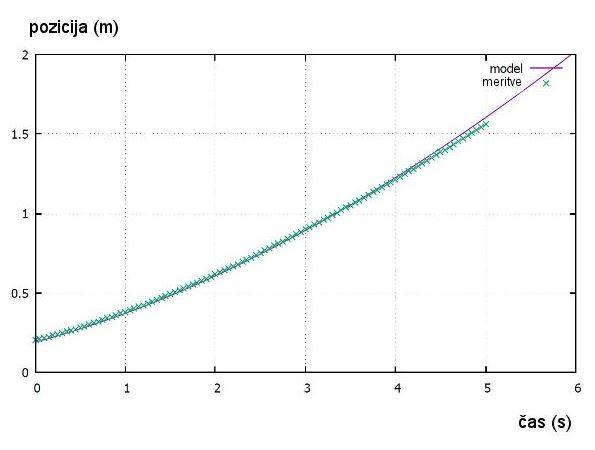
Slika št. 18: Graf –
primerjava meritev in matematičnega modela s povprečno vrednostjo k1
= 0.07103 (voziček z enim magnetom - modra krivulja na sliki št. 13) 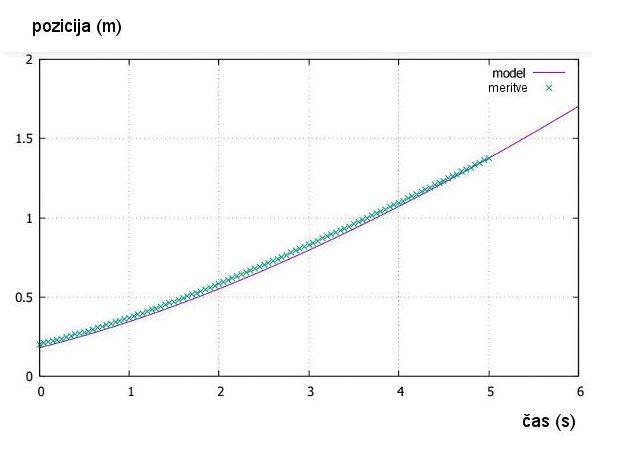
Slika št. 19: Graf –
primerjava meritev in matematičnega modela s povprečno vrednostjo
k2 = 2*0.07103
= 0.14206 (voziček z dvema magnetoma tik ob vozičku - zelena krivulja na sliki
št. 13) 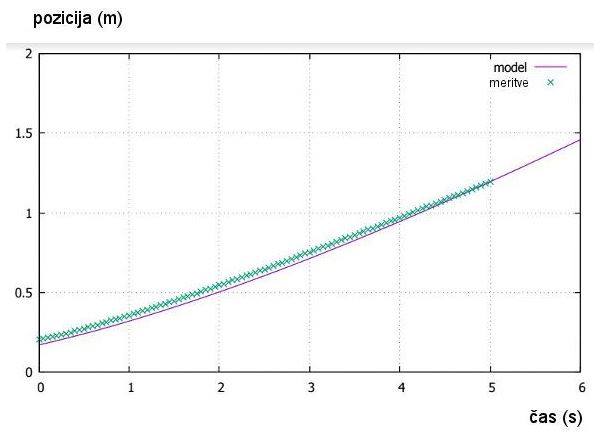
Slika št. 20: Graf –
primerjava meritev in matematičnega modela s povprečno vrednostjo k3
= 3*0.07103 = 0.21309 (voziček s tremi magneti tik ob vozičku – vijolična
krivulja na sliki št. 13)
Veliko boljši pokazatelj, da so meritve izkazovale nek
vzorec, je primerjava povprečnega k s k1, k2/2 in k3/3.
To smo poskušali prikazati na naslednjem grafu.
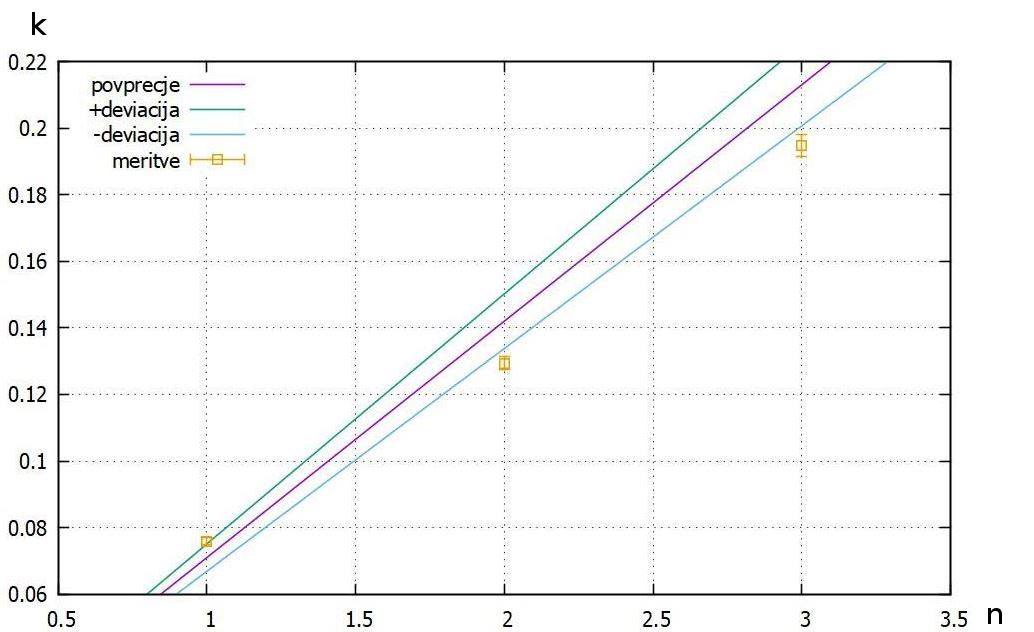
Slika št. 21: Graf –
prikaz posameznih vrednosti k1, k2 in k3 ter
premice n*k
premica vijolične barve - n*k
premica zelene barve - n*(k+deviacija)
premica modre barve – n*(k-deviacija)
rumeni kvadratki – fitane vrednosti k (k1, k2 in k3)
rumeni repi kvadratkov – napake fitanih vrednosti k (k1, k2
in k3)
Pri fitanju je program poleg vrednosti izračunal tudi napako vrednosti k in
sicer:
k1 = 0.07595 ▒
0.001125
k2 = 0.1294 ▒ 0.00204
k3 = 0.1948 ▒ 0.0032178
Vrednost deviacije je 0.004.
Za izračun povprečja k smo uporabili le tri fitane vrednosti k. Zato je
deviacija povprečja pomemben faktor in dodali smo jo na grafu kot dve premici (zelena
in modra barva premice).
V grafu je razvidno, da se intervali fitanih k (k1, k2
in k3) in deviacij ▒ ne
pokrivajo najbolje.
Poleg teh napak, ki jih je izračunal program, so bile v eksperimentih
narejene še napake pri merjenju. Odločili smo se, da bi naredili še en graf,
kjer bi upoštevali napake meritev na vrednost fitanih k (k1, k2
in k3). 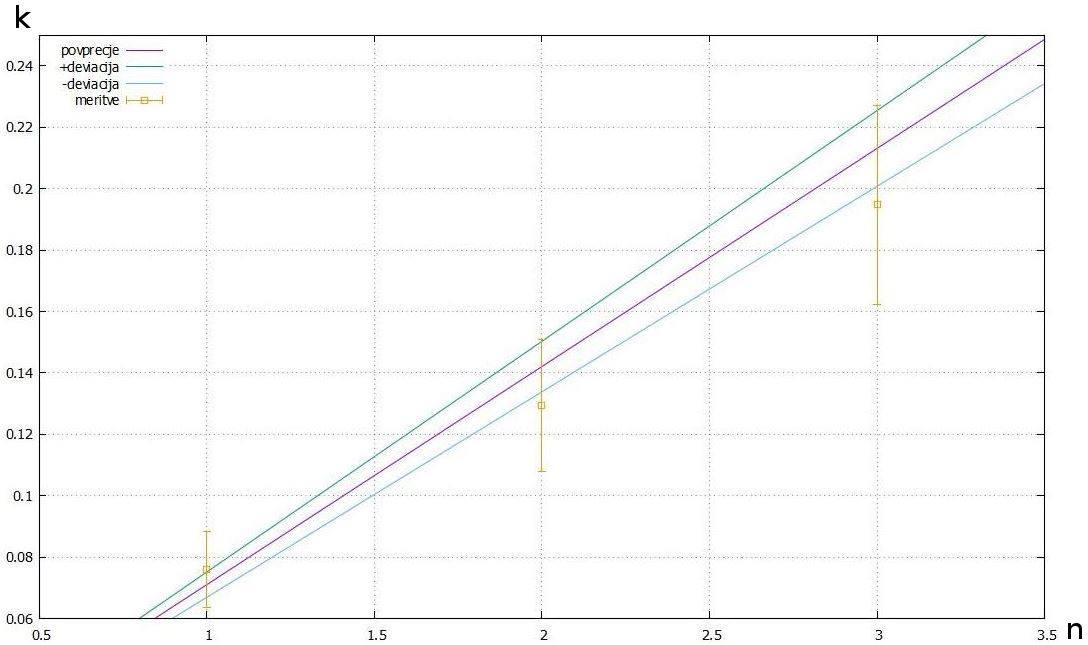
Slika št. 22: Graf –
prikaz posameznih vrednosti k1, k2 in k3 ter
premice n*k, z upoštevanimi napakami meritev
premica vijolične barve - n*k
premica zelene barve - n*(k+deviacija)
premica modre barve – n*(k-deviacija)
rumeni kvadratki – fitane vrednosti k (k1, k2 in k3)
rumeni repi kvadratkov – napake fitanih vrednosti k (k1, k2
in k3), z upoštevanimi napakami meritev
Napake fitanih vrednosti k (k1, k2 in k3)
z napakami meritev:
k1 = 0.07595 ▒ 0.012517
k2 = 0.1294 ▒ 0.0214566
k3 = 0.1948 ▒ 0.03244
Vrednost deviacije je 0.004
Za napake meritev smo uporabili ocenjeno vrednost napak v poglavju Napake
(projektna naloga Magnetno zaviranje na klancu). Ocenjena vrednost napak
meritev je bila približno 15%.
V grafu je razvidno, da se intervali napak k tokrat pokrivajo z deviacijo
povprečja. Zavedamo se, da je graf ne prikazuje povsem realnih rezultatov, ker
je šlo pri vrednosti napak meritev zgolj za oceno. Vseeno pa smo menili, da ti
rezultati nakazujejo vzorec in zato bomo naredili isti postopek še z drugimi
meritvami, ki smo jih tudi naredili v eksperimentih.
Model se je torej ob povprečni vrednosti k ter k2 = 2k in k3
= 3k (ko so bili magneti tik ob vozičku)
dokaj dobro ujemal z meritvami. Zato smo naredili še dva grafa, ki bi to dodatno
potrdila. Zanimalo nas je namreč, ali bi se ta vzorec (k2 = 2k1
in k3 = 3k1) ponovil, če bi uporabili meritve vozička z magneti drug na drugem.
Ponovno smo fitali meritve. Pri fitanju smo dobili koeficient k, ko gre za
voziček z dvema magnetoma drug na drugem (oranžna krivulja na sliki št. 13) in
z dvakrat dvema magnetoma drug na drugem (temnozelena krivulja na sliki št. 13).
Dobili smo naslednje vrednosti koeficienta k: k1 = 1.02505 ter k2
= 2.00922. Ponovno smo izračunali povprečno vrednost k = 1.01483 in izrisali
grafa z uporabo te povprečne vrednosti. 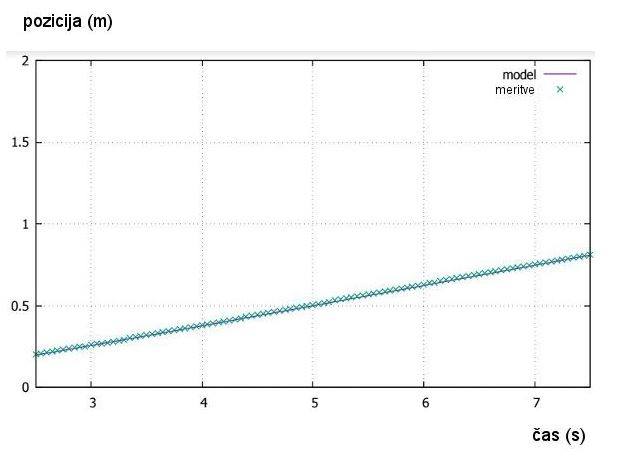
Slika št. 23: Graf –
primerjava meritev in matematičnega modela s povprečno vrednostjo k1
= 1.01483 (voziček z dvema magnetoma drug na drugem – oranžna krivulja na sliki
št. 13) 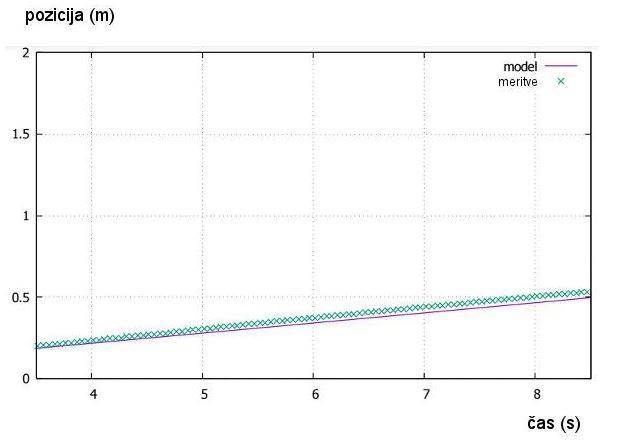
Slika št. 24: Graf –
primerjava meritev in matematičnega modela s povprečno vrednostjo k2
= 2*1.01483 = 2.02966 (voziček z dvakrat dvema magnetoma drug na drugem – temno
zelena krivulja na sliki št. 13)
Ponovno smo tudi za te meritve želeli prikazati primerjavo
povprečnega k s k1 in k2/2. Zato smo ponovno naredili dva
grafa.
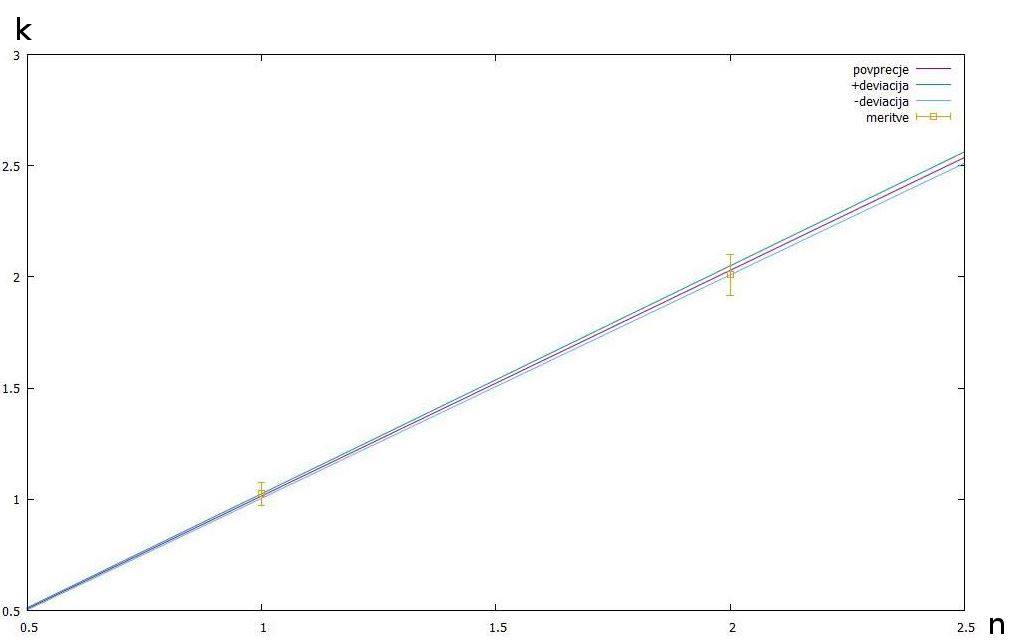
Slika št. 25: Graf –
prikaz posameznih vrednosti k1 in k2 ter premice n*k
premica vijolične barve - n*k
premica zelene barve - n*(k+deviacija)
premica modre barve – n*(k-deviacija)
rumeni kvadratki – fitane vrednosti k (k1 in k2)
rumeni repi kvadratkov – napake fitanih vrednosti k (k1 in k2)
Napake fitanih vrednosti k (k1 in k2):
k1 = 1.02505 ▒ 0.05117
k2 = 2.00922 ▒ 0.091291
Vrednost deviacije je 0.01.
Tokrat se napake fitanih vrednosti k in deviacije povprečja dobro ujemajo.
Ker pa smo imeli le dve meritvi, smo se zavedali, da so zaradi tega rezultati
nepopolni. Če bi imeli več meritev, bi bilo ujemanje prikazanih vrednosti bolj
prepričljivo. Enako kot pri prejšnji meritvah (magneti tik ob vozičku) smo tudi pri teh
dveh meritvah (magneti, postavljeni drug na drugem), naredili še en graf, v
katerem smo prikazali primerjavo fitanih vrednosti k (k1
in k2) z upoštevanimi napakami meritev. 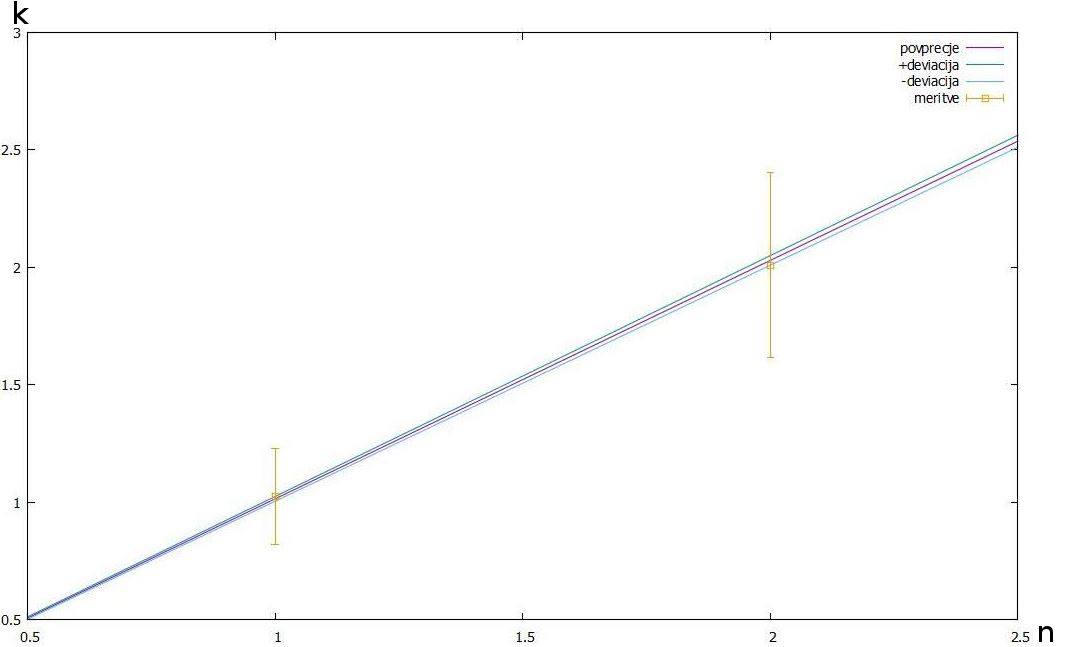
Slika št. 26: Graf –
prikaz posameznih vrednosti k1 in k2 ter premice n*k, z upoštevanimi napakami
meritev
premica vijolične barve - n*k
premica zelene barve - n*(k+deviacija)
premica modre barve – n*(k-deviacija)
rumeni kvadratki – fitane vrednosti k (k1 in k2)
rumeni repi kvadratkov – napake fitanih vrednosti k (k1 in k2),
z upoštevanimi napakami meritev
Napake fitanih vrednosti k (k1 in k2) z napakami meritev:
k1 = 1.02505 ▒ 0.205
k2 = 2.00922 ▒ 0.3927
Vrednost deviacije je 0.01. Zadnja dva grafa sta nakazala, da se vzorec (k2 = 2k1)
iz prejšnjih grafov ponavlja. Namreč, ko magnetoma, ki sta drug na drugem
(koeficient k1), dodamo še dva magneta, ki sta prav tako drug na
drugem (koeficient k2), se k prvih dveh magnetov pomnoži z 2. Torej:
k2 =2k1.
Zaradi te ugotovitve, smo si ponovno pogledali formulo
k, ki je:
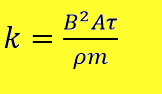
Vse vrednosti, ki se pri različnih meritvah ne
spreminjajo, smo združili v:
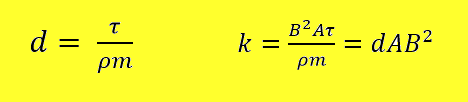
Edini vrednosti, ki sta se pri meritvah vozička na klancu spreminjali, sta
gostota magnetnega polja (B) in površina magneta (A). Na spreminjanje vrednosti
k pri naših meritvah je lahko vplivala le površina magnetov (A), le gostota
magnetnega polja (B) ali pa obe vrednosti naenkrat.
Izhodišče je, da je k2 = 2k1. Ko smo
izmerili k2, je bilo na vozičku dvakrat več magnetov (tik ob
vozičku) kot pri meritvah, ki so nam dale vrednost k1. Površina dveh
magnetov je dvakrat večja od površine enega magneta. Na podlagi obeh trditev
smo sklepali, da je na naše meritve najverjetneje vplivala površina magneta
(A).
Menili smo, da bi bilo v naslednjem koraku dobro pogledati, kako je z
vplivom gostote magnetnega polja (B) na vrednost k.
Iz pridobljenega znanje fizike vemo, da je gostota magnetnega polja (B) magnetnega
dipola obratno sorazmerna z razdaljo na kubik (r3). To bi pomenilo,
da je k obratno sorazmeren z razdaljo s potenco 6 (r6).
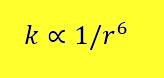
Hoteli smo izvedeti, ali je mogoče zaznati to sorazmernost v naših
meritvah. Odločili smo se, da pogledamo konstanto k pri naslednjih dveh
meritvah:
- voziček z enim magnetom tik ob vozičku,
- voziček z enim magnetom na razdalji 3 magnetov od vozička (razdaljo smo
dosegli z uporabo plastičnih koščkov).
Opomniti velja, da so bile meritve, ki bodo predstavljene v nadaljevanju,
opravljene na drugem vozičku, ki smo ga uporabili na začetku, potem pa smo ga
zamenjali z bolj ustreznim. Zaradi tega bo vrednost k različna od te, ki je
bila uporabljana v prejšnjih poglavjih poročila.
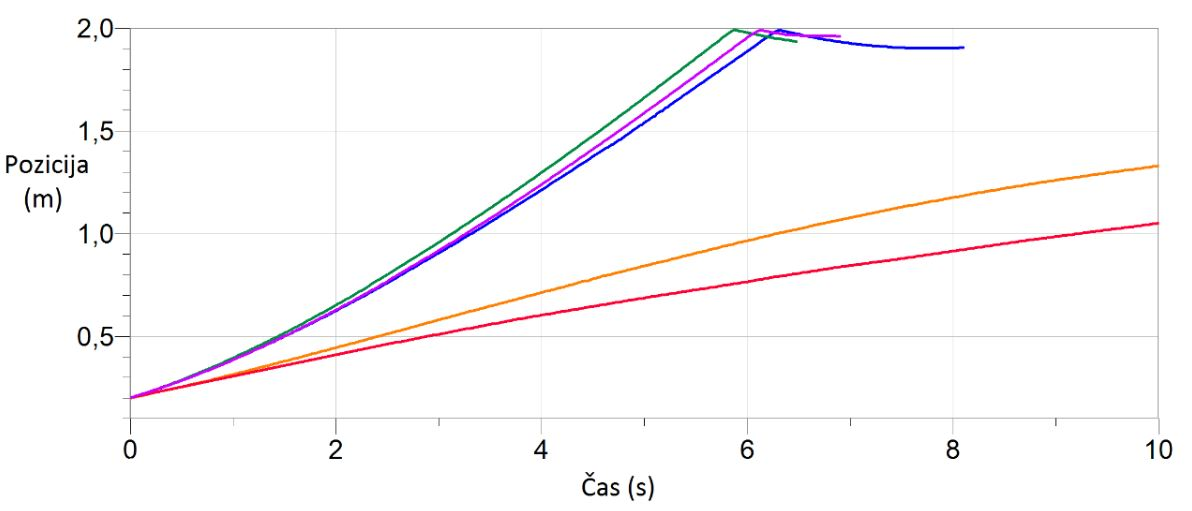
Slika št. 27: Graf –
primerjava hitrosti in pozicije vozička glede na oddaljenost magneta od klanca
vijolična krivulja – voziček brez magnetov
zelena krivulja – 1 magnet tik ob vozičku
oranžna krivulja – 1 magnet, s plastiko smo simulirali razdaljo 3 magnetov
od vozička
modra krivulja – 4 magneti tik ob vozičku
rdeča krivulja – 4 magneti, postavljeni drug na drugem
Zanimata nas le zelena in oranžna krivulja, saj se
navezujeta na zastavljeni cilj, da ugotovimo (ne)sorazmernost:
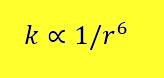
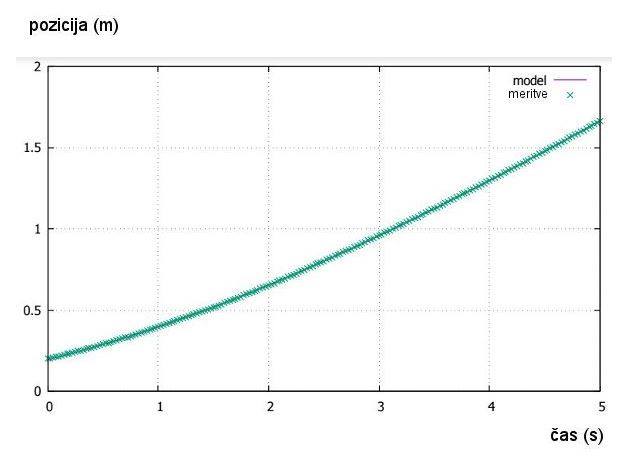
Slika št. 28: Graf –
prilagoditev (fit) krivulje meritvam pri vozičku z enim magnetom tik ob vozičku,
k1 = 0.1964 (zelena krivulja
na sliki št. 27)
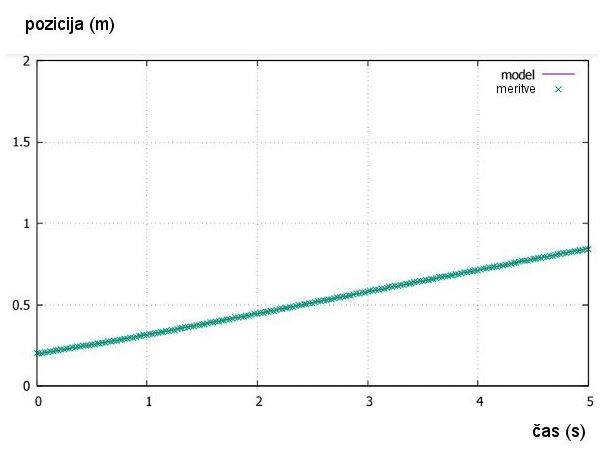
Slika št. 29: Graf –
prilagoditev (fit) krivulje meritvam pri vozičku z enim magnetom na razdalji 3
magnetov od vozička, k2 = 0.7253
(oranžna krivulja na sliki št. 27)
Za boljše razumevanje izračuna razdalje od magneta do aluminijastega
klanca, smo izdelali ustrezno sliko. 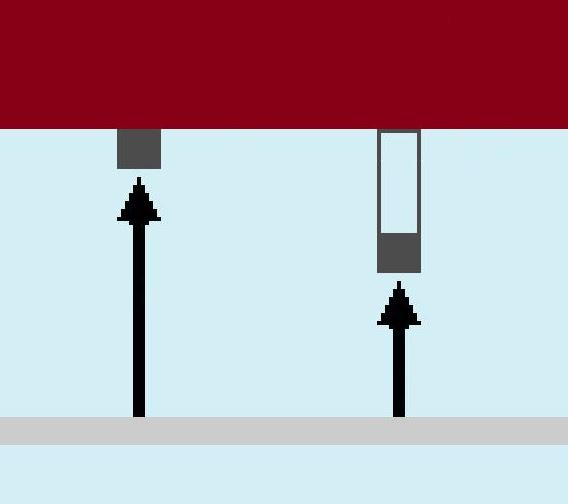
Slika št. 30: Prikaz
razdalje magneta tik ob vozičku do aluminijastega klanca (daljša puščica) in
razdalje magneta do aluminijastega klanca, ko smo med magnet in voziček dodali
plastiko (krajša puščica)
rdeča barva – voziček
svetlo siva barva – aluminijasti klanec
temno siva barva kvadratkov – magneta
Pri naslednjem izračunu bo daljša puščica r1, krajša puščica pa
r2.
Dobljeni vrednosti k sta bili: k1 = 0.1964 in k2 =
0.7253. 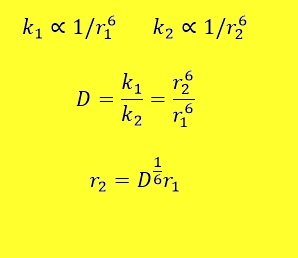
Vrednosti r1 in r2 ne poznamo. Vendar vemo, da je med
njima razdalja 3 magnetov, čemur ustreza dolžina 6 milimetrov. 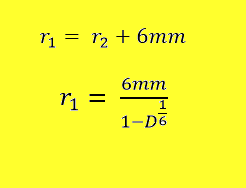
Vemo, da je r1 več kot 6mm in manj kot 10mm, saj je bilo pod
vozičkom prostora za maksimalno 4 magnete, postavljene drug na drugem. To
pomeni, da če bi bil rezultat med 6 in 10mm, bi teza o sorazmernosti verjetno
držala.
Rezultat, ki smo ga dobili, pa ne ustreza tej predpostavki, saj je r1
= 30.7mm. To pomeni, da je naša predpostavka ovržena. Možna razloga za tak
rezultat sta po našem mnenju lahko naslednja:
-s tem, ko se magnet približuje aluminijastemu klancu, se mogoče spreminja
efektivna površina magneta (A),
-ker magnet ni točkasti dipol, bi morali upoštevati še nekaj drugih
parametrov, ki delujejo na gostoto magnetnega polja (B).
Izpeljava
enačbe matematičnega modela
|